Длина программы в операторах

С использованием рассмотренных программных параметров можно получить уравнение для оценки количественного соотношения между длиной программы N и словарем  Это уравнение на первый взгляд может показаться несколько неожиданным Однако тщательный анализ доказывает его правомерность кроме этого его правильность подтверждается экспериментально

Строка длины N образуемая символами входящими в словарь из  символов должна подчиняться ряду ограничений Требование согласно которому каждый символ словаря должен появиться по меньшей мере хотя бы один раз гарантирует выполнение условия

что определяет нижнюю границу для N выраженную через 

Найдем верхнюю границу для N Разобьем строку длины N на подстроки длины  Разделенная таким образом программа для ЭВМ оказывается состоящей из N/ операторов длины  каждый Теперь если мы потребуем чтобы строка не содержала двух одинаковых подстрок длины  то появится искомая верхняя граница

Требование отсутствия дубликатов подстрок длины  является весьма обоснованным в программах для ЭВМ в которых экономия выражений приводит к тому что общему подвыражению дается отдельное имя поэтому его надо вычислять только один раз Следовательно если общее подвыражение длины  необходимо программе более одного раза присваивание его отдельному операнду увеличит  (число типов операторов) на единицу

Федеральная образовательная программа дошкольного образования

Число возможных комбинаций из  элементов взятых по  за раз хорошо известно из школьного курса математики и составляет

N    +1

Если учесть что операторы и операнды как правило, чередуются, то можно получить другое соотношение

N  1  1 2  2

Верхняя граница для этого неравенства должна включать не только упорядоченное множество из N элементов представляющих исследуемую программу но и его всевозможные подмножества Семейство всевозможных подмножеств из N элементов содержит 2 N элементов. Следовательно мы можем приравнять число возможных комбинаций из операторов и операндов (равное числу подстрок N/) числу подмножеств из N элементов и выразить длину реализации алгоритма через его словарь Из уравнения

2 N = 1  1 2  2

N = log2 (1  1 2  2 )

N = log2 1  1 + log2 2  2

Это дает нам уравнение оценки длины

1 log21 + 2 log22 (2.1)

В этом выражении символ N снабдили  для того чтобы отличать вычисленную (теоретическую) оценку длины от значения N полученного в результате непосредственного измерения (опытной длины) Эта оценка соответствует основным концепциям теории информации, по которым частота использования операторов и операндов в программе пропорциональна двоичному логарифму количества их типов. Выражение (2.1) представляет собой идеализированную аппроксимацию измеренной длины N=N1+N2 , справедливую для программ, не содержащих несовершенств (стилистических ошибок) [1]. Экспериментальные исследования ряда авторов на представительной группе программ показали, что для стилистически корректных программ отклонения в оценке их теоретической длины от опытной не превышают (10-15)% .

У-09. Федеральные образовательные программы НОО, ООО, СОО

Источник: studfile.net

Вычисление метрических характеристик основных процедур программы

Метрическими характеристиками программы или алгоритма называются соотношения, определяющие реализацию алгоритма. С помощью этих характеристик можно оценить алгоритм через внешние формы его проявления, независимо от языка программирования.

Практическое применение теория программометрики нашла в нормировании труда при серийном производстве, в оценивании времени разработки программы программистом (например, при принятии на работу), в оценивании количества ошибок в программе после ее написания и в других областях.

Если задана реализация алгоритма на каком-либо языке программирования, можно идентифицировать все операнды, определенные как переменные или константы, используемые в этой реализации, а также операторы, заданные в виде отдельных символов и их комбинаций, влияющие на значения и порядок операндов. Таким образом, мы получим словарь данной реализации, состоящий из простых операторов и операндов, используемых в программе, а по сумме всех операторов и операндов – длину реализации.

На основе словаря и длины реализации М.Х.Холстедом , [5], были получены метрические характеристики алгоритмов, пригодные для практического применения. Им также были введены следующие обозначения:

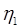
— число простых операторов;

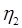
— число простых операндов;

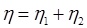
тогда — размер словаря. (6.1)

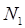
— общее число всех операторов, появляющихся в данной реализации;

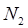— общее число всех операндов, появляющихся в данной реализации; тогда 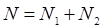— длина реализации. (6.2)

Введем некоторые требования на длину реализации 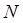: 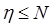, так как каждый символ словаря должен появиться в программе, по крайней мере, один раз –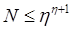

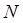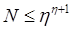нижняя граница для ; — верхняя граница.

Длина реализации по словарю определяется Холстедом таким образом:

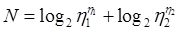
, (6.3)

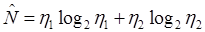
. (6.4)

Интерпретировать это уравнение можно по-разному. С одной стороны, это длина выражения любого алгоритма, а с другой – так как сумма двух логарифмов есть логарифм произведения, и первый множитель зависит от операторов, а второй от операндов, то длина может быть интерпретирована как двумерная величина, то есть как мера площади.

Важной характеристикой алгоритма является его размер, который меняется при переводе алгоритма с одного языка на другой, а также является различным для разных алгоритмов.

Соответствующая метрическая характеристика размера любой реализации какого-либо алгоритма, называемая объемом V, определяется как

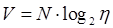, (6.5)

где 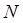— длина реализации, 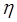— ее словарь. Эта формула дает выражение объема в битах.

Реализация алгоритма в наиболее сжатой, «идеальной» форме, предполагает существование такого языка, в котором требуемая операция уже определена или реализована, возможно, в виде процедуры или функции. Таким образом, для реализации алгоритма на таком языке необходимы лишь имена операндов для его аргументов и результатов.

Введем следующие обозначения для параметров этого «минимального» языка:

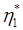— минимально возможное число простых операторов; 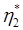— минимально возможное число простых операндов, которое равно сумме входных и выходных параметров;

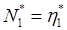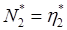, , (6.6)

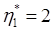
так как в минимальной форме ни операторы, ни операнды не требуют повторений. Минимально возможное число операторов для любого алгоритма , так как каждый алгоритм должен включать один оператор для имени функции и один в качестве символа присваивания или группировки. Тогда выражение для потенциального объема имеет вид:

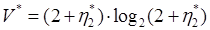
. (6.7)

Зная объем программы и ее потенциальный объем, можно определить уровень программы :

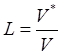
. (6.8)

Очевидно, с увеличением объема уровень программы уменьшается, и наоборот.

Если требуется определить уровень программы непосредственно из реализации, не зная чему равен ее потенциальный объем, используют следующую формулу для оценки уровня языка:

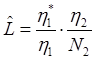
. (6.9)

Можно вычислить также коэффициент интеллектуального содержания программы, воспользовавшись следующей формулой:

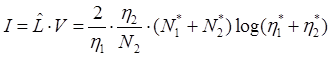
. (6.10)

Этот коэффициент определяет количество информации в алгоритме.

Холстед ввел такое понятие как число элементарных мысленных различений, требуемых для порождения программы, а на его основе – понятие работы E. Если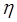

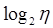— число элементов в словаре, то — элементарное мысленное сравнение, необходимое для выбора одного слова, а величину 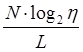Холстед определяет как элементарное мысленное сравнение. Работу по программированию можно представить в виде:

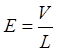
, (6.11)

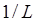
где объем V равен числу мысленных сравнений, а — среднее число элементарных мысленных различений, входящих в каждое мысленное сравнение. Если подставить формулу (6.8) в уравнение (6.11) получим:

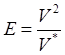
, (6.12) что мысленная работа по реализации алгоритма с данным потенциальным объемом в каждом языке пропорциональна квадрату объема программы.

Можно преобразовать уравнение (6.11) таким образом, чтобы работа по реализации алгоритма выражалась в единицах времени. Для этого разделим обе части уравнения на число различений в единицу времени. Считается, что в среднем человек способен примерно на 15-20 мысленных различений в секунду, и это число обозначают как S, S=18 (число Страуда). Таким образом, выражение для времени написания программы имеет вид:

Источник: vunivere.ru

Большая Энциклопедия Нефти и Газа

Длина программы , производящей хаотическую последовательность, должна быть близка к длине последней. Итак, простые последовательности — это те, которые порождаются короткими программами. Изложим эти интуитивные соображения несколько более формально. [1]

Длины программ функций из этих множеств равны соответственно п2 и Пз. Искомый нумератор Н определим как композицию этих множеств: Я. Длина программ функций из Я не превышает суммы длин программ функций из F, Gait и Gali. Вычисления отображений из Я на словах из А проводятся так же, как и в ранее разобранных случаях, и требуют А ( log А) 2 -операций. [2]

Длина программы экспоненциального фильтра , по-видимому, меньше, чем программы любого усредняющего фильтра, поскольку здесь не требуется счет. Время выполнения программы также меньше, поскольку здесь нужны только два действия сложения и одно умножение. Эти преимущества при программировании, а также меньший фазовый сдвиг определяют популярность экспоненциального фильтра в АСУ ТП. [3]

Длину программы , содержащую последовательность из п одинаковых фрагментов, можно сократить, охватив один из таких фрагментов циклом, вычисления в котором повторяются п раз. В программах на алгоритмических языках для этой цели можно использовать как операторы цикла общего вида: пока Сусловие, выполнять Стело иикла или повторять Стело цикла, пока Сусловие, так и специализированные операторы цикла вида для / п до 1 выполнить тело цикла -, где телом цикла является многократно выполняемый фрагмент программы. [4]

Длину программы на компактном входном языке можно сократить, рационально используя возможные разнообразные способы реализации одних и тех же операторов алгоритма. Следует учитывать, что уменьшение длины программы складывается из небольших уменьшений числа шагов в отдельных фрагментах, а если длина оптимизируемой программы лишь на несколько шагов превышает число ячеек программной памяти, выигрыш от сокращения длины программы и устранения необходимости использования пакета программы оказывается значительным. Если при уменьшении длины отдельных фрагментов удается устранить и операторы безусловных переходов ( что соответствует требованиям структурирования программ), то заметно сократится и время выполнения программы. [5]

Длину программы иногда можно сократить заменой линейных участков циклическими, которые, естественно, исполняются дольше, поскольку требуется выполнять дополнительные команды управления циклами. Аналогично объем используемой памяти в некоторых случаях можно сократить за счет применения более сложных и, следовательно, дольше исполняемых алгоритмов. Однако бывают случаи, когда программа содержит избыточные команды, устранение которых сокращает и ее длину, и время исполнения. [6]

С увеличением длины программы все труднее становится запомнить коды различных операций. Некоторую помощь в этом отношении оказывают мнемонические обозначения ( см. гл. [7]

Если сокращение длины программы , рассмотренное в предыдущей главе, носило, так сказать, показательный характер и преследовало цель улучшить программу, то при составлении программы в этой главе оно стало суровой необходимостью. [8]

Это увеличивает длину программ и время обработки текстов. Чтобы исключить эти негативные явления, в ЭВМ общего назначения текстовая информация представляется в формате (2.10) и в систему команд вводятся специальные операции для обработки строк символов. [10]

XN) — длина кратчайшей программы , которая получает эту последовательность на машине Тьюринга. [11]

Основными средствами минимизации длины программы , предусмотренными практически во всех входных языках, являются обращения к подпрограммам и организация циклов. Если в программе несколько одинаковых процедур, то целесообразно вынести один фрагмент с такой процедурой в подпрограмму, оканчивающуюся оператором возврата из подпрограммы, а на месте фрагментов в исходной программе записать операторы обращения к подпрограмме. Так как время выполнения подпрограмм возрастает за счет затрат времени на переходы, то организация обращений к подпрограммам оказывается целесообразной лишь при допустимом увеличении времени счета и только в том случае, если введение подпрограмм уменьшает общую длину программы. [12]

Использование подпрограммы сокращает длину программы . Блок, символизирующий команду Переход к подпрограмме, является точкой передачи управления подпрограмме. Блок-схема алгоритма подпрограммы начинается блоком Вход, за которым следуют блоки присвоения переменной Y значения X2, переменной Z значения V2X2, вывода на печать значений X и Y, а также X и Z. Завершает блок-схему блок Возврат, обозначающий возврат управления в ту точку программы, из которой происходило обращение к подпрограмме, т.е. на вход блока, расположенного после блока Переход к подпрограмме. На рис. 5.9 схематически изображено семикратное обращение к подпрограмме в процессе выполнения главной программы. [14]

По меньшей мере от длины программы прямо зависит время, затрачиваемое на передачу программы между оперативной и внешней памятью при переключении ее активности. [15]

Источник: www.ngpedia.ru