Длина программы метрики холстеда

В 1987 г. было утверждено пять международных стандартов ISO (International Organization for Standardization), устанавливающих требования к системам обеспечения качества про­дукции на предприятиях:

1) «Стандарты по управлению качеством и обеспечению качества. Руководство для выбора и применения» (ISO 9000);

2) «Система качества. Модели обеспечения качества при проек­тировании, разработке, производстве, монтаже и обслуживании» (ISO 900S);

3) «Система качества. Модели обеспечения качества при про­изводстве и монтаже» (ISO 9002);

4) «Система качества. Модели обеспе­чения качества в процессе контроля и испытания готовой продукции» (ISO 9003);

5) «Управление качеством и элементы системы качества. Ос­новные направления» (ISO 9004).

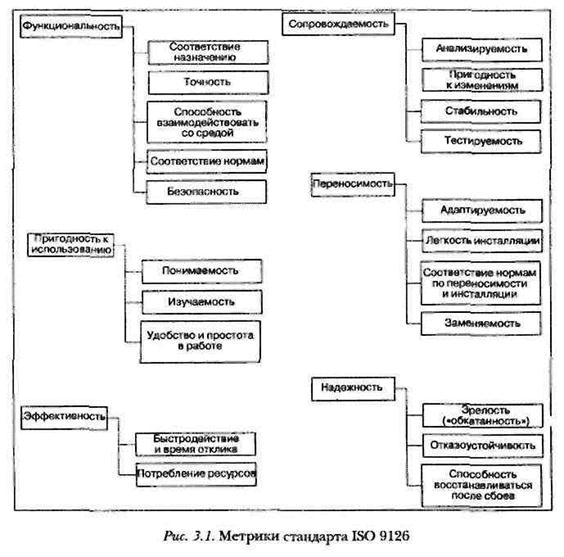
Метрика программного обеспечения – это мера, позволяющая получить численное значение некоторого свойства программного обеспечения или его спецификаций.

ПРОДУКТ в IT. Как рассчитать основные метрики? Просто о сложных формулах

Метрики принято разделять на три основные группы:

1. метрики размера программ;
2. метрики сложности потока управления программ;
3. метрики сложности потока данных программ.

Характеристикой раз­мера программ является количество строк исходного текста. При этом под строкой понимается любой оператор программы. Оценка размера программы недостаточна для принятия решения о ее сложности, но вполне применима для классификации программ, существенно раз­личающихся объемами.

Метрика Холстеда. Основу метрики Холстеда составляют четыре измеряемые характеристики программы:

— число уникальных операторов программы, включая символы-

разделители, имена процедур и знаки операций;

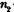
—число уникальных операндов программы;

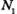
— общее число операторов в программе;

— общее число операндов в программе.

С учетом этих характеристик, получаемых непосредственно при ана­лизе исходных текстов программ, были введены следующие оценки:

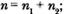
1) словарь программы – это словарный запас, необходимый для написания программы, с уче­том того, что необходимая функция уже реализована в данном языке и, следовательно, программа сводится к вызову этой функции:

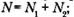
2) длина программы:

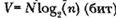
3) объем программы: .

Здесь под битом подразумевается логическая единица информа­ции — символ, оператор, операнд.

Источник: studopedia.su

МЕТРИКА ПОДСЧЕТА ТОЧЕК ПЕРЕСЕЧЕНИЯ.

Оценки первой группы наиболее просты и, очевидно, поэтому получили широкое распространение. Традиционной характеристикой размера программ является количество строк исходного текста. Под строкой понимается любой оператор программы, поскольку именно оператор, а не отдельно взятая строка является тем интеллектуальным «квантом» программы, опираясь на который можно строить метрики сложности ее создания.

Лекция №2. Метрики качества программного обеспечения

Непосредственное измерение размера программы, несмотря на свою простоту, дает хорошие результаты. Конечно, оценка размера программы недостаточна для принятия решения о ее сложности, но вполне применима для классификации программ, существенно различающихся объемами. При уменьшении различий в объеме программ на первый план выдвигаются оценки других факторов, оказывающих влияние на сложность. Таким образом, оценка размера программы есть оценка по номинальной шкале, на основе которой определяются только категории программ без уточнения оценки для каждой категории.

К группе оценок размера программ можно отнести также и метрику Холстеда.

МЕТРИКА ХОЛСТЕДА.

Основу метрики Холстеда составляют четыре измеряемых характеристики программы:

n1 — число уникальных операторов программы, включая символы-

разделители, имена процедур и знаки операций (словарь операторов);

n2 — число уникальных операндов программы (словарь операндов);

N1 — общее число операторов в программе;

N2 — общее число операндов в программе.

Опираясь на эти характеристики, получаемые непосредственно при анализе исходных текстов программ, М. Холстед вводит следующие оценки:

Под битом подразумевается логическая единица информации — символ, оператор, операнд.

Далее М. Холстед вводит n* — теоретический словарь программы, т.е. словарный запас, необходимый для написания программы, с учетом того, что необходимая функция уже реализована в данном языке и, следовательно, программа сводится к вызову этой функции. Например, согласно М. Холстеду, возможное осуществление процедуры выделения простого числа могло бы выглядеть так:

где Y — массив численных значений, содержащий искомое число X.

Теоретический словарь в этом случае будет состоять из

а его длина, определяемая как

будет равняться 4.

Используя n*, Холстед вводит оценку V*:

с помощью которой описывается потенциальный объем программы, соответствующий максимально компактному тексту программы, реализующей данный алгоритм.

МЕТРИКИ СЛОЖНОСТИ ПОТОКА УПРАВЛЕНИЯ ПРОГРАММ.

Вторая наиболее представительная группа оценок сложности программ — метрики сложности потока управления программ. Как правило, с помощью этих оценок оперируют либо плотностью управляющих переходов внутри программ, либо взаимосвязями этих переходов.

И в том и в другом случае стало традиционным представление программ в виде управляющего ориентированного графа G=(V,E), где V — вершины, соответствующие операторам, а E — дуги, соответствующие переходам.

МЕТРИКА МАККЕЙБА.

Впервые графическое представление программ было предложено Маккейбом. Основной метрикой сложности он предлагает считать цикломатическую сложность графа программы, или, как ее еще называют, цикломатическое число Маккейба, характеризующее трудоемкость тестирования программы.

Для вычисления цикломатического числа Маккейба Z(G) применяется формула

где e — число дуг ориентированного графа G;

v — число вершин;

p — число компонентов связности графа.

Число компонентов связности графа можно рассматривать как количество дуг, которые необходимо добавить для преобразования графа в сильно связный. Cильно связным называется граф, любые две вершины которого взаимно достижимы. Для графов корректных программ, т. е. графов, не имеющих недостижимых от точки входа участков и «висячих» точек входа и выхода, сильно связный граф, как правило, получается путем замыкания дугой вершины, обозначающей конец программы, на вершину, обозначающую точку входа в эту программу.

По сути Z(G) определяет число линейно независимых контуров в Сильно связном графе. Иначе говоря, цикломатическое число Маккейба показывает требуемое количество проходов для покрытия всех контуров сильно связного графа или количество тестовых прогонов программы, необходимых для исчерпывающего тестирования по критерию «работает каждая ветвь».

Для программы, граф которой изображен на рис.1, цикломатическое число при e=10, v=8, p=1 определится как Z(G)=10-8+2=4.

Цикломатическое число зависит только от количества предикатов, сложность которых при этом не учитывается. Например, имеется два оператора условия:

Оба оператора предполагают единственное ветвление и могут быть представлены одним и тем же графом (рис. 2). Очевидно, цикломатическое число будет для обоих операторов одинаковым, не отражающим сложности предикатов, что весьма существенно при оценке программ.

МЕТРИКА МАЙЕРСА.

Исходя из этого Г. Майерс предложил расширение этой метрики. Суть подхода Г. Майерса состоит в представлении метрики сложности программ в виде интервала [Z(G), Z(G)+h]. Для простого предиката h=0, а для n-местных предикатов h=n-1. Таким образом, первому оператору соответствует интервал [2,2], а второму — [2,6].

По идее такая метрика позволяет различать программы, представленные одинаковыми графами. К сожалению, информация о результатах использования этого метода отсутствует, поэтому ничего нельзя сказать о его применимости.

МЕТРИКА ПОДСЧЕТА ТОЧЕК ПЕРЕСЕЧЕНИЯ.

Рассмотрим метрику сложности программ, получившую название «подсчет точек пересечения», авторами которой являются М. Вудвард, М. Хенел и Д. Хидлей. Метрика ориентирована на анализ программ, при создании которых использовалось неструктурное кодирование на таких языках, как язык ассемблера и Фортран.

В графе программы, где каждому оператору соответствует вершина, т. е. не исключены линейные участки, при передаче управления от вершины a к b номер оператора a равен min(a,b), а номер оператора b — max(a,b). Точка пересечения дуг появляется, если

Иными словами, точка пересечения дуг возникает в случае выхода управления за пределы пары вершин (a,b) (рис. 3).

Количество точек пересечения дуг графа программы дает характеристику не структурированности программы.

МЕТРИКА ДЖИЛБА.

Одной из наиболее простых, но, как показывает практика, достаточно эффективных оценок сложности программ является метрика Т. Джилба, в которой логическая сложность программы определяется как насыщенность программы выражениями типа IF-THEN-ELSE. При этом вводятся две характеристики: CL — абсолютная сложность программы, характеризующаяся количеством операторов условия; cl — относительная сложность программы, характеризующаяся насыщенностью программы операторами условия, т. е. cl определяется как отношение CL к общему числу операторов.

Используя метрику Джилба, мы дополнили ее еще одной составляющей, а именно характеристикой максимального уровня вложенности оператора CLI, что позволило не только уточнить анализ по операторам типа IF-THEN-ELSE, но и успешно применить метрику Джилба к анализу циклических конструкций.

МЕТРИКА ГРАНИЧНЫХ ЗНАЧЕНИЙ

Большой интерес представляет оценка сложности программ по методу граничных значений.

Введем несколько дополнительных понятий, связанных с графом программы.

Пусть G=(V,E) — ориентированный граф программы с единственной начальной и единственной конечной вершинами. В этом графе число входящих вершин у дуг называется отрицательной степенью вершины, а число исходящих из вершины дуг — положительной степенью вершины. Тогда набор вершин графа можно разбить на две группы : вершины, у которых положительная степень =2.

Вершины первой группы назовем принимающими вершинами, а вершины второй группы — вершинами отбора.

Для получения оценки по методу граничных значений необходимо разбить граф G на максимальное число подграфов G’, удовлетворяющих следующим условиям : вход в подграф осуществляется только через вершину отбора; каждый подграф включает вершину (называемую в дальнейшем нижней границей подграфа), в которую можно попасть из любой другой вершины подграфа. Например, вершина отбора, соединенная сама с собой дугой-петлей, образует подграф. (рис. 4, таблица 1).

Число вершин, образующих такой подграф, равно скорректированной сложности вершины отбора (таблица 2). Каждая принимающая вершина имеет скорректированную сложность, равную 1, кроме конечной вершины, скорректированная сложность которой равна 0. Скорректированные сложности всех вершин графа G суммируются, образуя абсолютную граничную сложность программы. После этого определяется относительная граничная сложность программы :

где S0 — относительная граничная сложность программы; Sa — абсолютная граничная сложность программы; v — общее число вершин графа программы.

Дата добавления: 2021-12-10 ; просмотров: 125 ; Мы поможем в написании вашей работы!

Источник: studopedia.net

Метрики, основанные на лексическом анализе программ. Метрики Холстера

ОСОБЕННОСТИ ФОРМИРОВАНИЯ
СЛОВАРЯ ПРОГРАММЫ
Любая программа определяет последовательность
действий над операндами с помощью операторов.
Исходный текст программы, записываемой на том
или ином языке программирования представляет
собой набор текстовых строк, которые записываются
по специальным правилам, и в том числе имеет
свои элементы. Операнд – это некоторый объект или
величина, обрабатываемая в программе, а
оператор представляет собой обозначение
конкретного действия, выполняемого по отношению к
операнду.

3.

Если считать, что словарь любой программы состоит только из имен операторов
и операндов, то тексты программ всегда удовлетворяют следующим условиям:
• маловероятно появление какого-либо имени оператора или операнда много
раз подряд – языки программирования, как правило, позволяют создавать такие
конструкции, в которых подобные фрагменты программы имеют минимальную
длину;
• циклическая организация программ исключает многократное повторение какойлибо группы операторов и операндов – более компактные варианты текстов
получаются при разумном использовании развитых возможностей языков
программирования, причем многообразие языков предоставляет богатую палитру
инструментов;
• блоки программ, требующие периодического повторения при ее исполнении,
обычно оформляются как процедуры или функции, поэтому в текстах программ
достаточно применения только их имен;
• имя каждого операнда должно появляться в тексте программы хотя бы один раз –
многие среды программирования обращают внимание программистов на
неиспользуемые имена, которые следует удалять из текста программ, чтобы
сократить объем памяти, используемой при объявлении переменных.

4.

СХЕМАТИЧНО ЭТИ УСЛОВИЯ,
ОТНОСЯЩИЕСЯ К ТЕКСТУ ПРОГРАММ,
ОТОБРАЖЕНЫ НА РИС.

5.

ИЗМЕРЯЕМЫЕ СВОЙСТВА
ПРОГРАММ
В состав измеримых свойств любого представления алгоритма (или
программы) могут быть включены следующие метрические характеристики:
• η1 – число простых (уникальных) операторов, появляющихся в данной
реализации;
• η2 – число простых (уникальных) операндов, появляющихся в данной
реализации;
• N1 – общее число всех операторов, появляющихся в данной реализации;
• N2 – общее число всех операндов, появляющихся в данной реализации;
• f1j – число появлений в программе j-го оператора, где j = 1, 2, 3, . η1;
• f2j – число появлений в программе j-го операнда, где j = 1, 2, 3, . η2

6.

η2.
Учитывая эти основные метрические характеристики для
программы, в конкретной реализации текста программы
можно определить:
• словарь η = η1 + η2;
• длину реализации программы N = N1 + N2;
• длину программы Ñ = (η1 · log2 η1) + (η2 · log2 η2).

7.

МЕТРИКИ ХОЛСТЕДА:
вычисляются
на основании
анализа числа строк и
синтаксических элементов
исходного кода программы

8.

М.
Холстед вводит аппроксимирующую формулу
для измерения теоретической длины программы N^
N^ = n1*log2(n1) + n2*log2(n2), (10)
где n1 — словарь операторов;
n2 — словарь операндов программы.

9.

Вводя
эту оценку, Холстед исходит из основных концепций теории
информации, по аналогии с которыми частота использования операторов
и операндов в программе пропорциональна двоичному логарифму
количества их типов. Таким образом, выражение (10) представляет собой
идеализированную аппроксимацию (1), т. е. справедливо для
потенциально корректных программ, свободных от избыточности или
несовершенств (стилистических ошибок). Несовершенствами можно
считать следующие ситуации:
— последующая операция уничтожает результаты предыдущей без их
использования;
— присутствуют тождественные выражения, решающие совершенно
одинаковые задачи;
— одной и той же переменной назначаются различные имена и т. п.

10.

Подобные
ситуации приводят к изменению N без изменения
n.
М.
Холстед утверждает, что для стилистически корректных
программ отклонение в оценке теоретической длины N^ от
реальной N не превышает 10%.
Значение
N^ может быть использовано как эталонное
значение длины программы со словарем n. Длина корректно
составленной программы N, т. е. программы, свободной от
избыточности и имеющей словарь n, не должна отклоняться
от теоретической длины программы N^ более чем на 10%.
Таким образом, измеряя n1, n2, N1 и N2 и сопоставляя
значения N и N^ для некоторой программы, при более чем
10%-ном отклонении можно говорить о наличии в программе
стилистических ошибок, т. е. несовершенств.

11.

На
М.
практике N и N^ часто существенно различаются.
Холстед вводит n* — теоретический словарь программы,
т.е. словарный запас, необходимый для написания
программы, с учетом того, что необходимая функция уже
реализована в данном языке и, следовательно, программа
сводится к вызову этой функции. Например, согласно М.
Холстеду, возможное осуществление процедуры выделения
простого числа могло бы выглядеть так:

12.

CALL
SIMPLE (X,Y),
где
Y — массив численных значений, содержащий искомое
число X.
Теоретический
словарь в этом случае будет состоять из
n1*
: , n1*=2;
n2*
: , n2*=2,
а
его длина, определяемая как
n*
= n1* + n2*,
будет
равняться 4.
Используя
V*
n* , Холстед вводит оценку V*
= n* * log2 n*, (11)

13.

МЕТРИКИ ХОЛСТЕДА
Основу
метрики Холстеда составляют четыре измеряемые
характеристики программы:
NUOprtr
(Number of Unique Operators) — число уникальных
операторов программы, включая символыразделители, имена
процедур и знаки операций (словарь операторов);
NUOprnd
(Number of Unique Operands) — число уникальных
операндов программы (словарь операндов);
Noprtr
(Number of Operators) — общее число операторов в
программе;
Noprnd
(Number of Operands) — общее число операндов в
программе.

14.

ОЦЕНКИ НА ОСНОВЕ МЕТРИКИ
ХОЛСТЕДА
Словарь программы (Halstead Program Vocabulary):
HPVoc = NUOprtr + NUOprnd;
Длина программы (Halstead Program Length):
HPLen = Noprtr + Noprnd;
Объем программы (Halstead Program Volume):
HPVol = HPLen log2 HPVoc;
Сложность программы (Halstead Difficulty, HDiff):
HDiff = (NUOprtr/2) × (NOprnd / NUOprnd);
На основе показателя HDiff предлагается оценивать усилия программиста при
разработке при помощи показателя HEff (Halstead Effort):
HEff = HDiff × HPVol.

15.

Также
на основе показателя HDiff имеется
возможность оценивать усилия программиста
при разработке при помощи показателя HEff
(Halstead Effort): HEff= HDiff x HPVol.

16.

МЕТРИКИ СЛОЖНОСТИ ПОТОКА УПРАВЛЕНИЯ
ПО
Метрики
второй группы базируются на анализе управляющего
графа программы. Управляющий граф G(V, Е) строится в виде
ориентированного графа, в котором вычислительные операторы
или выражения представляются в виде вершин V(Vh . Vm), а
передача управления между вершинами — в виде
ребер Е(ЕХ,Еп). Как правило, на основании анализа данного
графа строят метрики для оценки количества управляющих
переходов внутри программ, либо взаимосвязями этих переходов.

Источник: ppt-online.org