Сетевой метод. Позволяет определить минимальную, максимальную и среднюю трудоемкость.
Перед расчётом производится нумерация вершин ГСА по номерам 0,1,2. К; где 0 и к соответственно номера начальной и конечной вершин. Затем выделяются циклы по рангам 1,2. Для цикла m с низшим рангом находится среднее число повторений ‘ ‘ на один прогон алгоритма
где — вероятность перехода по дуге, замыкающей цикл по вершинам к и /. Затем определяется среднее время выполнения операторов тела цикла , для чего находится среднее число обращений к вершинам i этого тела
где z — множество номеров вершин, предшествующих номеру i, -вероятности обращений из вершин j в вершину i. После определения всех определяется
где R — множество номеров вершин цикла m; — средние времена выполнения операций в вершине i (см. (2.1 + 2.3)). Для цикла определяется среднее время выполнения
И цикл заменяется эквивалентным оператором со средним временем выполнения .
Повторяя процедуру для всех циклов последовательно по рангам и заменяя их эквивалентными операторами, в последующем находится среднее время выполнения алгоритма.
Вычислительная сложность алгоритма
Аналогично определяется минимальное и максимальное время выполнения. Для этого находятся минимальное и максимальное время цикла с номером m последовательно по рангам с заменой их эквивалентными операторами с временами и . Здесь и — минимальное и максимальное время выполнения тела цикла m; и — минимальное и максимальное число повторений цикла.
Времена и находятся по формулам
Здесь и — времена выполнения операторов начальной вершины; и — минимальное и максимальное время на момент окончания выполнения операторов i -ой вершины; (j,i) — дуга из вершины j в вершину i; Dm -множество дуг; к — номер конечной вершины цикла; времена и ; выбираются по отношению ко всем вершинам j, связанными выходами с вершиной i; и — минимальное и максимальное время выполнения операторов в вершине i.
Трудоемкость алгоритма – это объем работы, которое необходимо выполнить. Для его реализации она может быть измерена в числе тактов, количестве команд и т.д.
Существует сетевой метод оценки трудоемкости, который основан на описании алгоритма в виде граф — схемы алгоритма (ГСА).
ГСА состоит из операторных вершин, связанных между собой дугами переходов. Вершины делятся на 3 типа (начальная, конечная и функциональная). Начальная и конечная имеют нулевую трудоемкость. Функциональные содержат перечень операций соответствующие данному алгоритму. Делятся на 2 вида:
1) вершины реализации процессорных операций,
2) вершины реализации ввода-вывода или операции передачи информации. Для общей оценки должна быть известна трудоемкость каждого оператора.
V – множество операторных вершин, где V0 и Vn – начальная и конечные вершины.
Каждая вершина характеризуется средним числом обращений – ni, где . Вершина характеризуется объем работ для выполнения операции i-ой вершины. V0=VK=0 Матрица характеризует вероятность перехода из i-ой в j-ю. Перед расчетом граф-схемы алгоритма с циклами производят ранжирование. К циклам I – го ранга относятся циклы, не содержащие других циклов.
Python — Полный Курс по Python [10 ЧАСОВ]
Циклы II- го ранга включают в себя только циклы I-го ранга. Суть заключается в определении трудоемкости тела цикла и с учетом числа повторений находится трудоемкость всего цикла этого ранга. Определенный цикл заменяется эквивалентным оператором.
Пусть даны циклы разных рангов:
где Q — суммарная трудоемкость всего алгоритма.
У каждого из этих циклов есть трудоемкость и среднее число повторений циклов i-го ранга.
где n i – среднее число повторений циклов i- го ранга,
t I трудоемкость тела цикла
где Pkl – вероятность перехода по дуге обратного перехода
— трудоемкость тела цикла
Среднее число обращений
где r – множество операторов, из которых происходит обращение в данную вершину Pji.
Вероятность обращения из j-й в i-ую. nj – число обращения к j-той вершине за одну реализацию алгоритма.
1. Что такое граф-схема алгоритма?
2. В чем определяется трудоемкость алгоритма?
3. В чем суть сетевого метода расчета трудоёмкости алгоритма?
4. Что такое ранг цикла?
5. Как формализовано, определяется число повторений цикла?
Источник: megalektsii.ru
Сравнение алгоритмов на основе функции трудоемкости
Итак, под трудоемкостью алгоритма для данной конкретной проблемы, заданной множеством D, понимают количество элементарных операций, задаваемых алгоритмом в принятой модели вычислений. В качестве модели вычислений рассматривают абстрактную машину, имеющую процессор с фон- Неймановской архитектурой, адресную память и набор элементарных операций, соответствующий языкам высокого уровня. Такая модель вычислений называется машиной с произвольным доступом к памяти (RAM).
Функция трудоемкости fA (D) – это отношение, которое связывает входные данные с количеством элементарных операций. Значением этой функции является целое положительное число.
Опыт показывает, что количество элементарных операций, задаваемых алгоритмом, то есть значение fA (D) на входе длины n, где n=|D|, не всегда совпадает с количеством операций на другом входе такой же длины. (потому что существует много множеств D длины n – то есть может быть много различных входных наборов данных)
Поэтому при анализе алгоритмов различают худший случай, лучший случай, и средний случай.
Худший случай – это наибольшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.
Лучший случай – это наименьшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.
Средний случай – среднее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.
Для получения значений функции трудоемкости fA (D) определили элементарные операции, используемые в языках высокого уровня, которые необходимо учитывать при расчетах.
Такими операциями являются:
Операция присваивание: а = b;
Одномерная индексация a[i]: (адрес (a)+i*длина элемента);
Операции сравнения: a < b;
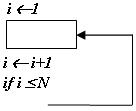
Конструкция «Следование» Трудоемкость конструкции есть сумма трудоемкостей блоков, следующих друг за другом, где k – количество блоков.
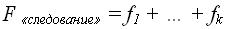
if(условие) then (блок с трудоемкостью fthen и вероятностью p)
else (блок с трудоемкостью felse и вероятностью (1-p)
Общая трудоемкость конструкции «Ветвление» требует анализа вероятности выполнения переходов на блоки «then» и «else» и определяется как:
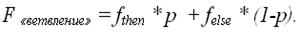
К этому придется еще добавить трудоемкость вычисления условия.
Для анализа худшего случая выбирается тот блок ветвления, который имеет большую трудоемкость, а для лучшего – тот, трудоемкость которого минимальна.
Общая трудоемкость определяется как
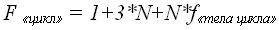
Примеры анализа трудоемкости алгоритмов.
Пример 1 Задача суммирования элементов квадратной матрицы
Sum =0 // 1 операция
For i = 1 to n // 3 операции на один проход цикла
For j = 1 to n // 3 операции на один проход цикла
Sum =Sum + A[i,j] // 4 операции
Алгоритм выполняет одинаковое количество операций при фиксированном значении n, и, следовательно, является количественно-зависимым. Его функция трудоемкости зависит только от размерности конкретного входа. Применение методики анализа конструкции «Цикл» дает:
fA(n)=1+1+ n *(3+1+ n *(3+4))=7*n 2 +4* n +2 = (n 2 ),
где внутренний цикл: f1(n) = 1+3*n+4*n
замечание по задаче:
под n понимается линейная размерность матрицы, в то время как на вход алгоритма подается n 2 значений.
Общее замечание:
Количественно-зависимые по трудоемкости алгоритмы — это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:
К ним можно отнести алгоритмы для стандартных операций с массивами и матрицами – умножение матриц, умножение матрицы на вектор и т.д.
Пример 2 Задача поиска максимума в массиве
Max = S[1] // 2 операции
For i = 2 to n // 3 операции на один проход цикла
then Max =S[i] // 2 операции
Алгоритмы обработки данных
Аннотация: В лекции рассматривается понятие ресурсной эффективности алгоритмов посредством анализа асимптотических функций временной и емкостной сложности, приводится классификация алгоритмов на основе функции временной сложности, рассматриваются общие методы оценки трудоемкости алгоритмов.
Цель лекции: изучить понятие и классификации алгоритмов обработки данных, трудоемкости алгоритмов и методов ее оценки, научиться выработке критериев и оценке трудоемкости алгоритмов с учетом критериев на примере реализаций и задач на языке C++.
Понятие «алгоритм обработки данных» в компьютерных науках используется для описания метода решения задачи, который в дальнейшем возможно реализовать в выбранной среде программирования. Тщательная разработка алгоритма является весьма эффективной частью процесса решения задачи в любой области применения. При разработке алгоритма для реальной задачи значительные усилия должны быть потрачены на осознание степени ее сложности, выяснение ограничений на входные данные , разбиение задачи на менее трудоемкие подзадачи.
Алгоритм не должен быть привязан к конкретной реализации. В силу разнообразия используемых средств программирования, их требований к аппаратным ресурсам и платформенной зависимости сходные по структуре, но различные в реализации, алгоритмы могут выдавать отличающиеся по эффективности результаты.
При этом некоторые среды программирования содержат встроенные библиотечные функции, реализующие базовые алгоритмы обработки данных (например, в MS Visual Studio 2010 в библиотеки С++ входит функция быстрой сортировки массивов данных). Чтобы решения были переносимыми и оставались актуальными, не рекомендуется их ориентировать на процедурную реализацию среды. Поэтому главным в рассматриваемом подходе является выбор метода решения с учетом специфики задачи. Адаптация к среде осуществляется позднее.
Выбор того или иного метода обработки данных определяется не только сложностью задачи. Учитывать необходимо и массовость применения разработанного кода: при однократном или редком обращении к реализации предпочтительнее бывают простые алгоритмы, которые несложны в разработке. При этом, однако, допускается возможным увеличение времени работы программы.
Массовое использование алгоритмов обработки данных требует поиска наилучшего алгоритма решения. Такой процесс бывает весьма сложен, так как требует выработки критериев оценки и применения математических методов для получения количественных характеристик. Направление компьютерных наук, занимающееся изучением оценки эффективности алгоритмов , называется анализом алгоритмов.
Ресурсная эффективность алгоритмов
Определение ресурсной эффективности алгоритмов – необходимая составляющая этапа анализа разработанного программного обеспечения. Повышение ресурсной эффективности вычислительных алгоритмов актуально при обработке больших объемов данных, когда аппаратных и/или программных ресурсов может быть недостаточно для корректного завершения работы программного кода.
Наиболее значимыми характеристиками ресурсной эффективности алгоритмов являются оценки временной и емкостной сложности , отражающие ресурсы процессора, оперативной памяти, а также внешних носителей данных (при использовании).
Под трудоемкостью алгоритма А на входе D будем понимать количество элементарных операций, которые учитываются при анализе алгоритма. Под худшим случаем трудоемкости понимают наибольшее количество операций, задаваемых алгоритмом А на всех входах D определенной размерности n . Определим лучший случай трудоемкости, как наименьшее количество операций в аналогичном алгоритме и при той же размерности входа. Средний случай трудоемкости определяется средним количеством операций рассматриваемого алгоритма и входных данных. Зависимость трудоемкости алгоритма А от значения параметров на входе D определяет функцию трудоемкости алгоритма А для входа D .
Классический анализ алгоритмов в данном контексте связан, прежде всего, с оценкой временной сложности. Большинство алгоритмов имеют основной параметр , который в значительной степени влияет на время выполнения операций. Если же определяющих параметров несколько, то, как правило, один их них выражается как функция от остальных. Иногда используют и такой подход: рассматривают только один параметр , считая остальные константами.
Результатом анализа является асимптотическая оценка выполняемых алгоритмом операций в зависимости от длины входа, которая указывает порядок роста функции и результаты сравнения работы алгоритмов для больших данных. При этом оценка на реальных данных отличается от асимптотической тем, что она ориентирована на конкретные длины входов и число выполняемых алгоритмом операций.
Временная сложность алгоритма определяется асимптотической оценкой функции трудоемкости алгоритма для худшего случая, обозначается O(f(n)) и читается как «О большое» или «О-нотация». Асимптотический класс функций О включает в себя как средний, так и лучший случай, потому что запись O(f(n)) обозначает класс функций, скорость роста которых не более, чем f(n) с точностью до некоторой положительной константы . В зависимости от вида функции f(n) выделяют следующие классы сложности алгоритмов.
| 1 | Большинство инструкций большинства функций запускается один или несколько раз. Если все инструкции программы обладают таким свойством, то время выполнения программы постоянно. |
| log N | Когда время выполнения программы является логарифмическим, программа становится медленнее с ростом N . Такое время выполнения обычно присуще программам, которые сводят большую задачу к набору меньших подзадач, уменьшая на каждом шаге размер задачи на некоторый постоянный фактор. Будем рассматривать время выполнения, являющееся небольшой по величине константой. Изменение основания не сильно сказывается на изменении значения логарифма: при N=1 000, log N = 3 , если основание равно 10, или порядка 10, если основание равно 2; когда N=1 000 000 , значения log N увеличивается в два раза. При удвоении значения параметра log N растет на постоянную величину, а удваивается лишь тогда, когда N достигает N 2 . |
| N | Когда время выполнения программы является линейным, это обычно значит, что каждый входной элемент подвергается небольшой обработке. Когда N равно миллиону, таким же и является время выполнения. Когда N удваивается, то же происходит и со временем выполнения. Эта ситуация оптимальна для алгоритма, который должен обработать N вводов (или произвести N выводов). |
| N log N | Время выполнения, пропорциональное N log N , возникает тогда, когда алгоритм решает задачу, разбивая ее на меньшие подзадачи, решая их независимо и затем объединяя решения. Время выполнения такого алгоритма равно N log N . Когда N=1 000 000 ,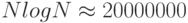 
. Когда N удваивается, тогда время выполнения более чем удваивается. |
| N 2 | Когда время выполнения алгоритма является квадратичным, он полезен для практического использования при решении относительно небольших задач. Квадратичное время выполнения обычно появляется в алгоритмах, которые обрабатывают все пары элементов данных (возможно, в цикле двойного уровня вложенности). Когда N=1 000 , время выполнения равно одному миллиону. Когда N удваивается, время выполнения увеличивается вчетверо. |
| N 3 | Похожий алгоритм, который обрабатывает тройки элементов данных (возможно, в цикле тройного уровня вложенности), имеет кубическое время выполнения и практически применим лишь для малых задач. Когда N=100 , время выполнения равно одному миллиону. Когда N удваивается, время выполнения увеличивается в восемь раз. |
| 2 N | Лишь несколько алгоритмов с экспоненциальным временем выполнения имеет практическое применение, хотя такие алгоритмы возникают естественным образом при попытках прямого решения задачи, например полного перебора. Когда N=20 , время выполнения имеет порядок одного миллиона. Когда N удваивается, время выполнения увеличивается экспоненциально. |
На основании математических методов исследования асимптотических функций трудоемкости на бесконечности выделены пять классов алгоритмов.
Класс 0 – это класс быстрых алгоритмов с постоянным временем выполнения, их функция трудоемкости O(1) . Промежуточное состояние занимают алгоритмы со сложностью O(log N) , которые также относят к данному классу.
Класс Р – это класс рациональных или полиномиальных алгоритмов, функция трудоемкости которых определяется полиномиально от входных параметров . Например, O(N), O(N 2 ), O(N 3 ) .
Класс L – это класс субэкспоненциальных алгоритмов со степенью трудоемкости O(N log N) .
Класс E – это класс собственно экспоненциальных алгоритмов со степенью трудоемкости O(2 N ) .
Класс F – это класс собственно надэкспоненциальных алгоритмов. Существуют алгоритмы с факториальной трудоемкостью, но они в основном не имеют практического применения.
Состояние памяти при выполнении алгоритма определяется значениями, требующими для размещения определенных участков. При этом в ходе решения задачи может быть задействовано дополнительное количество ячеек. Под объемом памяти, требуемым алгоритмом А для входа D , понимаем максимальное количество ячеек памяти, задействованных в ходе выполнения алгоритма. Емкостная сложность алгоритма определяется как асимптотическая оценка функции объема памяти алгоритма для худшего случая.
Таким образом, ресурсная сложность алгоритма в худшем, среднем и лучшем случаях определяется как упорядоченная пара классов функций временной и емкостной сложности , заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю.
Источник: intuit.ru