Датчик случайных чисел это программа

Генератор случайных чисел , как следует из названия, представляет собой процесс получения случайного числа каждый раз, когда это необходимо, без возможности установить шаблон из ранее сгенерированных чисел. Это число может быть сгенерировано либо алгоритмом, либо аппаратным устройством, и очень важно избежать любого предсказуемого результата.

Алгоритм генератора случайных чисел часто используется в видеоиграх, где он устанавливает разные результаты каждый раз, когда его запускают. Возможно, вы заметили, что даже если вы играете на одном уровне в игре, каждый раз, когда вы пытаетесь выполнить миссию, он не будет одинаковым. Различия не будут наблюдаться в локации или требованиях к миссии, но они будут наблюдаться в количестве приближающихся врагов и областях их появления, изменениях климата и различных препятствиях, которые встречаются между ними. Это делает игру более захватывающей и интересной.

Ломаем рандом генератор randstuff ru

В противном случае, после нескольких попыток игра покажется скучной, так как вы сможете предсказать события, которые произойдут дальше. Это может показаться простым, но для компьютера – генерировать случайные числа – это сложная задача, требующая следовать точным инструкциям, закодированным в нём.

Истинный ГСЧ против псевдо ГСЧ

Есть два типа генераторов случайных чисел: истинные и псевдо.

• Алгоритм истинного генератора случайных чисел создаётся с помощью аппаратного устройства, которое использует очень крошечные физические процессы для генерации случайных чисел. Так как алгоритм не написан; следовательно, истинный ГСЧ не может быть взломан для предсказания. Он обычно используется в системах, ориентированных на безопасность, по всему миру и в некоторых формах шифрования.
• Алгоритм генератора псевдослучайных чисел используется в областях, где нет проблем с безопасностью, а случайность используется, чтобы избежать повторений и сделать что-то более интересное для конечного пользователя. Реализовать технологию дешевле и быстрее, поскольку она не требует оборудования и может быть легко встроена в программный код. Хотя этот процесс не является полностью случайным и определяется на основе алгоритма, он больше подходит для игр и программ.

Какие приложения используют ГСЧ

Не во всех играх используется генератор случайных чисел, что делает их менее конкурентоспособными и часто утомительными, однако, новые игры почти всегда идут с генератором случайных чисел. Многие приложения и игры выигрывают от случайности, поскольку они могут приносить интерес и прибыль только в том случае, если они случайны:

• Азартные игры: бинго, карточные игры, лотереи и подобные игры.
• Игры со сбором добычи: все игры, требующие от игроков сбора добычи для использования в игровом процессе, например, PubG, Diablo и Borderlands используют ГСЧ. Возможность получать лучшую добычу каждый раз – вот причина, по которой люди становятся зависимыми от них.
• Приключенческие игры: такие игры, как Марио и Покемон Го используйте алгоритм генератора случайных чисел, чтобы определить, какие предметы будут добавлены, и каждый раз вы встречайтесь с новым претендентом на покемона.
• Процедурно-сгенерированные игры: все игры, в которых нет предварительно разработанных карт и уровней, но которые были разработаны в игре с использованием процедурного программирования, таких как Minecraft и Civilization. Это помогает создать всю игру с использованием алгоритма.
• Соревновательные игры: некоторые соревновательные игры, например, Counter-Strike используйте алгоритм генератора случайных чисел, чтобы регулировать, как пули поражают цели.

Помимо игровых приложений, есть код случайных чисел в JavaScript, используемый разработчиками и кодировщиками во всём мире для включения генератора случайных чисел в их программы. У Google есть свой очень интересный инструмент, который также основан на теории случайных чисел JavaScript и может генерировать случайные числа. Этот инструмент может пригодиться, когда вы играете в игры с друзьями и семьей. Чтобы посмотреть ГСЧ Google, нажмите здесь.

Генератор случайных чисел на Python

Манипуляции с ГСЧ

Я уже обсуждал различия между истинным ГСЧ и псевдо ГСЧ и тот факт, что в играх используется псевдо ГСЧ, основанный на алгоритме. Некоторые увлеченные геймеры используют утилиты эмуляции для анализа игр и выявления лазеек, которые можно использовать для управления результатами, даже если используется алгоритм генератора случайных чисел.

ГСЧ на основе алгоритма использует начальное число, которое представляет собой комбинацию определенных факторов и генерирует результат в игре. Это применяемые законы математики, и поскольку 1+1 всегда равно 2, аналогично, если известны факторы в игре, которые приносят желаемый результат, то вы всегда можете достичь того же результата.

Например, если игра требует от игрока выбрать определенного персонажа с определенными усилениями, и результатом будет легкая битва с боссом, то этот шаблон будет постоянным, и все, кто выберет одни и те же варианты, будут иметь одинаковые результаты. Но, для обычного игрока это было бы невозможно, и псевдо-ГСЧ всегда казался бы истинным ГСЧ.

Почему геймеры ненавидят ГСЧ

Геймеров можно разделить на соревнующихся игроков, спидраннеров и средних игроков. Любой конкурентоспособный игрок, овладевший техникой игры и движениями, захочет бросить вызов другим игрокам и побеждать на основе навыков и, несомненно, возненавидит игру, если на результат повлияет генератор случайных чисел. Точно так же спидраннер хотел бы завершить игру как можно скорее, но алгоритм генератора случайных чисел включает тормоза, создавая каждый раз неизвестные и неожиданные сценарии в игре.

В идеале геймеры хотели бы уменьшить количество случаев, когда они сталкиваются со средством генерации случайных чисел в игре, чтобы держать весь игровой процесс и результат под своим контролем. Но, это возможно лишь до определенной степени. И когда геймер часами осваивает игрового персонажа и его движения, он больше всего расстраивается, когда случается что-то случайное, и вся стратегия нарушается. Иногда это тоже действует как благословение, но обычно это проклятие.

Кто такой RNGesus?

Обычные игроки, которые играют только для того, чтобы развлечься или скоротать время, не заботятся о результате игры. Но, опытные профессиональные игроки ненавидят проигрывать только потому, что удача была не в их пользу.

Игроки, которые проигрывают, часто винят в своих поражениях злой ГСЧ, который выгоден их противникам. Там где зло, должен быть Бог – RNGesus.

Среди геймеров во всем мире появился новый термин, RNGesus, который больше соответствует игре слов с «Иисусом». Поскольку Иисус Христос считается нашим спасителем в реальном мире, RNGesus – это вообразимая сущность, созданная для спасения игроков от пагубных последствий ГСЧ. Это нигде не доказывается, но началось как миф, а теперь распространилось по игровому сообществу, как лесной пожар.

Окончательный вердикт по ГСЧ – хорошо или плохо?

На этот вопрос сложно ответить, и определенно не может быть одного и того же ответа для всех. В то время как среднестатистические геймеры утверждают, что это хорошо, другим нравится соревновательный дух.

Алгоритм генератора случайных чисел действительно сохраняет непредсказуемость и интересность каждый раз, когда вы играете на одном уровне. Он стал важной частью многих игр, предлагая разнообразие, например, головоломки, карточные игры, ролевые игры и многие другие. Но, для геймеров, которые верят в навыки как в единственный способ пройти игру, ГСЧ подрывает их потенциал, когда вытаскивает что-то случайное из коробки.

Игры предназначены для развлечения и удовольствия. Если у вас хороший ГСЧ, вы сможете получить лучшие варианты, несмотря на низкие шансы. В случае плохого ГСЧ, вы получите худший результат, даже если вы играли в игру именно так, как должно. Правда в том, что это не то, что можно воспринимать так серьёзно, особенно если оно основано на алгоритме генератора случайных чисел.

Источник: webznam.ru

Генераторы случайных чисел в разных ОС

Как-то поздним летним вечером мне пришлось разобраться, как устроены генераторы случайных чисел в Windows и Linux. Собственно, в этой статье я попробую привести саккумулированную информацию, и преподнести ее максимально простыми словами, без необходимости лезть в исходники, туториалы и статьи.

Генераторы псевдослучайных чисел

С развитием технологий и безопасности мы все больше и больше нуждаемся в действительно случайных числах, которые нельзя было бы предсказать извне. Почему? В первую очередь из-за шифрования, ведь с каждым годом растет количество пересылаемого трафика, и при этом хочется иметь достаточную степень безопасности наших данных. И вот в тот момент, когда нужно сгенерировать случайное число, у наших компьютеров возникают проблемы, поскольку они созданы быть максимально послушными, предсказуемыми и детерминированными для того, чтобы все результаты при одинаковых входных данных воспроизводились, иначе бы весь мир развалился.

Выход из данной ситуации нашелся и достаточно изящный — а давайте возьмем «предсказуемый» генератор псевдослучайных чисел (ГПСЧ) и будем его инициализировать случайными битами(пока не задумываемся откуда и как взятыми). Из небольшого числа действительно случайных событий мы сможем получить достаточно хорошие случайные числа в большом количестве. И пока «злоумышленник» не имеет доступа к внутреннему состоянию нашего компьютера, можно полагаться на сгенерированные последовательности таких чисел. Или же можно контролировать количество выданных бит и не позволять отдавать больше энтропии, чем есть в инициализирующем состоянии, тогда предсказать следующий бит будет невозможно.

Немного про энтропию

Чтобы не перегружать текст, я решил не давать таких определений как информационная энтропия и количество информации. Многим они и так знакомы. Поэтому спокойно позволяю себе использовать такие фразы, как «больше энтропии», «пул энтропии», «источник энтропии». А для тех, кто столкнулся с этими терминами впервые, — wiki или воспринимать энтропию интуитивно, как меру случайности(или саму случайность, например «источник энтропии»), и чем она больше, тем «более случайны» полученные биты.

Генератор псевдослучайных чисел — это функция, которая перемешивает входные биты, применяя к ним простые операции несколько раз, выдает наружу результат, который и является последовательностью случайных бит. Для примера рассмотрим алгоритм ChaCha20, применяемый в Linux, и SP800-90 AES-CTR-DRBG в Windows

• ChaCha20 — это развитие алгоритма Salsa20. Он основан на комбинации операций: 32-битное сложение, XOR и побитовое вращение. Если кратко: матрица 4 * 4 заполняется особой константой, ключом, счетчиком и одноразовым числом для текущей итерации, а затем происходит перемешивание бит в течение 20 раундов алгоритма. При этом нечетные раунды отвечают за изменения бит по столбцам матрицы, а четные за изменения по диагоналям. Полученные на выходе биты и есть псевдослучайное число, которое к тому же является входным состоянием для следующего запуска генератора. Но, так как при таком подходе было бы очень легко предсказать все следующие числа, существует обязательная операция изменения ключа после каждого запроса;

// linux/lib/crypto/chacha.c for (i = 0; i < nrounds; i += 2) < // Odd round x[0] += x[4]; x[12] = rol32(x[12] ^ x[0], 16); x[1] += x[5]; x[13] = rol32(x[13] ^ x[1], 16); x[2] += x[6]; x[14] = rol32(x[14] ^ x[2], 16); x[3] += x[7]; x[15] = rol32(x[15] ^ x[3], 16); x[8] += x[12]; x[4] = rol32(x[4] ^ x[8], 12); x[9] += x[13]; x[5] = rol32(x[5] ^ x[9], 12); x[10] += x[14]; x[6] = rol32(x[6] ^ x[10], 12); x[11] += x[15]; x[7] = rol32(x[7] ^ x[11], 12); x[0] += x[4]; x[12] = rol32(x[12] ^ x[0], 8); x[1] += x[5]; x[13] = rol32(x[13] ^ x[1], 8); x[2] += x[6]; x[14] = rol32(x[14] ^ x[2], 8); x[3] += x[7]; x[15] = rol32(x[15] ^ x[3], 8); x[8] += x[12]; x[4] = rol32(x[4] ^ x[8], 7); x[9] += x[13]; x[5] = rol32(x[5] ^ x[9], 7); x[10] += x[14]; x[6] = rol32(x[6] ^ x[10], 7); x[11] += x[15]; x[7] = rol32(x[7] ^ x[11], 7); // Even round x[0] += x[5]; x[15] = rol32(x[15] ^ x[0], 16); x[1] += x[6]; x[12] = rol32(x[12] ^ x[1], 16); x[2] += x[7]; x[13] = rol32(x[13] ^ x[2], 16); x[3] += x[4]; x[14] = rol32(x[14] ^ x[3], 16); x[10] += x[15]; x[5] = rol32(x[5] ^ x[10], 12); x[11] += x[12]; x[6] = rol32(x[6] ^ x[11], 12); x[8] += x[13]; x[7] = rol32(x[7] ^ x[8], 12); x[9] += x[14]; x[4] = rol32(x[4] ^ x[9], 12); x[0] += x[5]; x[15] = rol32(x[15] ^ x[0], 8); x[1] += x[6]; x[12] = rol32(x[12] ^ x[1], 8); x[2] += x[7]; x[13] = rol32(x[13] ^ x[2], 8); x[3] += x[4]; x[14] = rol32(x[14] ^ x[3], 8); x[10] += x[15]; x[5] = rol32(x[5] ^ x[10], 7); x[11] += x[12]; x[6] = rol32(x[6] ^ x[11], 7); x[8] += x[13]; x[7] = rol32(x[7] ^ x[8], 7); x[9] += x[14]; x[4] = rol32(x[4] ^ x[9], 7); >

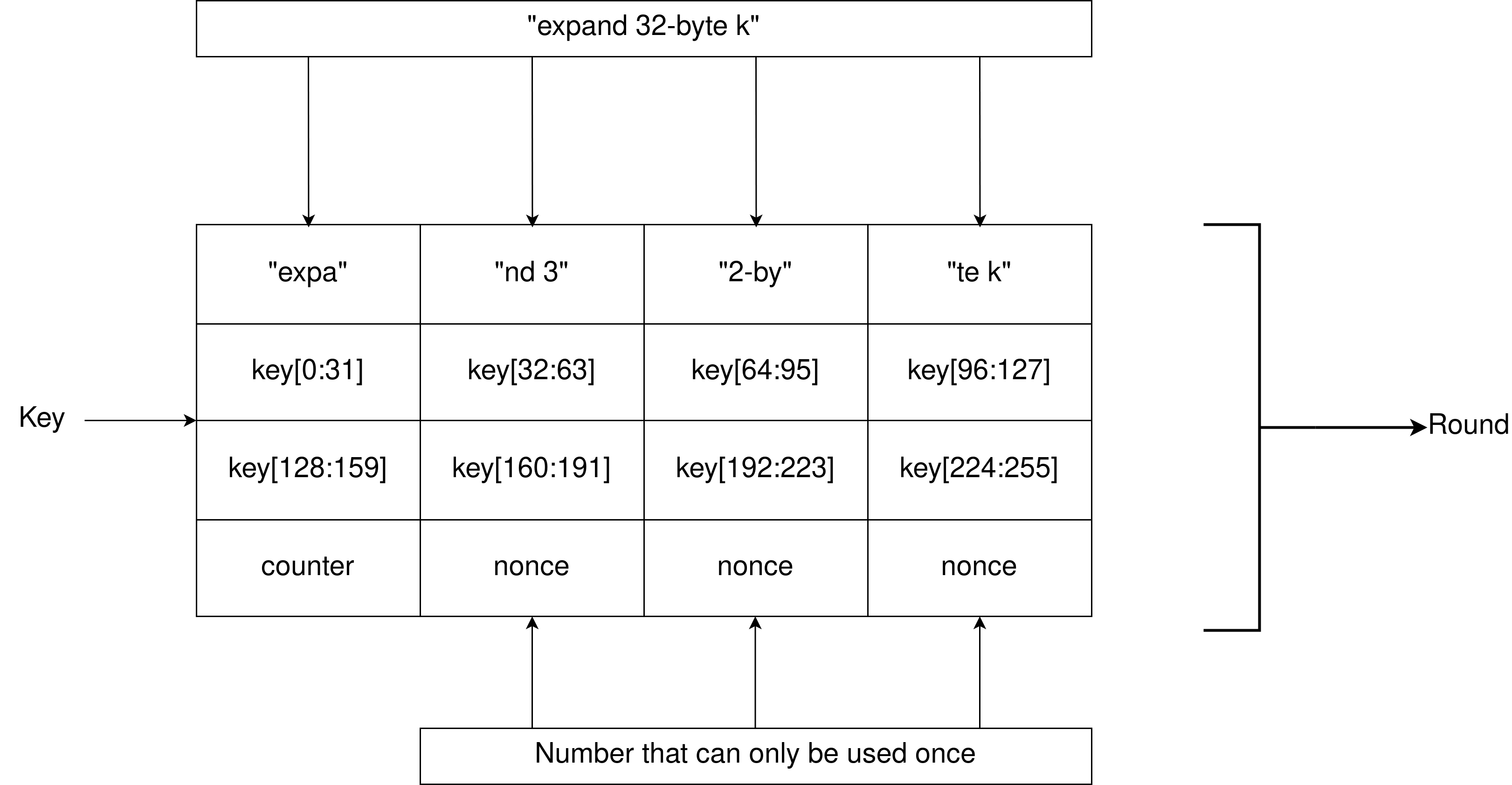
• SP800-90 AES CTR DRBG (англ.: CounTeR mode Deterministic Random Byte Generator) — это криптографически стойкий генератор псевдослучайных чисел, основанный на блочном шифровании AES (англ.: Advanced Encryption Standard) в режиме счетчика. Текущее состояние генератора описывается тремя объектами: ключ K, вектор V, который является счетчиком, и счетчик повторного заполнения counter. В упрощенном виде процесс создания выходной последовательности можно разбить на 2 части:

• Создание ключа K и начального вектора V при помощи алгоритма обновления и дополнительных входных данных;
• Создание необходимых псевдослучайных чисел, происходит шифрованием счетчика, при этом счетчик инкрементируется после каждого шага. Само шифрование происходит при помощи алгоритма AES с сгенерированным ключом. Таким образом этот алгоритм лишен необходимости дополнительного перемешивания начального состояния после каждого обращения, как это было в ChaCha.

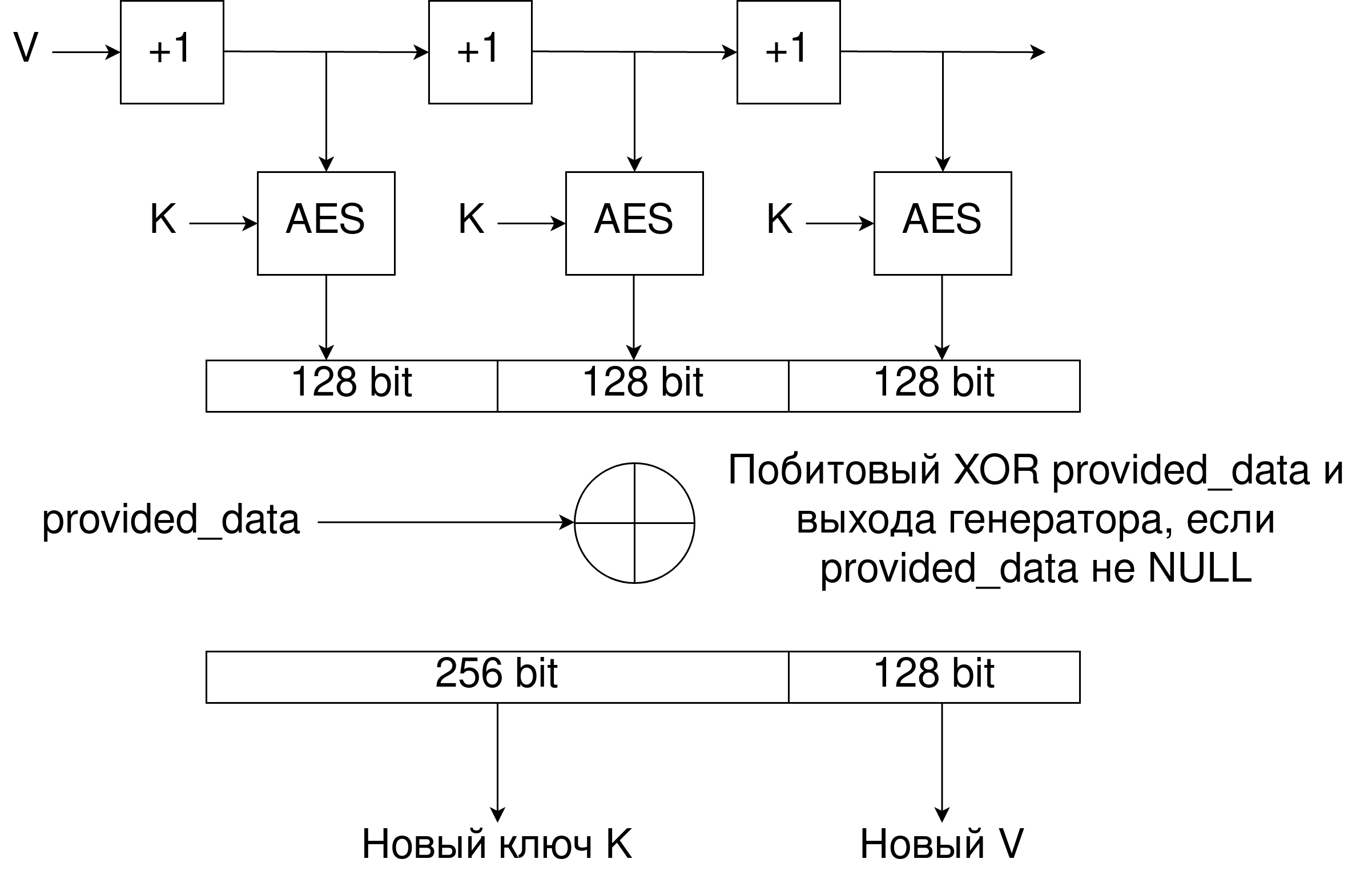
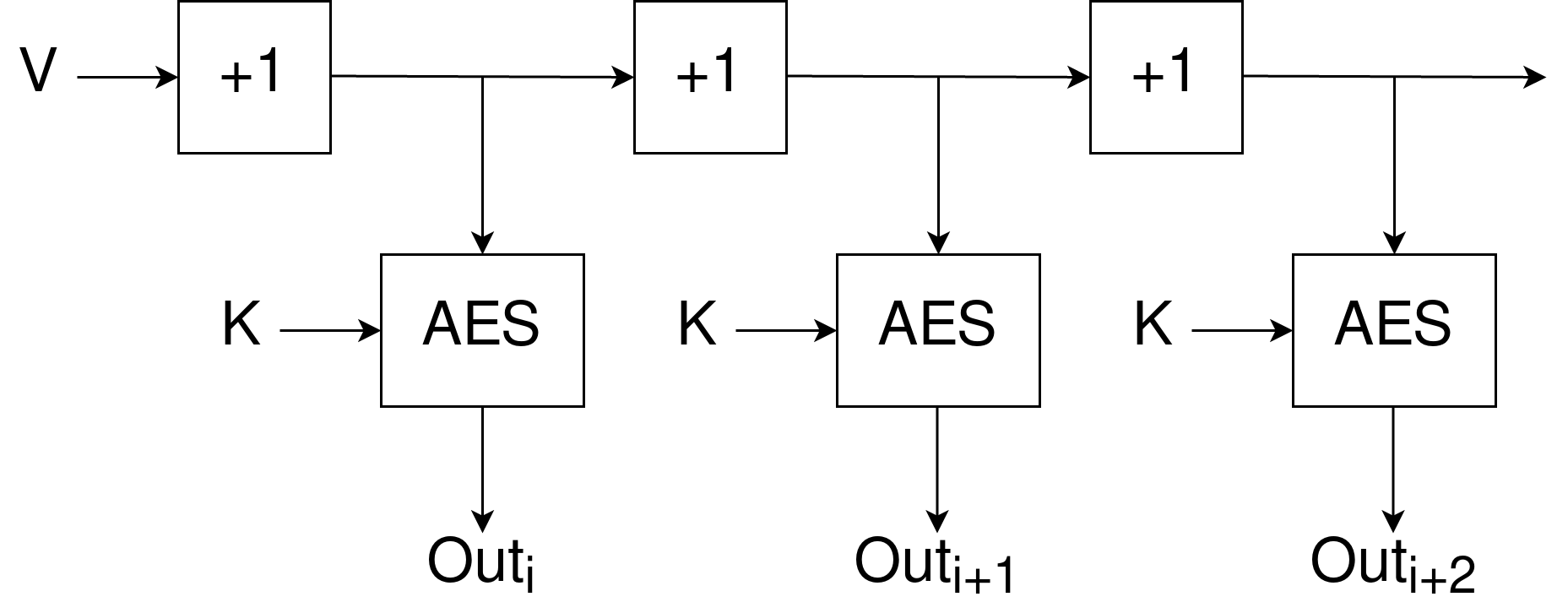
Случайные события

Осталось разобраться с самым интересным — чем инициализировать ГПСЧ, чтобы получать действительно случайные числа? Кроме того, проблема состоит не только в инициализации, но и в постоянной переинициализации, которая необходима для предотвращения возможности предсказания следующего состояния. Вот тут и начинается самая интересная и важная работа по поиску случайности в событиях в системе.

Linux

Основные правила выбора событий, которые расцениваются как случайные. Во-первых, эти события должны быть недетерминированные. Во-вторых, их должно быть тяжело пронаблюдать извне. Эти случайные события добавляются в пул энтропии (просто массив чисел), перемешиваясь с его содержимым с помощью специальной CRC-подобной хэш-функции.

Она выполняется быстро, чтобы ее можно было применять после каждого интересующего события в системе, и достаточно хороша, если предполагать, что случайные события заполняют пул не вредоносным образом. При этом при добавлении события в пул, происходит учет прибывшего количества энтропии.

В данный момент используется 4 типа источников случайных событий:

• Информация от устройств, которая должна быть разной на физически разных машинах, например MAC адрес сетевой карты. Фактически, это не добавляет энтропии системе, но позволяет в очень плохих случаях (запуск с одного образа) на разных устройствах получать разные состояния;
• Информация от таймера, прерывания, типа прерывания, значения;
• Время прерывания;
• Информация о времени поиска блока на диске. Однако на современных SSD это достаточно плохой источник случайности, так как у них время поиска сравнительно маленькое и примерно одинаковое всегда.

Чтобы инициализировать или переинициализировать ГПСЧ, необходимо из пула энтропии достать несколько случайных байт. Для этого, весь пул хэшируется алгоритмом SHA-1, а хэш-сумма выдается как случайный набор бит. При этом предпринимаются меры для обеспечения безопасности генератора в будущем. Во-первых, результат хэширования перемешивается с пулом, чтобы по выходному значению нельзя было восстановить текущее состояние. Во-вторых, происходит постоянная оценка оставшегося количества энтропии в пуле.

Из-за последнего существует 2 способа взаимодействия со случайными числами в Linux — /dev/random и /dev/urandom. Первый блокируется, когда оценка по количеству энтропии становится ниже нуля, а второй выдает числа всегда, даже если пул не пополняется случайными битами. При этом числа все еще могут оставаться достаточно случайными для требуемой задачи.

Стоит добавить, что на многих шагах, где это имеет смысл, в коде добавлены обращения к «железным» генераторам случайных чисел, которые работают быстрее и дают более качественную энтропию. Это, возможно, было бы не так важно, но Intel еще в Ivy Bridge добавили инструкции RDRAND и RDSEED, позже и AMD сделали это. Таким образом у многих современных компьютеров в CPU есть быстрый генератор случайных чисел. Почему это необходимо — будет объяснено в заключении.

Windows

В Windows процесс создания случайных чисел подчинен достаточно сложной древовидной структуре. Есть три типа источников энтропии, которые отличаются предназначением и качеством. Энтропия, получаемая из них, используется для инициализации и переинициализации корневого ГПСЧ — все случайные числа тем или иным образом получаются из него.

Так как в современных многоядерных компьютерах было бы непозволительно медленно иметь только один генератор, то для каждого логического CPU, создается свой ГПСЧ, который инициализируется корневым. Далее, на каждый пользовательский процесс, заводятся и инициализируются свой ГПСЧ и его дочерние генераторы для каждого логического CPU. Таким образом мы получаем что-то вроде дерева генераторов.

Все генераторы, кроме корневого, переинициализируются, когда понимают, что их состояние устарело. Это происходит с помощью ведения и сравнения эпох. Счетчик инкрементируется каждый раз, когда корневой генератор переинициализируется. При этом каждый из его «потомков» в дереве локально запоминает состояние счетчика при его собственной переиницализации.

Корневой генератор заполняется по расписанию — при загрузке системы, а далее с экспоненциально растущим периодом: 1, 3, 9, 27 секунд и т.д. Максимальное значение периода составляет 1 час.

В качестве источников энтропии в Windows используются:

• Время прерываний (основной источник) — при каждом прерывании берется отметка о времени с помощью чтения с TSC (англ.: TimeStamp Counter) и записывается в специальный массив на 256 байт компактным образом;
• TPM (англ.: Trusted Platform Module) — выдает 40 байт на старте и 64 байта при каждой переинициализации, но из-за ограничений, не может этого делать чаще, чем раз в 40 минут;
• RDRAND/RDSEED — «железные» генераторы, предоставляемые процессором;
• Seed файл — запись в реестре, которая создается ОС во время работы и используется во время следующей загрузки;
• Внешняя энтропия — запись в реестре, которая делается установщиком для первого запуска системы, но также может быть использована пользователем в будущем, чтобы влиять на процесс инициализации;
• ACPI-OEM0 — создается гипервизором Hyper-V и заполняет при каждом запуске гостевой ОС;
• Данные из драйверов — хэшируются и представляются как очень плохой источник энтропии, который, однако, позволяет по-разному инициализировать систему на разных физически машинах;
• UEFI — случайные числа из UEFI-драйвера;
• Отметка о времени старта системы — не очень хороший источник, но снижающий вероятность того, что, стартуя с одного образа системы, машины получат одинаковые состояния;
• Уникальное (не случайное) число от Hyper-V — помогает бороться с повторением состояния при запуске снапшота системы.

Как правило, не только Hyper-V при работе с Windows предоставляет такие улучшения. Многие гипервизоры «прикидываются» Hyper-V, чтобы обеспечивать такой же функционал и использовать встроенные возможности по повышению производительности при работе с Windows.

Во время старта системы данные с 7 источников (Seed файл, внешняя энтропия, TPM, RDRAND, ACPI-OEM0, UEFI и время старта) хэшируются SHA-512 и используются для инициализации SP800-90 AES-CTR-DRBG. Уже во время работы системы, данные предоставленные источником, помещаются в пул (за исключением первого раза, когда они идут сразу на переинициализацию корневого ГПСЧ).

Заключение

Как можно было заметить, многие источники случайных событий связаны с текущим состоянием машины, следовательно при виртуализации могут начаться проблемы. В Linux в комментариях к коду иногда открыто признается эта проблема. В Windows с Hyper-V (или другим гипервизором, «прикидывающимся» им) пытаются с этим бороться, но сама проблема все же иногда проявляется. Ситуация несколько облегчается, тем фактом, что в современных процессорах есть «железные» генераторы случайных чисел, а так же существуют виртуализированные генераторы, которые подсовывают случайные числа хостовой ОС гостевой. Ведь нельзя оставлять это на волю случая.

Источник: habr.com

Уроки 52 — 54
Понятие случайного числа
Датчик случайных чисел в Паскале
Поиск чисел в массиве
(§ 19. Одна задача обработки массива)
Разработка программы поиска числа в случайно сформированном массиве

Сначала несколько слов о случайных числах. Все себе представляют игральный кубик, имеющий шесть граней. При каждом бросании кубика выпадение какого-то числа есть случайное событие. С равной вероятностью может выпасть любое число от 1 до 6. Результат бросания кубика — это случайное число. А теперь представьте себе кубик с 10 гранями.

Правда, кубиком его можно назвать только условно. Это десятигранник, на гранях которого нанесены числа от 1 до 10. Результат бросания такого «кубика» — случайное число в диапазоне от 1 до 10. Еще один пример. При розыгрыше лотереи из вращающегося барабана достают пронумерованные шары.

Выпавший номер шара — случайное число.

Датчик случайных чисел на Паскале

В языках программирования, как правило, имеется аналог подобного «кубика» или лототрона, позволяющий получать случайные числа. Он называется датчиком случайных чисел. Это стандартная функция. В Паскале она записывается так: random (X) . Здесь X — целое число. При выполнении функции ее результатом становится целое число в диапазоне от 0 до X. Например, если X = 50, то в результате можем получить любое целое число от 0 до 50.

Приведем программу, которая демонстрирует работу датчика случайных чисел на Паскале:

По этой программе на экран выводится десять случайных чисел из диапазона от 0 до 50. Вот результат тестового выполнения этой программы:

0 3 17 20 27 7 31 16 37 42

А теперь вернемся к условию задачи. Получающиеся с помощью датчика случайные числа «раскладываются» по элементам массива. Назовем массив Rand, а число элементов в нем пусть будет равно 20. Число, которое нужно искать в массиве, будет вводиться в переменную X.

Алгоритм поиска числа в массиве

На рисунке 2.11 приведена блок-схема алгоритма поиска в массиве Rand величины X с подсчетом числа ее вхождений в массив в переменной NumberX.

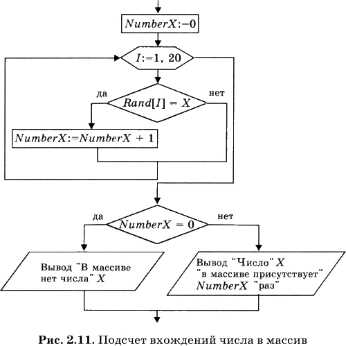
Обратите внимание на блок, отображающий цикл с параметром. Он имеет форму вытянутого шестиугольника. В блоке записывается параметр цикла (переменная I), начальное и конечное значения параметра через запятую (:=1, 20).

Переменная NumberX играет роль счетчика. Вначале ей присваивается ноль. Затем в цикле происходит перебор всех элементов массива, и при каждом выполнении условия равенства к счетчику добавляется единица. Так всегда организуются счетчики в программах! В результате выполнения программы на экран будет выведен один из двух вариантов ответа: либо сообщение, что в массиве нет данного числа, либо сообщение о том, сколько раз это число присутствует в массиве, если оно там обнаружено.

Следующая страница § 19. Одна задача обработки массива. Программа поиска числа в массиве

Источник: xn—-7sbbfb7a7aej.xn--p1ai