Crc что за программа

Содержание

Автор должен чистосердечно раскаяться в том, что идея данного способа использования CRC для защиты исполняемых файлов от искажения целиком и полностью украдена им из книги Лу Гринзоу «Философия программирования Windows 95/NT» (Символ, Санкт-Петербург,1997), однако просит принять во внимание следующие, смягчающие его вину обстоятельства:

В книге исходники приведены не полностью, не хватает одного заголовочного файла.
Используется CRC16
Собственно реализация, безусловно, рабочая, но, IMHO, уж больно “мутная”.

Что еще мог сделать в этой ситуации русский программист? Конечно, только одно – “переписать это все нафиг” :).

Идея

Для тех, кто не читал Лу Гринзоу (фи:( ) приведу идею метода. Для того, чтобы при подсчёте CRC учитывались только данные исполняемого файла и не учитывалась сама CRC, добавим в исходные тексты программы следующую глобальную структуру данных CRC_DATA:

struct CRC_DATA < BYTE label[ 16 ]; // метка (маячок) для поиска места CRC в файле DWORD crc; // собственно посчитанная CRC файла > CrcData = «0123456789ABCDE»>, 0>; //

Придуманная нами уникальная (в пределах файла) метка label поможет найти в исполняемом файле нашей программы место (DWORD crc), где находится рассчитанная CRC, и которое поэтому не должно учитываться при подсчёте.

57. CRC алгоритм (Урок 48. Теория)

ПРИМЕЧАНИЕ

В рассматриваемой далее реализации не имеет значения кратность длины метки установленному в свойствах проекта выравниванию – Struct Member Aligment, т.к. переменная CrcData.crc, как таковая, нигде в программе не используется. Она нужна только как гарантия наличия 4-х неиспользуемых байт после метки. Именно эти 4 байта будут использоваться для записи и чтения CRC. В зависимости от длины метки и используемого выравнивания они могут совпадать, а могут и не совпадать с 4-мя байтами переменной CrcData.crc.

Что дает и чего не дает данный способ

Начну с конца – использование CRC затрудняет, но не исключает полностью возможность искажения файла злоумышленником (см. например [1]), так что о 100%-й надежности определения факта искажения речь не идет. Утешимся, однако, тем, что под нашим контролем останутся искажения при передаче по каналам связи, записи/перезаписи, изменения, внесённые вирусами, а также малолетними «хацкерами» с редакторами ресурсов в руках.

Другие способы самоконтроля целостности исполняемого файла

Использование стандартного поля PE-заголовка и функции MapFileAndCheckSum

Установив в свойствах проекта опцию Set CheckSum (ключ /RELEASE) мы заставим линкер после каждой перекомпиляции рассчитывать контрольную сумму для файла и записывать ее в соответствующее поле PE-заголовка. Следующий код демонстрирует способ проверки контрольной суммы при запуске exe-файла:

Достоинства : Все очень просто
Недостатки : Если известно, что файл защищен данным способом пересчитать для измененного файла контрольную сумму очень просто – место хранения и функция расчета контрольной суммы — стандартные.

Использование криптографии – цифровая подпись

Достоинства : Правильная реализация обеспечивает высокую криптографическую стойкость, подделка подписи, в отличии от CRC практически не возможна.
Недостатки : Проблема однако в том, что в рассматриваемом случае само проверки исполняемого файла весь код проверки подписи будет находится в том же самом исполняемом файле, и доступен для взлома точно также как и механизм проверки CRC, а значит нет практически никакого реального увеличения надежности проверки.

Реализация

В демонстрационном проекте (VC7) приведены исходные тексты класса CSelfSafe , делающего для нас необходимую минимальную работу по контролю целостности файла и расчету CRC:

Ошибки CRC

#pragma once #include #include «filemap.h» using namespace std; class CSelfSafe < public: // файл будет потом CSelfSafe(); // работать с файлом, переданным через HMODULE CSelfSafe( HMODULE hmod ); // работать с файлом с заданным именем CSelfSafe( string fname ); // новое имя файла для работы void NewFile( string fname ); void NewFile( HMODULE hmod ); ~CSelfSafe( void ); // получить строку с сообщением об ощибке string GetErrStrAnsi() const; // тоже для консольных приложений string GetErrStrOem() const; // подсчитать и сверить CRC для заданного файла BOOL CheckCRC(); // подсчитать и записать CRC в заданного файла BOOL WriteCRC(); protected: // имя проверяемого файла string filename; // сообщение об ошибке stringstream errstrm; // обработываемый файл, отображенный в память CFileMap targetfile; // найти место для CRC в файле BOOL OpenFileAndFindCRCpos( BYTE ** crcpos, BOOL toWrite = FALSE ); // посчитать CRC файла исключая собственно значение CRC в позиции crcpos DWORD SynCRC( BYTE * crcpos ); >;

Оставим пока в стороне конструкторы и способы задания имени контролируемого файла, начнем с основных моментов.

Поиск места для записи/ чтения CRC кода

Используем отображения контролируемого файла в память, чтобы иметь возможность работать с ним, как с обычной последовательностью байтов.
Применим алгоритм стандартной библиотеки C++ search , чтобы найти в нем нашу метку, обозначающую место хранения CRC.
Проверим, что после этой метки еще осталось место для записи 4-х байт CRC кода.
Повторим поиск от конца метки до конца файла, чтобы убедиться в том, что в файле случайно не образовалось еще одной такой же последовательности байт, т.к. в этом случае нам не удастся определить правильное место для хранения CRC кода.

Ситуация с двумя метками регулярно возникает для Debug-версий исполняемых файлов. Помогает полная перекомпиляция.

Ниже приведена реализация метода поиска места для CRC — OpenFileAndFindCRCpos():

// открыть файл и найти место для CRC BOOL CSelfSafe::OpenFileAndFindCRCpos( BYTE ** crcpos, BOOL toWrite ) < // открываем файл, отображаем в память if ( !targetfile.Open( filename.c_str(), toWrite ) ) < errstrm.clear(); errstrm.str( «» ); errstrm «Невозможно открыть файл ‘» << filename «‘»; return FALSE; > // указатель на конец файла, будет нужен несколько раз BYTE* file_end = targetfile.Base() + targetfile.Size(); // ищем метку, после которой идет место для CRC BYTE* label_start = search( targetfile.Base(), file_end, CrcData.label, CrcData.label + sizeof( CrcData.label ) ); if ( label_start == file_end ) < errstrm.clear(); errstrm.str( «» ); errstrm «В файле ‘» << filename «‘ не найдено место хранения CRC»; return FALSE; > // CRC — сразу после метки и смещения *crcpos = label_start + sizeof( CrcData.label ); if ( ( *crcpos + sizeof( DWORD ) ) > file_end ) < // при попытке записи/чтения в это место, вылетим // за конец файла errstrm.clear(); errstrm.str( «» ); errstrm «Недопустимое место для хранения CRC в файле ‘» << filename «‘»; return FALSE; > // метка найдена, на всякий случай ищем вторую, // начиная сразу после первой найденной метки if ( search( label_start + sizeof( CrcData.label ), file_end, CrcData.label, CrcData.label + sizeof( CrcData.label ) ) != file_end ) < // нашли две метки, это уже безобразие, метка в файле // должна быть одна, иначе непонятно, куда писать CRC errstrm.clear(); errstrm.str( «» ); errstrm «В файле ‘» << filename «‘ найдено 2 места для хранения CRC, должно быть только одно»; return FALSE; > return TRUE; >

Подсчет CRC и запись подсчитанной суммы в файл

После получения от OpenFileAndFindCRCpos() указателя на место для хранения CRC в файле нам остается только подсчитать CRC32, исключив из подсчета те самые четыре байта, в которых будет храниться CRC, и записать на это место подсчитанную сумму:

Контроль CRC

Ищем место, где хранится CRC, считываем контрольную сумму, сохраненную в файле, и сравниваем с рассчитанной:

// подсчитать и сверить CRC для заданного файла BOOL CSelfSafe::CheckCRC() < // указатель на CRC, сохраненную в файле BYTE * crcpos = NULL; // результат сверки CRC BOOL ret = FALSE; // ищем место, где в файле записана CRC if ( OpenFileAndFindCRCpos( // нашли, сравниваем то, что записано в файле, // с CRC, подсчитанной только что if ( *reinterpret_cast(crcpos) == SynCRC( crcpos ) ) ret = TRUE; else < // устанавливаем ошибку errstrm.clear(); errstrm.str( «» ); errstrm «Файл ‘» << filename «‘: неверное значение CRC»; ret = FALSE; > > else < // расшифровка ошибки дана в OpenFileAndFindCRCpos ret = FALSE; > // закрываем файл targetfile.Close(); return ret; >

Порядок применения CSelfSafe

Пример использования метода дан в демонстрационном проекте.

Создайте объект класса CSelfSafe , передав ему в конструкторе или в методе NewFile() HMODULE или строку с именем контролируемого файла. В процедуре запуска exe или dll, а также, в порядке паранойи, по некоторым событиям в вашей программе вызывайте метод CheckCRC() для контроля целостности.

Естественно, после каждой перекомпиляции программы на нее надо натравливать утилитку, которая, используя тот же самый CSelfSafe , будет с помощью метода WriteCRC() подсчитывать CRC и записывать ее в нужное место. Это, пожалуй, единственное неудобство при использовании данного метода, но с другой стороны, зачем еще нужен Post Build Step? 🙂

Не забудьте поменять для себя последовательность байтов в метке на нечто более редко встречающееся для затруднения обнаружения ее в исполняемом файле, с одной стороны, и для исключения ложных срабатываний при поиске, с другой стороны.

Тестовая программа из демонстрационного проекта при запуске с параметром (именем исполняемого файла) рассчитывает для него (файла) контрольную сумму и записывает в предназназначенное для этого место, а при запуске без параметра производит самопроверку CRC:

int _tmain( int argc, _TCHAR* argv[] ) < // инициализация CRTDBG для контроля утечек памяти // см. также // #define _CRTDBG_MAP_ALLOC // #include // в stdafx.h _CrtSetDbgFlag( _CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF ); CSelfSafe selfs; if ( argc == 1 ) < // argv[0] в данном случае использовать нельзя, если // программу вызовут без полного пути к selfsecureexe, // и она запустится из одного из каталогов, доступных по // PATH, не найдем «сами себя» для самопроверки. char myname[_MAX_PATH]; ::GetModuleFileName( NULL, myname, sizeof(myname) ); selfs.NewFile( myname ); if ( !selfs.CheckCRC() ) < cout return 0; > else < cout «CRC in file » << myname » is cheked out!» > else < selfs.NewFile( argv[1] ); cout «Writing CRC into file » << argv[1] «. » if ( !selfs.WriteCRC() ) < cout return 0; > else < cout «CRC is written into file » << argv[1] » !» cout «Checking CRC of » << argv[1] «file. » if ( !selfs.CheckCRC() ) < cout return 0; > else < cout «CRC in file » << argv[1] » is cheсked out!» > _getch(); return 0; >

Дополнительная информация по CRC

Anarchriz/DREAD. “CRC, и как его восстановить”
Ross N. Williams. “Элементарное руководство по CRC алгоритмам обнаружения ошибок”

Эта статья опубликована в журнале RSDN Magazine #3-2003. Информацию о журнале можно найти здесь

Источник: www.rsdn.org

Русские Блоги

Начало работы с алгоритмом CRC (Cyclic Redundancy Check)

Введение в алгоритм циклического избыточного кода (CRC) для встроенных программистов

предисловие

Проверка CRC (циклическая проверка избыточности) является наиболее часто используемым методом проверки при передаче данных. При разработке встроенного программного обеспечения алгоритм CRC часто используется для проверки различных данных. Поэтому освоение базового алгоритма CRC должно быть базовым навыком для программистов встраиваемых систем. Тем не менее, немногие из знакомых мне встраиваемых программистов действительно могут освоить алгоритм CRC, и большинство кодов CRC, которые я обычно вижу в проектах, являются очень неэффективными методами реализации.

На самом деле, в Интернете есть очень хорошая статья, которая представляет алгоритм CRC. Автор — Росс Уильямс. Название — «БЕЗБОРОЧНОЕ РУКОВОДСТВО ПО АЛГОРИТМАМ ОБНАРУЖЕНИЯ ОШИБОК CRC». Я часто рекомендую эту статью друзьям, которые спрашивают меня об алгоритме CRC, но многие друзья жалуются мне, что оригинальный текст слишком длинный и написан на английском языке.

Надеюсь, я смогу написать более короткую статью, так что эта статья здесь. Однако мой уровень не лучше, чем у Росса Уильямса, и моя статья определенно не так хороша, как у Росса Уильямса. Поэтому друзья, которые не испытывают затруднений при чтении по-английски, должны прочитать оригинальный текст Росса Уильямса.

Читатели этой статьи ориентированы на разработчиков программного обеспечения, особенно программистов, занимающихся разработкой встроенного программного обеспечения, а не на ученых, специализирующихся на математике или коммуникациях (я не настолько продвинут, как этот уровень). Таким образом, цель этой статьи — представить основной принцип и реализацию алгоритма CRC. Используемая математика должна контролироваться до глубины, понятной для учащихся старших классов.

Кроме того, учитывая, что большинство встроенных программистов изменили свою жизнь наполовину, многие люди используют только C. Поэтому пример кода в этой статье реализован на языке Си. В качестве вводного эссе код, приведенный в этой статье, более нацелен на демонстративность и максимально читабельный. Таким образом, код в этой статье не является наиболее эффективной реализацией, но он достаточно быстр для общих приложений.

Говоря о паритете

Так называемая проверка процесса связи относится к добавлению некоторой дополнительной информации после данных связи и использованию этой дополнительной информации, чтобы определить, совпадают ли принятые данные с отправленными данными. Например, последовательная связь RS232 может устанавливать бит четности.Так так называемая проверка четности заключается в добавлении бита после каждого отправленного байта, чтобы число 1 в каждом байте было нечетным или четным. Например, байт, который мы хотим отправить, равен 0x1a, а двоичное представление — 0001 1010.

При нечетной четности после данных добавляется 0, и данные становятся 0001 1010 0. Число 1 в данных нечетное (3)

При четной четности после данных добавляется 1, и данные становятся 0001 1010 1. Число 1 в данных является четным (4)

Накопление и проверка

Другим распространенным методом проверки является накопление и проверка. Существует много способов реализовать так называемое накопление и контрольную сумму, наиболее распространенным из которых является добавление байта данных контрольной суммы в конец коммуникационного пакета. Содержимое этого байта является побайтной накопленной суммой всех данных в предыдущем пакете данных, которые игнорируются. Возьмите следующий пример:

Информация, которую мы хотим передать: 6, 23, 4

Пакеты данных с добавленной контрольной суммой: 6, 23, 4, 33

Здесь 33 — контрольная сумма первых трех байтов. После получения всех данных приемник выполняет те же вычисления накопления для первых трех данных.Если накопление совпадает с последним байтом, переданные данные считаются безошибочными.

Накопление и проверка широко используются, потому что они просты в реализации. Тем не менее, возможность обнаружения ошибок этого метода проверки также является довольно общей: для однобайтовой контрольной суммы существует вероятность 1/256 того, что исходные неверные данные связи неверно оценены как правильные данные. Причина введения этого вида проверки здесь заключается в том, что проверка CRC такая же, как накопление и проверка в форме переданных данных, и может быть выражена как: байт проверки данных связи (также может быть несколькими байтами)

Знакомство с алгоритмом CRC

Основная идея алгоритма CRC заключается в обработке переданных данных как длинного числа. Разделите это число на другое число. Полученный остаток добавляется в качестве контрольных данных к исходным данным. Возьмите данные в приведенном выше примере в качестве примера:

6, 23, 4 можно рассматривать как двоичное число: 0000011000010111 00000010

Если дивиденд равен 9, двоичное представление: 1001

Операция деления может быть выражена как:

Как видите, последний остаток равен 1. Если мы используем этот остаток в качестве контрольной суммы, переданные данные: 6, 23, 4, 1

Алгоритм CRC похож на этот процесс, но это не обычное деление в приведенном выше примере. В алгоритме CRC поток двоичных данных используется в качестве коэффициента многочлена, а затем выполняется умножение и деление многочлена. Давайте возьмем пример.

Например, у нас есть два двоичных числа: 1101 и 1011.

1101 связан со следующим полиномом: 1x 3 +1x 2 +0x 1 +1x 0 =x 3 +x 2 +x 0

1011 связан со следующим полиномом: 1x 3 +0x 2 +1x 1 +1x 0 =x 3 +x 1 +x 0

Умножение двух полиномов: (х 3 +x 2 +x 0 )(x 3 +x 1 +x 0 )=x 6 +x 5 +x 4 +x 3 +x 3 +x 3 +x 2 +x 1 +x 0

После получения результатов при объединении аналогичных терминов используется операция по модулю 2. То есть умножение и деление используют обычное полиномиальное умножение и деление, а сложение и вычитание используют операцию по модулю 2. Так называемая операция по модулю 2 состоит в том, чтобы разделить результат на 2 и взять остаток. Например, 3 mod 2 = 1. Таким образом, последний полином, полученный выше: 6 +x 5 +x 4 +x 3 +x 2 +x 1 +x 0 Соответствующее двоичное число: 111111

Сложение и вычитание с использованием операции по модулю 2 фактически стало операцией, которую мы обычно называем операцией XOR:

Полином полдня был упомянут выше, фактически, даже если не ввести понятие полиномиального умножения и деления, эти операции являются специальными. Просто почти во всей литературе, где объясняется алгоритм CRC, упоминаются полиномы, поэтому здесь также написана простая базовая концепция. Однако всегда очень сложно использовать этот вид полиномиального выражения, а в следующем объяснении мы попытаемся использовать более сжатый способ написания.

Операция деления аналогична приведенной выше концепции умножения, или место, где встречаются сложение и вычитание, заменяется операцией XOR. Вот пример:

Данные для передачи: 1101011011

Делитель установлен на: 10011

Перед расчетом заполните исходные данные 4 0: 11010110110000. Причина, по которой вы хотите добавить 0, будет объяснена позже.

Из этого примера видно, что после сложения и вычитания по модулю 2 нет необходимости рассматривать проблему заимствования, поэтому деление становится проще. Полученный остаток — контрольное слово CRC. Чтобы выполнить операцию CRC, то есть эту специальную операцию деления, необходимо указать дивиденд.В алгоритме CRC этот дивиденд имеет собственное имя, называемое «полином-генератор». Выбор генераторных полиномов — очень сложная проблема, и если выбор не будет хорошим, вероятность обнаружения ошибок будет намного ниже. К счастью, эта проблема давно изучается специалистами, для нас, пользователей, пока используются готовые результаты.

Наиболее часто используемые генераторы полиномов следующие:

CRC8=X 8 +X 5 +X 4 +X 0

CRC-CCITT=X 16 +X 12 +X 5 +X 0

CRC16=X 16 +X 15 +X 2 +X 0

CRC12=X 12 +X 11 +X 3 +X 2 +X 0

CRC32=X 32 +X 26 +X 23 +X 22 +X 16 +X 12 +X 11 +X 10 +X 8 +X 7 +X 5 +X 4 +X 2 +X 1 +X 0

Важно отметить, что полиномы-генераторы, упомянутые в литературе, часто говорят о ширине полинома (ширина, сокращенно обозначается как W) .Этой шириной бит является не количество бит двоичного числа, соответствующего полиному, а количество бит минус 1. Например, полином генератора с шириной в 8 бит, используемый в CRC8, фактически соответствует девяти двоичным числам: 100110001. Кроме того, полиномиальные и двоичные представления громоздки и неудобны в общении, поэтому шестнадцатеричное сокращение часто используется в литературе для их представления, потому что самый старший бит полинома генератора должен быть 1, а позиция самого старшего бита может быть известна по ширине бита. В сокращенной формуле старшая единица удаляется равномерно, например, полином-генератор CRC32 сокращенно обозначается как 04C11DB7, что фактически представляет 104C11DB7. Конечно, в дополнение к удобству такого короткого примечания, это также полезно в программировании вычислений.

Для вышеприведенного примера ширина бита равна 4 (W = 4). В соответствии с требованиями алгоритма CRC, W нули должны быть заполнены после исходных данных перед вычислением, то есть четыре ноля.

Существует два вида генераторных полиномов (CRC1) с шириной бита W = 1, которые равны X 1 И х 1 +X 0 Читатель может доказать для себя, что 10 соответствует нечетной проверке по четности, а 11 соответствует четной проверке. Поэтому, как мы уже писали здесь, мы знаем, что четность на самом деле является частным случаем CRC, поэтому я хочу начать с четности.

Программная реализация алгоритма CRC

Сказав так много, это, наконец, основная часть. Из предыдущего введения мы знаем, что ядром проверки CRC является реализация операции деления без заимствования. Ниже приведен пример, иллюстрирующий реализацию проверки CRC.

Предположим, что наш полином-генератор: 100110001 (сокращенно 0x31), то есть CRC-8

Этапы расчета следующие:

(1) Регистру CRC (8 бит, на 1 бит меньше, чем полином генератора) присваивается начальное значение 0

(2) Добавьте 8 нулей после потока информации, который будет передан

(3) Пока (данные не обработаны)

(5) Если (Первый бит регистра CRC равен 1)

（6） reg = reg XOR 0x31

(7) Регистр CRC сдвигается на один бит влево, и новые данные считываются в позиции 0 бит регистра CRC.

(9) Регистр CRC — это остаток, который нам требуется.

Как просто посчитать контрольную сумму CRC (CRC32 — CRC16 — CRC8)

В интернете существует большое количество вариантов расчёта контрольной суммы CRC. Но что же собственно такое контрольная сумма и почему она рассчитывается именно так? Давайте разбираться.

Как просто посчитать контрольную сумму CRC (CRC32 - CRC16 - CRC8)

Статьи по теме:

Как просто посчитать контрольную сумму CRC (CRC32 — CRC16 — CRC8)
Как узнать контрольную сумму файла
Как проверить контрольную сумму файла

Инструкция

Для начала давайте немного разберёмся в теории. Итак, что же такое CRC? Если кратко, это одна из разновидностей подсчёта контрольной суммы. Контрольная сумма — это метод проверки целостности принятой информации на стороне приёмника при передаче по каналам связи. Например, одна из простейших проверок — использование бита чётности.

Это когда суммируются все биты передаваемого сообщения, и если сумма оказывается чётной, то в конец сообщения добавляется 0, если нечётной — то 1. При приёме также подсчитывается сумма битов сообщения, и сравнивается с принятым битом чётности. Если они отличаются, значит при передаче возникли ошибки, и передаваемая информация была искажена.

Но такой способ определения наличия ошибок — очень неинформативный и срабатывает не всегда, т.к. при искажении нескольких битов сообщения, чётность суммы может не измениться. Поэтому существует множество более «продвинутых» проверок, в том числе CRC.

По сути, CRC — это не сумма, а результат деления некого объёма информации (информационного сообщения) на константу, а точнее — остаток от деления сообщения на константу. Тем не менее, CRC исторически также называют «контрольная сумма». В значение CRC вносит вклад каждый бит сообщения. То есть, если хотя бы один бит исходного сообщения изменится при передаче, контрольная сумма тоже изменится, причём существенно. Это большой плюс такой проверки, так как он позволяет однозначно определить, исказилось исходное сообщение при передаче или нет.

Прежде чем приступать к вычислению CRC, понадобится ещё немного теории.
Что такое исходное сообщение должно быть понятно. Это непрерывная последовательность битов произвольной длины.

Что за константа, на которую мы должны делить исходное сообщение? Это некоторое число также любой длины, но обычно используются числа, кратные 1 байту — 8, 16 и 32 бита. Просто так легче считать, ведь компьютеры работают именно с байтами, а не с битами.

Константу-делитель обычно записывают в виде полинома (многочлена) вот таким образом: x^8 + x^2 + x^1 + x^0. Здесь степень числа «x» означает позицию бита-единицы в числе, начиная с нулевой, а старший разряд указывает на степень полинома и отбрасывается при интерпретации числа. То есть записанное ранее число — это не что иное как (1)00000111 в двоичной системе счисления, или 7 в десятичной. В скобках я указал подразумеваемый старший разряд числа.
Вот ещё пример: x^16 + x^15 + x^2 + x^0 = (1)1000000000000101″ = 0x8005 = 32773.
Обычно используются некие стандартные многочлены для разных типов CRC.

Так как же считать контрольную сумму? Существует базовый метод — деление сообщения на полином «в лоб» — и его модификации в целях уменьшения количества вычислений и, соответственно, ускорения расчёта CRC. Мы рассмотрим именно базовый метод.

В общем виде, деление числа на многочлен выполняется по такому алгоритму:
1) создаётся массив (регистр), заполненный нулями, равный по длине разрядности полинома;
2) исходное сообщение дополняется нулями в младших разрядах, в количестве, равном числу разрядов полинома;
3) в младший разряд регистра заносится один старший бит сообщения, а из старшего разряда регистра выдвигается один бит;
4) если выдвинутый бит равен «1», то производится инверсия битов (операция XOR, исключающее ИЛИ) в тех разрядах регистра, которые соответствуют единицам в полиноме;
5) если в сообщении ещё есть биты, переходим к шагу 3);
6) когда все биты сообщения поступили в регистр и были обработаны этим алгоритмом, в регистре остаётся остаток от деления, который и является контрольной суммой CRC.

Рисунок иллюстрирует деление исходной последовательности битов на число (1)00000111, или многочлен x^8 + x^2 + x^1 + x^0.

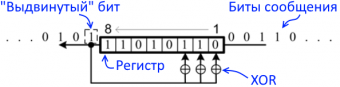
Схематичное представление вычисления CRC

Осталась ещё пара дополнительных штрихов. Как вы могли заметить, сообщение можно разделить на любое число. Как его выбрать? Существует ряд стандартных полиномов, которые используются при вычислении CRC. Например, для CRC32 это может быть число 0x04C11DB7, а для CRC16 это может быть 0x8005.
Кроме того, в регистр в начале вычислений можно записать не нули, а какое-то другое число.

Также при расчётах непосредственно перед выдачей финальную контрольную сумму CRC могут делить на какое-то другое число.

И последнее. Байты сообщения при записи в регистр могут помещаться как старшим битом «вперёд», так и наоборот, младшим.

На основании всего вышеизложенного, давайте напишем функцию на языке Basic .NET, которая будет рассчитывать контрольную сумму CRC, принимая ряд параметров, которые я описал выше, и возвращая значение CRC в виде 32-разрядного беззнакового числа.

Public Shared Function GetCrc(ByVal bytes As Byte(), ByVal poly As UInteger, Optional ByVal width As Integer = 32, Optional ByVal initReg As UInteger = HFFFFFFFFUI, Optional ByVal reverseBytes As Boolean = True, Optional ByVal reverseCrc As Boolean = True) As UInteger

Dim widthInBytes As Integer = width 8

‘Дополняем сообщение width нулями (расчёт в байтах):
ReDim Preserve bytes(bytes.Length — 1 + widthInBytes)

‘Создаём очередь битов из сообщения:
Dim msgFifo As New Queue(Of Boolean)(bytes.Count * 8 — 1)
For Each b As Byte In bytes
Dim ba As New BitArray()
If reverseBytes Then
For i As Integer = 0 To 7
msgFifo.Enqueue(ba(i))
Next
Else
For i As Integer = 7 To 0 Step -1
msgFifo.Enqueue(ba(i))
Next
End If
Next

‘Создаём очередь из битов начального заполнения регистра:
Dim initBytes As Byte() = BitConverter.GetBytes(initReg)
Dim initBytesReversed As IEnumerable(Of Byte) = (From b As Byte In initBytes Take widthInBytes).Reverse
Dim initFifo As New Queue(Of Boolean)(width — 1)
For Each b As Byte In initBytesReversed
Dim ba As New BitArray()
If Not reverseBytes Then
For i As Integer = 0 To 7
initFifo.Enqueue(ba(i))
Next
Else
For i As Integer = 7 To 0 Step -1
initFifo.Enqueue(ba(i))
Next
End If
Next

‘Сдвиг и XOR:
Dim register As UInteger = 0 ‘заполняем width-разрядный регистр нулями.
Do While msgFifo.Count > 0

Dim poppedBit As Integer = CInt(register >> (width — 1)) And 1 ‘определить перед сдвигом регистра.

Dim shiftedBit As Byte = Convert.ToByte(msgFifo.Dequeue)
If initFifo.Count > 0 Then
Dim b As Byte = Convert.ToByte(initFifo.Dequeue)
shiftedBit = shiftedBit Xor b
End If

If poppedBit = 1 Then
register = register Xor poly
End If
Loop

‘Финальные преобразования:
Dim crc As UInteger = register ‘Регистр содержит остаток от деления == контрольную сумму.
If reverseCrc Then
crc = reflect(crc, width)
End If
crc = crc Xor finalXor
crc = crc And (> (32 — width)) ‘маскируем младшие разряды.

Источник: www.kakprosto.ru