Что является результатом решения задачи оптимизации производственной программы

Аннотация научной статьи по экономике и бизнесу, автор научной работы — Волощук С. А., Гулакова С. А.

Из экономических показателей выбран критерий (прибыль от реализации товарной продукции) для оптимизации производственной программы промышленного предприятия. Сформулирована модель оптимизации производственной программы в виде задачи линейного программирования.

i Надоели баннеры? Вы всегда можете отключить рекламу.

Похожие темы научных работ по экономике и бизнесу , автор научной работы — Волощук С. А., Гулакова С. А.

Планирование затрат на машиностроительных предприятиях с использованием оптимизационных задач
Производственный анализ: вопросы оптимизации продуктовых программ
Методология анализа оптимизации ассортимента продукции на долгосрочную перспект
Инновационное обеспечение оптимизации производства на предприятиях

Подходы к формированию производственной программы для предприятий с дискретным механосборочным типом производства¹

i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
i Надоели баннеры? Вы всегда можете отключить рекламу.

Текст научной работы на тему «Оптимизация производственной программы промышленного предприятия»

В1СНИК ПРИАЗОВСЬКОГО ДЕРЖАВНОГО ТЕХН1ЧНОГО УН1ВЕРСИТЕТУ 2008 р. Вип. № 18

Решение оптимизационных задач — часть 1 (задача оптимизации производства)

Волощук В.А.1, Гулакова С.А.2

ОПТИМИЗАЦИЯ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ПРОМЫШЛЕННОГО ПРЕДПРИЯТИЯ

Из экономических показателей выбран критерий (прибыль от реализации товарной продукции) для оптимизации производственной программы промышленного предприятия. Сформулирована модель оптимизации производственной программы в виде задачи линейного программирования.

Опыт многих преуспевающих предприятий развитых промышленных стран показывает, что в условиях рынка с его жесткой конкуренцией планирование производственно-хозяйственной деятельности предприятий является важнейшим условием их выживаемости, экономического роста и процветания. Одним из наиболее эффективных средств планирования, позволяющим организовать производство с нацеленностью его на максимальную эффективность и, одновременно, на удовлетворение потребительского спроса, является оптимизация производственной программы. Решение задач по оптимизации производственной программы начинается с обоснования выбора критерия оптимальности, определения целевой функции и ограничений задачи.

В разное время решением вопросов оптимизации планов производства занимались отечественные и зарубежные исследователи. Так, Глухов В.В. в своей работе затронул проблемы анализа оптимизационных методов решения экономических задач, связанных с выбором оптимальной производственной программы [1]. Савицкая Г.В. занималась вопросами обоснования оптимальной структуры товарного выпуска с учетом ограничений на ресурсы [2]. Немецкий ученый Фольмут Х.И. рассматривал проблемы оптимизации программы производства и продаж методом устранения «узких мест» [3]. Проведенный анализ экономической литературы показывает недостаточность разработки задач по оптимизации производственной программы как теоретически, так и практически.

Целочисленные задачи оптимизации

Целью данной работы является анализ экономических критериев, выбор наиболее приемлемого критерия оптимальности, целевой функции и ограничений для решения задачи оптимизации производственной программы промышленного предприятия.

Экономические критерии — экономические показатели, определяющие сущность конкретного явления или объекта. Они являются факторами, влияющими на достижение того или иного экономического результата, обычно выраженного отдельным комплексным показателем [1]. Применительно к понятию «производственная программа» экономические критерии — факторы, в совокупности обеспечивающие достижение определённого объёма производства с соответствующими характеристиками по ассортименту и качеству продукции. Экономический принцип требует, чтобы сочетание производственных показателей при этом было оптимальным, то есть обеспечивающим наибольший экономический эффект.

Под оптимальной производственной программой понимается такое сочетание и степень использования факторов производства, а также структура ассортимента продукции, которые обеспечивают максимальную экономическую эффективность производства в сложившихся условиях хозяйствования. То есть целью производственной программы, с точки зрения оптимальности, является получение наибольшего экономического эффекта по отношению к объёму затраченных ресурсов.

Среди большого числа количественных и качественных экономических показателей, характеризующих эффективность использования производственных ресурсов, необходимо выбрать основной комплексный критерий, который наиболее полно отражает все экономические элементы производственного процесса. На рис. 1 представлена обобщённая структура показателей, характеризующих производственную программу промышленного предприятия.

Основные показатели производственной программы

— Объем товарной/реализованной продукции

— Общая сумма затрат на производство

— Прибыль от реализации товарной продукции

Рис. 1 — Основные показатели производственной программы

Рп = (Цед — Сед) / Сед , (1)

где Рп — рентабельность продукции; Цед — цена единицы продукции; Сед — себестоимость единицы продукции. Рпр = Преал / (Соф + Собф), (2)

где Рпр — рентабельность производства;

Преал — прибыль от реализации продукции; Соф — стоимость основных фондов; Собф — стоимость оборотных фондов.

Как видно из рис. 1 производственная программа может быть охарактеризована с двух сторон: масштаб производства и эффективность производства. Первая характеристика представлена абсолютными показателями: объём валовой продукции, объём товарной продукции, объём отгруженной продукции, затраты на производство продукции, прибыль от реализации товарной продукции.

Показатели объем производства, объем товарной и реализованной продукции описывают объем и структуру валовой, товарной и реализованной продукции, но не затрагивают затратную составляющую производства и результатов хозяйственной деятельности. Показатели общая сумма затрат на производство и себестоимость продукции наоборот описывают лишь затратную часть производства, но не касаются объемов и результатов производства. Последний из перечисленных показателей является результативным и, поэтому, основным показателем масштаба производства, отражающим экономический эффект от реализации производственной программы и определяемым как разность между стоимостью товарной продукции и её себестоимостью.

Другая часть критериев — показатели эффективности производства, представленные в правой части рис. 1, являются относительными и отражают относительную величину получаемого эффекта, то есть эффективность. Это показатели рентабельности продукции и рентабельности производства.

По показателю рентабельность продукции можно судить о рентабельности производства отдельных видов продукции, но не о всей производственной программе. Показатель рентабельность производства является комплексным показателем с позиции формирования оптимальной производственной программы.

При разработке программы оптимизации выпускаемой продукции необходимо прибегать к упрощению модели, так как описать на языке программирования сложную экономическую систему даже для небольших предприятий весьма сложно. Поэтому использование показателя рентабельности производства в качестве критерия оптимальности затруднительно. Кроме вышесказанного, показатели эффективности производства не позволяют максимизировать суммарную прибыль от реализации продукции. Это продемонстрировано на количественном примере в работе Э. Голдрэтта [4].

Таким образом, результаты формирования производственной программы в наибольшей степени проявляются в показателях объёма, структуры товарной продукции и затрат на товарный выпуск. Поэтому наиболее приемлемым показателем оптимальности производственной программы является показатель расчётной прибыли от реализации товарной продукции, рассчитываемый по формуле (3):

где Птп — прибыль от реализации товарной продукции; ТП — товарная продукция в стоимостном выражении; Стп — полная себестоимость товарной продукции.

Теперь остановимся подробнее на методах используемых при оптимизации производственной программы. Как известно, под оптимизацией в широком смысле понимается выбор наилучшего по принятому критерию решения с учётом имеющихся ограничений [5, 6]. В оптимизационной задаче присутствуют, в общем случае, следующие элементы:

— показатель оптимальности (эффективности), или критерий оптимальности — это операционное представление цели, которую исследователь стремится достичь;

— варьируемые параметры — величины, влияющие на значение показателя оптимальности и определяющие его величину;

— ограничения — зависимости, определяющие границы варьирования параметрами.

Исследование и оптимизация сложной системы предусматривает:

— во-первых, построение модели, адекватно отражающей наиболее существенные свойства системы;

— во-вторых, постановку задачи оптимизации;

— в-третьих, выбор метода оптимизации в соответствии с особенностями модели и поставленной задачи.

Из всех видов моделирования наибольшее распространение при исследовании и оптимизации экономических систем получило математическое моделирование. Математическая постановка задачи оптимизации сводится к следующим этапам:

1) описание варьируемых параметров через переменные: хь х2, . хп;

2) представление критерия оптимизации в форме целевой функции выбранных переменных:

3) формализация ограничений в виде функций выбранных переменных: в! = ^(хь х2, . х„); в2 = £>(хь х2, . х„); . ; От = ^(хь х2, . х„).

В зависимости от вида полученных в модели функциональных зависимостей и цели исследования применяются различные методы оптимизации (иначе, методы исследования операций). Из всего многообразия применяемых методов остановимся лишь на тех из них, которые имеют отношение к предмету нашего исследования, то есть используются при оптимизации производственной программы.

Одной из наиболее распространённых математических моделей, применяемых при оптимизации производственной программы производственного предприятия, является модель линейного программирования.

Выделяют следующие особенности задач линейного программирования:

а) показатель эффективности (целевая функция) линейно зависит от элементов решения ХЬ Х2, . хп;

б) ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно хь х2, . хп.

Широкое применение данного метода при оптимизации экономических систем объясняется линейным характером большинства экономических зависимостей: «. во многих задачах практики «расходы» и «доходы» линейно зависят от количества закупленных или утилизированных средств» [5].

В общем виде наиболее распространённая модель формирования оптимальной программы включает целевую функцию (4):

Б = С1Х1 + с2х2 + . + спхп —> тах(гшп) (4)

и систему ограничений (5) и (6):

ат1Х1 + ат2х2 + . + атпХп < Ьт,

где Б — суммарное значение показателя, принятого в качестве критерия оптимальности;

п — число наименований изготовляемых изделий;

Xj — количество изделий j -того наименования;

^ — оценка изделия j -того наименования в соответствии с критерием оптимальности;

ау — затраты ¿-того ресурса на изготовление изделия j -того наименования;

Ь; — располагаемая величина ¿-того ресурса;

N111111. ЫГТ,;|Х — допустимые пределы выпуска изделий j-того наименования.

Минимальный выпуск изделий может определяться заключёнными контрактами на поставку продукции или критическим объёмом продаж, максимальный — потребностью рынка с учётом планируемой доли организации.

Будем полагать, что в результате маркетинговых исследований получены выборки прогнозных значений следующих показателей:

Цу = | Ц,| 1 .Ц,|2. . Ц||,,| — цена^го вида продукции из ¿-го вида сырья; Су = [Су 1, С. . СуП] — себестоимость выпуска j-oгo вида продукции из ¿-го вида сырья; ТЧшах = [1Чтах 1, Ыт»х 2, • • •, п] — максимальный объем спроса на продукцию j-ого вида (с учетом

возможного выпуска его конкурентами); 12, •••, Nmln п] — обязательный объем выпуска продукции _)-ого вида (при наличии долгосрочных договоров); т — общее количество видов сырья; п — число наименований изготовляемых изделий;

8 шах готах етах стах | ■

! = [Ь и . Ь ¡2. Ь ,Т11 — максимально возможный объем поставок 1-го вида сырья. Кроме того, считаем известными следующие параметры производственного процесса: Я — общее количество оборудования г-ш вида;

Мфг — среднегодовая производственная мощность оборудования г-го вида; Ь,, — выход продукции j-го вида из сырья из ¿-го вида сырья;

а||г — время производства продукции_]-го вида из сырья ¿-го вида на оборудовании г-го вида.

В качестве критерия оптимальности, как определено выше, следует рассматривать средне значение или математическое ожидание прибыли от товарного выпуска. В итоге получим эко-номико-математическую модель в виде (7):

М(Цг] ) — математическое ожидание (среднее значение) цены j-го вида продукции из i-ro вида сырья;

M (Сj>) — математическое ожидание (среднее значение) себестоимости выпуска j-ro вида продукции из i-ro вида сырья; M(NITlii ; ,) — математическое ожидание (среднее значение) максимального объема спроса на продукцию j-ro вида из i-ro вида сырья (с учетом возможного выпуска его конкурентами); M(Nmm ¡j) — математическое ожидание (среднее значение) обязательного объема выпуска продукции j-ro вида из i-ro вида сырья (при наличии долгосрочных договоров);

M(S™X ) — математическое ожидание (среднее значение) максимально возможного объема по ставок i-ro вида сырья.

Методы решения задач линейного программирования достаточно хорошо разработаны. В результате ее решения получаем как оптимальные объемы выпуска различной продукции xlj5 так и потребные для этого объемы сырья.

Данная экономико-математическая модель характеризует производственную программу при колебаниях спроса (N111114,,). возможных поставках сырья (S111114,), цены готовой продукции (Цм) и затратах на ее выпуск (Су).

Дальнейшие исследования в данном направлении предполагают разработку и внедрение методики использования предложенной модели формирования оптимальной производственной программы для планирования производственной программы промышленного предприятия.

1. Проведенный анализ позволил обосновать выбор показателя прибыли от реализации товарной продукции в качестве критерия оптимальности производственной программы промышленного предприятия. В дальнейшем этот показатель будет использован при построении экономико-математической модели формирования оптимальной производственной программы.

2. Формирование производственной программы следует проводить на основе решения прямой задачи линейного программирования, в ходе которой объемы выпуска продукции должны определяться по видам готовой продукции с учетом ограничений по объемам доступного сырья, производственных мощностей, трудовых ресурсов, спросу на готовую продукцию, необходимости выполнения обязательных заказов.

1. Глухое В. В. Экономико-математические методы и модели в планировании и управлении на металлургических предприятиях: Учебное пособие для вузов / В.В. Глухое, А.А. Спасов. -М.: Металлургия, 1992. — 223 с.

2. Савицкая Г.В. Анализ хозяйственной деятельности предприятия: Учебное пособие / Г.В. Савицкая. — Минск: ООО «Новое знание», 2001. — 704 с.

3. Фолъмут Х.И. Инструменты контроллинга от А до Я / Х.И. Фолъмут. — М.: Финансы и статистика, 1998. — 288 с.

4. Goldratt Eliyahu M. The haystack syndrome: sifting information out of the data océan / E.M. Goldratt. — NY.: North River Press, 1990. — 262 p.

5. Вентцелъ E.C. Исследование операций: задачи, принципы, методология. / Е.С. Вентцелъ. -М.: Наука, 1988.-208 с.

6. Канторович Л.В. Оптимальные решения в экономике / Л.В. Канторович, А.Б. Горстко. — М.: Наука, 1972.-231 с.

Рецензент: Н.Г. Белопольский д-р экон. наук, проф., ПГТУ

i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Статья поступила 10.03.2008

Источник: cyberleninka.ru

1.2. Оптимизация производственной программы

При осуществлении производственного процесса предприятие использует различные ресурсы. Эти ресурсы можно подразделять на определенные категории. Например, производственная мощность, материалы, труд. При отсутствии жесткого централизованного пла­нирования возможна разработка множества производственных про­грамм при использовании одних и тех же производственных ресур­сов. В таких условиях выбор наилучшего варианта производствен­ной программы становится важнейшей задачей руководства предприя­тия.

Задача оптимизации производственной программы может быть сформулирована в двух вариантах:

— определение производственной программы, позволяющей по­лучить наилучший результат (максимальный доход, прибыль) при заданных объемах ресурсов;

— определение производственной программы, обеспечивающей получение заданного объема производства при наименьших затра­тах.

В лабораторной работе решается задача получения максималь­ного дохода предприятия при заданных объемах производственных ресурсов. Задача решается при следующих условиях:

— номенклатура выпускаемой предприятием продукции вклю­чает 3 наименования;

— в производственном процессе используется 2 вида ресур­сов: металл и труд; объем ресурсов, которым располагает пред­приятие, ограничен;

— вся продукция, производимая предприятием в рассматриваемом периоде, реализуется в том же периоде; остатков на его на­чало и конец предприятие не имеет;

— цены на продукцию в рассматриваемом периоде остаются не­изменными.

2. Математическая постановка задачи и метод её решения

2.1. Формализация задачи

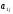
Пусть — нормативная трудоемкость изготовления одного изделияj-го типа (чел.-час);

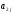
– нормативная металлоемкость одного изделия j-го типа (кг);

в1 – суммарная трудоемкость производственной программы предприятия (чел.-час);

в2 – суммарная металлоемкость производственной программы предприятия (кг);

Сj – отпускная цена одного изделия j- го типа (руб.);

Хj– объем производства (количество) изделий j-го типа (шт.);

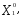
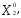
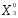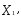
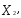
Необходимо определить оптимальную производственную программу предприятия Х 0 = (), т.е. такое распределение объемов производства Х = (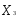), при котором достигается наибольший доход:

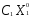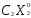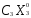++=max (++),

().

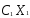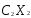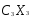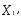
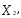
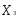При ограничениях на трудоемкость и металлоемкость:

+ +=;

+ +=.

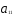
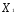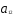
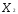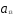
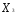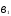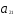
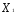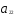
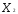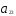
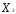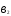В настоящей работе мы будем предполагать следующее:

— нормы трудоемкости и металлоемкости строго положительны:

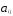
> 0; i = 1,2; j = 1,2,3;

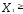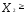— объемы производства неотрицательны 0,0,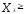0, так что если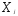= 0, то изделиеj-го типа не включается в производственную программу, i = 1, 2, 3;

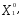
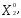
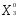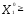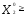— оптимальная производственная программа (), где0,0,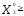0 существует, т.е. ограничения трудоемкости и металлоемкости сбалансированы;

— ограничения по трудоемкости и металлоемкости независимы в том смысле, что линейно независима любая пара из векторов (,), (,), (,).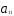

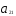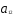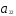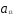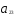В контрольном примере, рассмотренном ниже, а также во всех вариантах заданий, указанные предположения выполняются в реальных производственных программах.

2.2. Метод решения

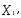
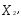
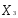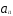
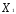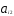
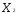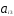
В пространстве переменных () каждое из ограничений вида++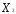=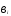по трудоемкости или металлоемкости определяет плоскость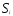, проходящую через точки:

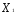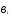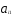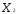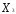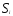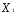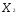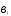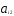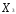(=/,= 0,= 0),

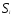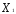(= 0,=/,= 0),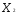

(= 0,= 0,=/),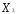

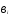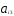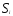Пример изображения этих плоскостей приведен на рис. 1.

Точки, лежащие на линии пересечения плоскосте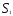й и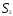, удовлетворяют ограничениям по трудоемкости и металлоемкости одновременно. При этом линия пересечения существует в силу принятого предположения об отсутствии взаимной зависимости ограничений.

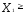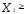Наконец, условия 0,0,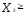0 определяют отрезок линии пересечения плоскосте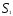йи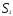, лежащий между координатными плоскостями. Такой отрезок тоже существует в силу сбалансированности ограничений. Точки отрезка (и только они) удовлетворяют всем ограничениям и предположениям, принятым в задаче.

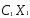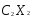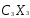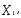
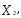
Целевая функция y = ++является линейной по переменным (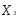) и, следовательно, достигает своего наибольшего и наименьшего значения на концах построенного отрезка, один из которых и является решением задачи.

Источник: studfile.net

Задача оптимизации производственной программы предприятия

Предприятие выпускает несколько видов продукции П , , 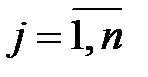имея ограниченный запас ресурсов Р , . Известны нормы затрат ресурса Р на производство единицы продукции П – . Требуется найти такой план производства продукции, который обеспечивает максимум эффекта от выпуска (максимум выручки от реализации, минимум затрат), если — эффективность единицы продукции (например, цена).

Сформулируем математическую модель задачи. Определим переменные модели: – объем производства продукции -го вида .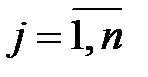

В этих обозначениях задача оптимизации производственной программы запишется в следующем виде:

максимизируется выручка от реализации

при ограничениях на запас -го ресурса:

, ,

и условии неотрицательности переменных:

, .

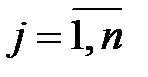Пример. Пусть предприятие выпускает два вида изделий и располагает следующими ресурсами (в расчете на сутки): фонд рабочего времени производственных рабочих — 780 чел.-ч, фонд сырья — 850 ед., электроэнергии –790 ед. Нормы расхода ресурсов в расчете на одно изделие представлены в таблице.

Ресурс	Изделие
I вид	II вид
Рабочее время, чел.-ч
Сырье, ед.
Электроэнергия, ед.

Цена изделия I вида — 6 у.е., II вида — 7 у.е.

Требуется определить оптимальную производственную программу предприятия с учетом получения максимальной прибыли.

Решение. Математическое описание исследуемого объекта или процесса начинается с выбора переменных модели. Так как в рассматриваемом примере требуется построить модель для определения оптимальной структуры производственной программы по выпуску изделий I, и II видов, введем переменные: – суточный объем производства продукции I вида, – суточный объем производства продукции II вида.

Запишем ограничения на ресурсы.

Рабочее время. Так как нормы расхода рабочего времени для производства единицы продукции I и II вида составляют 2 чел.-ч. и 3 чел.-ч соответственно, то для производства изделий I вида в объеме , изделий II вида в объеме требуется (чел.-ч). С другой стороны, объем использования оборудования не должен превышать имеющегося суточного фонда рабочего времени – 780 чел.-ч. Таким образом, получаем ограничение:

.

Аналогично составляются ограничения для оставшихся видов ресурсов.

Сырье: .

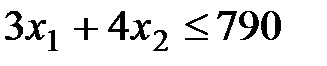
Электроэнергия: .

Кроме того, объем производства изделий каждого вида не может быть отрицательным: , .

В данном примере целью управления (критерием качества) является получение максимальной прибыли, что приводит к экономико-математической оптимизационной модели – задаче максимизации целевой функции:

.

,

,

,

, .

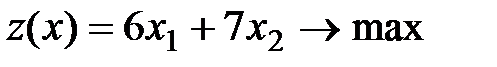
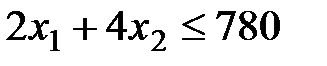
Сформулированная модель является задачей линейного программирования.

Модели межотраслевого баланса

Основные понятия

Под балансовой моделью понимается система уравнений, каждое из которых выражает требование баланса между производимым отдельными экономическими объектами количеством продукции и совокупной потребностью в этой продукции. Балансовый метод – это метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них.

Примерами балансовых соответствий могут быть: соответствие наличия рабочей силы и количества рабочих мест; платежеспособного спроса населения и предложения товаров и услуг и т.д. При этом соответствие понимается либо как равенство, либо (менее жестко) как достаточность ресурсов для покрытия потребности и, следовательно, наличие некоторого резерва.

Балансовые модели строятся в виде числовых матриц, поэтому они относятся к матричным экономико-математическим моделям.

Некоторые виды балансовых моделей:

1. Частные материальные, трудовые и финансовые балансы для народного хозяйства и отдельных отраслей.

2. Межотраслевые балансы.

3. Матричные финансовые планы предприятий и фирм.

Совокупный общественный продукт – масса произведенных или планируемых к производству материально-вещественных благ и услуг. В стоимостном выражении совокупный общественный продукт делится на: перенесенную стоимость (износ средств труда и расход предметов труда); вновь созданную стоимость, то есть национальный доход.

В натуральном межотраслевом балансе отражается движение совокупного общественного продукта по его материально-вещественному составу.

Чистые (технологические) отрасли – это некоторые условные отрасли, которые объединяют все производство данного вида продукта независимо от ведомственной подчиненности субъектов хозяйствования, их производящих.

Межотраслевые балансы строятся на основе следующих предположений:

1. Каждая отрасль производит только один продукт, то есть выделение отраслей производится не по принципу однородности предприятий, а по принципу однородности продукта. По этой причине межотраслевые балансы иногда еще называют межпродуктовыми балансами;

2. Каждая отрасль как бы имеет только одну технологию производства продукции, которая характеризуется средневзвешенными коэффициентами затрат. Эти коэффициенты затрат отражают взаимосвязь между отраслями и являются отраслевыми нормативами затрат.

В общем виде межотраслевой баланс состоит из четырех разделов, которые называются квадрантами:

I	II
III	IV

Основным является первый квадрант, так как его данные используются во всех расчетах и являются их основой. Во втором квадранте характеризуется непроизводственная сфера. В I и III-м квадрантах характеризуются текущие затраты материального производства. Во II и IV-м – показывается использование продукции за пределами текущего производственного цикла. Иначе говоря, процессы накопления, непроизводственного потребления и вывода продукции за пределы региона, что в целом называется конечным потреблением.

При записи соотношений могут использоваться как натуральные (тонны, штуки, киловатт-часы и т. п.), так и стоимостные единицы измерения указанных величин, поэтому различают натуральный и стоимостной балансы.

Источник: cyberpedia.su