Структурированные программы следует писать таким образом, чтобы они легко читались и были понятны. На первый взгляд может показаться, что структурированную программу написать не намного труднее, чем неструктурированную. [2]
Структурированная программа сама по себе не является гарантией того, что разработка будет выполнена успешно. Структурное программирование только предоставляет возможность для успешного проектирования программ. В хорошем проекте заложено решение задачи, не более сложное, чем сама задача, которую следует решить.
Составление проекта базируется на нахождении достаточно простых решений, а отнюдь не на примитивном мышлении. Обычно хорош последний вариант разработки, но никак не первый. Известным примером чрезмерного усложнения задачи является попытка описать Солнечную систему как систему, вращающуюся вокруг Земли. Две тысячи лет человечество безуспешно пыталось решить эту неверно поставленную задачу, пока не догадалось поместить Солнце в центр системы. [3]
Структурированная икра из «Светофора» за 184р Дегустирую и объясняю, что это в обще такое ❤️
Структурированные программы , полученные в прочтете доказательства теоремы о структурировании, могут быть недостаточно гюнятиымч и эффективными. [4]
Алгебра структурированных программ является мощным средством для чтения, написания и доказательства правильности структурированных программ. Она позволяет программисту путем логического преобразования справляться со сложной логикой обработки данных. Точно так же школьник методически выполняет преобразование сложных для него арифметических выражений. Алгебра дает возможность программисту представить функционирование программы в целом, а не только ход ее выполнения для конкретных данных. [5]
Разработка структурированных программ представляет собой творческий созидательный процесс, для овладения которым необходимо наличие определенных знаний и практического опыта. [6]
В структурированной программе , состоящей из некоторого числа подпрограмм, должным образом скоординированных между собой для решения поставленной задачи, на различных эгапах исполнения приходится принимать решения о том, куда следует передать управление. Единственная информация, на основе которой могут быть приняты подобные решения — это содержимое регистров, ячеек памяти и состояние условных признаков. [7]
Критическое чтение структурированной программы с целью проверки ее правильности и возможности упрощения позволяет судить о качестве ее разработки. На начальной стадии разработки структурированной программы сущность последней может быть выражена посредством мысленного анализа либо интуитивно без облечения в структурированную форму. [8]
Преобразуйте результирующую структурированную программу путем расширения новых функциональных узлов. [9]
Язык текстового описания структурированной программы ( ТОСП) предназначен для исчерпывающего описания проекта программного модуля и служит единственным документом как для составления текста программы, так и в качестве отчетного материала по этапу проектирования. [10]
Икра красная структурированная — что это такое? Пробуем и удивляемся
Таким образом, алгебра структурированных программ позволяет рассматривать структурированную программу любой сложности как составное программное выражение над меньшими структурированными программами, а любое сложное программное выражение — как одно выражение, если это, конечно, удобно. [11]
Любая простая программа функционально эквивалентна структурированной программе , составленной из элементов базисного множества последовательность, ifthenelse, whiledo с использованием функций и предикатов исходной программы, а также присваиваний и тестов над дополнительным счетчиком. [12]
Теорема правильности показывает, что все структурированные программы , выраженные через элементарные, содержащие не более одного предиката, могут быть верифицированы ( за исключением вопроса окончания программ) посредством применения методов рассуждения, требуемых для программ типа последовательность и ifthen-else. Проблемы доказательства правильности могут оказаться слишком трудоемкими, но теоретически они разрешимы. [13]
Поскольку нашей главной целью является разработка структурированных программ , возникает вопрос: какая стратегия мышления способствует вырабатыванию решений в структурированном виде. [14]
На рис. 4.18 показаны правила построения правильно структурированных программ . Правила подразумевают, что символ прямоугольника может означать в блок-схеме любое действие, включая операции ввода / вывода. [15]
Источник: www.ngpedia.ru
Алгоритмы: структурированные программы
Первоначальной целью теории алгоритмов является классификация всех задач на алгоритмически разрешимые и неразрешимые, т.е. на те, для которых существуют решающие их алгоритмы , и те, для которых таких алгоритмов нет. Неформально под алгоритмом 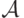 можно понимать выраженный в некотором языке набор правил (предписание, рецепт, способ), позволяющий применить к исходным (входным) данным x из некоторого множества допустимых данных X последовательность дискретных действий (операций, команд), приводящую к определенному результату — выходным данным
можно понимать выраженный в некотором языке набор правил (предписание, рецепт, способ), позволяющий применить к исходным (входным) данным x из некоторого множества допустимых данных X последовательность дискретных действий (операций, команд), приводящую к определенному результату — выходным данным 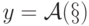 из некоторого множества Y . В этом случае говорят, что алгоритм
из некоторого множества Y . В этом случае говорят, что алгоритм 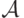 вычисляет функцию
вычисляет функцию  типа X -> Y . Это нестрогое определение вполне подходит в тех случаях, когда для некоторой функции нам предъявляется » объект «, называемый алгоритмом ее вычисления (например, алгоритм Эвклида для вычисления наибольшего общего делителя двух целых чисел), и можно легко проверить, позволяет ли он действительно вычислить требуемую функцию. Однако оно совершенно не годится для доказательства того, что для заданной функции никакого алгоритма нет.
типа X -> Y . Это нестрогое определение вполне подходит в тех случаях, когда для некоторой функции нам предъявляется » объект «, называемый алгоритмом ее вычисления (например, алгоритм Эвклида для вычисления наибольшего общего делителя двух целых чисел), и можно легко проверить, позволяет ли он действительно вычислить требуемую функцию. Однако оно совершенно не годится для доказательства того, что для заданной функции никакого алгоритма нет.
Начиная с тридцатых годов ХХ века, был предпринят ряд исследований для формализации понятия алгоритма . Перечислим некоторые из предложенных разными авторами в разное время формальных моделей: машины Тьюринга-Поста, частично-рекурсивные функции (Гедель, Клини), -исчисление (Черч, Клини), итеративные автоматы Неймана , нормальные алгорифмы Маркова, счетчиковые автоматы Минского, автоматы на графах Колмогорова-Барздиня и др. Заложенные в них идеи в значительной степени повлияли затем на архитектуру и языки программирования реальных компьютеров (например, на базе -исчисления построен широко применяемый в задачах искусственного интеллекта язык ЛИСП , а из нормальных алгорифмов Маркова произошел хорошо подходящий для текстовой обработки язык РЕФАЛ). Каждый из многочисленных языков программирования также задает некоторую формальную модель алгоритмов . Мы вначале рассмотрим один из простейших таких языков — простые структурированные программы . А затем сравним их с двумя другими моделями алгоритмов : описаниями частично рекурсивных функций и машинами Тьюринга.
Хотя алгоритмы в разных прикладных областях имеют дело с дискретными объектами различных видов: целыми и рациональными числами, строками, формулами, разного рода выражениями, графами, матрицами, таблицами, точечными изображениями и др., мы в этой части курса будем рассматривать только задачи вычисления функций от натуральных аргументов, принимающих натуральные значения. Такие функции часто называют арифметическими . Дело в том, что для любого естественного множества дискретных объектов (в частности, для всех перечисленных выше) имеется простое кодирование его элементов целыми числами. Поэтому задачи вычисления функций на этих множествах превращаются в задачи вычисления арифметических функций .
Напомним, что через N обозначается множество натуральных чисел, т.е. N= . Для частичной n — местной арифметической функции f: N n -> N через 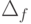 обозначим область ее определения. Чтобы указать, что f не определена на некотором наборе чисел a1. an будем писать
обозначим область ее определения. Чтобы указать, что f не определена на некотором наборе чисел a1. an будем писать  , а если f на этом наборе определена, то будем писать
, а если f на этом наборе определена, то будем писать 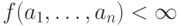 . Таким образом,
. Таким образом, 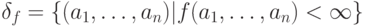 .
.
Структурированные программы
В этом разделе рассмотрим в качестве средства описания алгоритмов структурированные программы . Они вычисляют функции, используя минимальные средства: элементарные присваивания , условные операторы и циклы .
Определим вначале синтаксис структурированных программ . Зафиксируем для этого некоторое счетное множество имен переменных Var , которые будут использоваться в программах. Как обычно, будем считать, что оно включает имена x, x1,x2. , y, y1. z,z1. . и т.п. В последующих определениях x, y, z — это произвольные переменные из Var .
Определение 7.1. Оператор присваивания . Присваивание — это выражение одного из следующих трех видов:
- x := x+1
- x := 0
- x := y .
Определение 7.2. Условия. Условие — это выражение одного из двух видов:
Структурированные программы определяются индуктивно.
Определение 7.3. Структурированные программы .
- Каждое присваивание — это структурированная программа .
- Если
 и
и 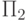 — структурированные программы , то и
— структурированные программы , то и 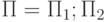 — это структурированная программа .
— это структурированная программа . - Если
 и
и 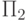 — структурированные программы , а
— структурированные программы , а  — это условие, то
— это условие, то
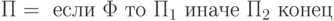
является структурированной программой .
Если  — структурированная программа , а
— структурированная программа , а  — это условие, то
— это условие, то

все является структурированной программой .
Конструкция в п. (б) называется последовательным применением или композицией программ  и
и 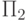 , конструкция в п. (в) называется условным оператором ; конструкция в п. (г) — это оператор цикла ,
, конструкция в п. (в) называется условным оператором ; конструкция в п. (г) — это оператор цикла ,  — условие цикла , а
— условие цикла , а  — тело цикла .
— тело цикла .
С помощью структурированных программ (далее называемых просто программами) вычисляются (частичные) функции от натуральных аргументов, принимающие натуральные значения. С каждой программой  свяжем естественным образом множество входящих в нее переменных
свяжем естественным образом множество входящих в нее переменных 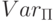 (определите это множество индукцией по построению программы). В процессе работы программа изменяет значения этих переменных . Операционная семантика задает правила такого изменения.
(определите это множество индукцией по построению программы). В процессе работы программа изменяет значения этих переменных . Операционная семантика задает правила такого изменения.
Определение 7.4. Состояние — это отображение  из множества переменных Var во множество N . Для
из множества переменных Var во множество N . Для 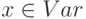 через
через 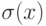 обозначим значение переменной x в состоянии
обозначим значение переменной x в состоянии 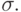 Через S обозначим множество всех состояний.
Через S обозначим множество всех состояний.
Разумеется, при рассмотрении конкретной программы  нас будут интересовать значения переменных из
нас будут интересовать значения переменных из 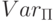 .
.
Определение 7.5. Операционная семантика программы  — это отбражение (вообще говоря, частичное) типа S -> S , которое программа
— это отбражение (вообще говоря, частичное) типа S -> S , которое программа  индуцирует на множестве всех состояний . Через
индуцирует на множестве всех состояний . Через  обозначим состояние — результат применения программы
обозначим состояние — результат применения программы  к состоянию
к состоянию  . Оно определяется индукцией по построению программы.
. Оно определяется индукцией по построению программы.
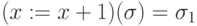 , где
, где 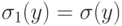 при
при 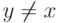 , и
, и  .
.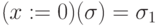 , где
, где 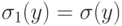 при
при 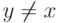 , и
, и  .
.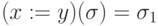 , где
, где 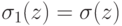 при
при  , и
, и 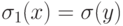
- Пусть
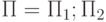 . Тогда
. Тогда 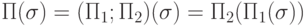 , при этом, если
, при этом, если 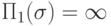 или
или 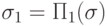 и
и  , то и
, то и 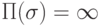 .
. - Пусть
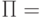 если x = y то
если x = y то иначе
иначе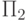 конец. Тогда
конец. Тогда
 конец. Тогда
конец. Тогда
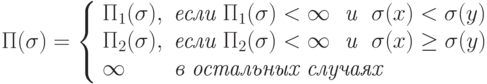
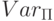 , не являющиеся входными, будем называть вспомогательными.
, не являющиеся входными, будем называть вспомогательными.
