Что такое структура данных программы

Екатерина Малахова, редактор-фрилансер, специально для блога Нетологии адаптировала статью Beau Carnes об основных типах структур данных.

«Плохие программисты думают о коде. Хорошие программисты думают о структурах данных и их взаимосвязях», — Линус Торвальдс, создатель Linux.

Структуры данных играют важную роль в процессе разработки ПО, а еще по ним часто задают вопросы на собеседованиях для разработчиков. Хорошая новость в том, что по сути они представляют собой всего лишь специальные форматы для организации и хранения данных.

В этой статье я покажу вам 10 самых распространенных структур данных. Для каждой из них приведены видео и примеры их реализации на JavaScript. Чтобы вы смогли попрактиковаться, я также добавил несколько упражнений из бета-версии новой учебной программы freeCodeCamp.

Обратите внимание, что некоторые структуры данных включают временную сложность в нотации «большого О». Это относится не ко всем из них, так как иногда временная сложность зависит от реализации. Если вы хотите узнать больше о нотации «большого О», посмотрите это видео от Briana Marie.

Топ структур данных которые должен знать программист.

В статье я привожу примеры реализации этих структур данных на JavaScript: они также пригодятся, если вы используете низкоуровневый язык вроде С. В многие высокоуровневые языки, включая JavaScript, уже встроены реализации большинства структур данных, о которых пойдет речь. Тем не менее, такие знания станут серьезным преимуществом при поиске работы и пригодятся при написании высокопроизводительного кода.

Связные списки

Связный список — одна из базовых структур данных. Ее часто сравнивают с массивом, так как многие другие структуры можно реализовать с помощью либо массива, либо связного списка. У этих двух типов есть преимущества и недостатки.

Так устроен связный список

Связный список состоит из группы узлов, которые вместе образуют последовательность. Каждый узел содержит две вещи: фактические данные, которые в нем хранятся (это могут быть данные любого типа) и указатель (или ссылку) на следующий узел в последовательности. Также существуют двусвязные списки: в них у каждого узла есть указатель и на следующий, и на предыдущий элемент в списке.

Основные операции в связном списке включают добавление, удаление и поиск элемента в списке.

Временная сложность связного списка

Упражнения от freeCodeCamp

• Work with Nodes in a Linked List
• Create a Linked List Class
• Remove Elements from a Linked List
• Search within a Linked List
• Remove Elements from a Linked List by Index
• Add Elements at a Specific Index in a Linked List
• Create a Doubly Linked List
• Reverse a Doubly Linked List

Стеки

Стек — это базовая структура данных, которая позволяет добавлять или удалять элементы только в её начале. Она похожа на стопку книг: если вы хотите взглянуть на книгу в середине стека, сперва придется убрать лежащие сверху.

Стек организован по принципу LIFO (Last In First Out, «последним пришёл — первым вышел») . Это значит, что последний элемент, который вы добавили в стек, первым выйдет из него.

Так устроен стек

В стеках можно выполнять три операции: добавление элемента (push), удаление элемента (pop) и отображение содержимого стека (pip).

Временная сложность стека

Упражнения от freeCodeCamp

• Learn how a Stack Works
• Create a Stack Class

Очереди

Эту структуру можно представить как очередь в продуктовом магазине. Первым обслуживают того, кто пришёл в самом начале — всё как в жизни.

Так устроена очередь

Очередь устроена по принципу FIFO (First In First Out, «первый пришёл — первый вышел»). Это значит, что удалить элемент можно только после того, как были убраны все ранее добавленные элементы.

Очередь позволяет выполнять две основных операции: добавлять элементы в конец очереди (enqueue) и удалять первый элемент (dequeue).

Временная сложность очереди

Упражнения от freeCodeCamp

• Create a Queue Class
• Create a Priority Queue Class
• Create a Circular Queue

Множества

Так выглядит множество

Множество хранит значения данных без определенного порядка, не повторяя их. Оно позволяет не только добавлять и удалять элементы: есть ещё несколько важных функций, которые можно применять к двум множествам сразу.

• Объединение комбинирует все элементы из двух разных множеств, превращая их в одно (без дубликатов).
• Пересечение анализирует два множества и создает еще одно из тех элементов, которые присутствуют в обоих изначальных множествах.
• Разность выводит список элементов, которые есть в одном множестве, но отсутствуют в другом.
• Подмножество выдает булево значение, которое показывает, включает ли одно множество все элементы другого множества.

Упражнения от freeCodeCamp

• Create a Set Class
• Remove from a Set
• Size of the Set
• Perform a Union on Two Sets
• Perform an Intersection on Two Sets of Data
• Perform a Difference on Two Sets of Data
• Perform a Subset Check on Two Sets of Data
• Create and Add to Sets in ES6
• Remove items from a set in ES6
• Use .has and .size on an ES6 Set
• Use Spread and Notes for ES5 Set() Integration

Map

Map — это структура, которая хранит данные в парах ключ/значение, где каждый ключ уникален. Иногда её также называют ассоциативным массивом или словарём. Map часто используют для быстрого поиска данных. Она позволяет делать следующие вещи:

• добавлять пары в коллекцию;
• удалять пары из коллекции;
• изменять существующей пары;
• искать значение, связанное с определенным ключом.

Так устроена структура map

Упражнения от freeCodeCamp

• Create a Map Data Structure
• Create an ES6 JavaScript Map

Хэш-таблицы

Так работают хэш-таблица и хэш-функция

Хэш-таблица — это похожая на Map структура, которая содержит пары ключ/значение. Она использует хэш-функцию для вычисления индекса в массиве из блоков данных, чтобы найти желаемое значение.

Обычно хэш-функция принимает строку символов в качестве вводных данных и выводит числовое значение. Для одного и того же ввода хэш-функция должна возвращать одинаковое число. Если два разных ввода хэшируются с одним и тем же итогом, возникает коллизия. Цель в том, чтобы таких случаев было как можно меньше.

Таким образом, когда вы вводите пару ключ/значение в хэш-таблицу, ключ проходит через хэш-функцию и превращается в число. В дальнейшем это число используется как фактический ключ, который соответствует определенному значению. Когда вы снова введёте тот же ключ, хэш-функция обработает его и вернет такой же числовой результат. Затем этот результат будет использован для поиска связанного значения. Такой подход заметно сокращает среднее время поиска.

Временная сложность хэш-таблицы

Упражнения от freeCodeCamp

Двоичное дерево поиска

Двоичное дерево поиска

Дерево — это структура данных, состоящая из узлов. Ей присущи следующие свойства:

1. Каждое дерево имеет корневой узел (вверху).
2. Корневой узел имеет ноль или более дочерних узлов.
3. Каждый дочерний узел имеет ноль или более дочерних узлов, и так далее.

У двоичного дерева поиска есть два дополнительных свойства:

1. Каждый узел имеет до двух дочерних узлов (потомков).
2. Каждый узел меньше своих потомков справа, а его потомки слева меньше его самого.

Двоичные деревья поиска позволяют быстро находить, добавлять и удалять элементы. Они устроены так, что время каждой операции пропорционально логарифму общего числа элементов в дереве.

Временная сложность двоичного дерева поиска

Упражнения от freeCodeCamp

• Find the Minimum and Maximum Value in a Binary Search Tree
• Add a New Element to a Binary Search Tree
• Check if an Element is Present in a Binary Search Tree
• Find the Minimum and Maximum Height of a Binary Search Tree
• Use Depth First Search in a Binary Search Tree
• Use Breadth First Search in a Binary Search Tree
• Delete a Leaf Node in a Binary Search Tree
• Delete a Node with One Child in a Binary Search Tree
• Delete a Node with Two Children in a Binary Search Tree
• Invert a Binary Tree

Префиксное дерево

Префиксное (нагруженное) дерево — это разновидность дерева поиска. Оно хранит данные в метках, каждая из которых представляет собой узел на дереве. Такие структуры часто используют, чтобы хранить слова и выполнять быстрый поиск по ним — например, для функции автозаполнения.

Так устроено префиксное дерево

Каждый узел в языковом префиксном дереве содержит одну букву слова. Чтобы составить слово, нужно следовать по ветвям дерева, проходя по одной букве за раз. Дерево начинает ветвиться, когда порядок букв отличается от других имеющихся в нем слов или когда слово заканчивается. Каждый узел содержит букву (данные) и булево значение, которое указывает, является ли он последним в слове.

Посмотрите на иллюстрацию и попробуйте составить слова. Всегда начинайте с корневого узла вверху и спускайтесь вниз. Это дерево содержит следующие слова: ball, bat, doll, do, dork, dorm, send, sense.

Упражнения от freeCodeCamp

Двоичная куча

Двоичная куча — ещё одна древовидная структура данных. В ней у каждого узла не более двух потомков. Также она является совершенным деревом: это значит, что в ней полностью заняты данными все уровни, а последний заполнен слева направо.

Так устроены минимальная и максимальная кучи

Двоичная куча может быть минимальной или максимальной. В максимальной куче ключ любого узла всегда больше ключей его потомков или равен им. В минимальной куче всё устроено наоборот: ключ любого узла меньше ключей его потомков или равен им.

Порядок уровней в двоичной куче важен, в отличие от порядка узлов на одном и том же уровне. На иллюстрации видно, что в минимальной куче на третьем уровне значения идут не по порядку: 10, 6 и 12.

Временная сложность двоичной кучи

Упражнения от freeCodeCamp

• Insert an Element into a Max Heap
• Remove an Element from a Max Heap
• Implement Heap Sort with a Min Heap

Граф

Графы — это совокупности узлов (вершин) и связей между ними (рёбер). Также их называют сетями.

По такому принципу устроены социальные сети: узлы — это люди, а рёбра — их отношения.

Графы делятся на два основных типа: ориентированные и неориентированные. У неориентированных графов рёбра между узлами не имеют какого-либо направления, тогда как у рёбер в ориентированных графах оно есть.

Чаще всего граф изображают в каком-либо из двух видов: это может быть список смежности или матрица смежности.

Граф в виде матрицы смежности

Список смежности можно представить как перечень элементов, где слева находится один узел, а справа — все остальные узлы, с которыми он соединяется.

Матрица смежности — это сетка с числами, где каждый ряд или колонка соответствуют отдельному узлу в графе. На пересечении ряда и колонки находится число, которое указывает на наличие связи. Нули означают, что она отсутствует; единицы — что связь есть. Чтобы обозначить вес каждой связи, используют числа больше единицы.

Существуют специальные алгоритмы для просмотра рёбер и вершин в графах — так называемые алгоритмы обхода. К их основным типам относят поиск в ширину (breadth-first search) и в глубину (depth-first search). Как вариант, с их помощью можно определить, насколько близко к корневому узлу находятся те или иные вершины графа. В видео ниже показано, как на JavaScript выполнить поиск в ширину.

Временная сложность списка смежности (графа)

Упражнения от freeCodeCamp

• Introduction to Graphs
• Adjacency List
• Adjacency Matrix
• Incidence Matrix
• Breadth-First Search
• Depth-First Search

Узнать больше

Если до этого вы никогда не сталкивались с алгоритмами или структурами данных, и у вас нет какой-либо подготовки в области ИТ, лучше всего подойдет книга Grokking Algorithms. В ней материал подан доступно и с забавными иллюстрациями (их автор — ведущий разработчик в Etsy), в том числе и по некоторым структурам данных, которые мы рассмотрели в этой статье.

Мнение автора и редакции может не совпадать. Хотите написать колонку для «Нетологии»? Читайте наши условия публикации.

Средняя оценка 5 / 5. Всего проголосовало 1

Источник: netology.ru

Что такое структура данных программы

Комментарии

Популярные По порядку
Не удалось загрузить комментарии.

ЛУЧШИЕ СТАТЬИ ПО ТЕМЕ

10 структур данных, которые вы должны знать (+видео и задания)

Бо Карнс – разработчик и преподаватель расскажет о наиболее часто используемых и общих структурах данных. Специально для вас мы перевели его статью.

Какие алгоритмы нужно знать, чтобы стать хорошим программистом?

Данная статья содержит не только самые распространенные алгоритмы и структуры данных, но и более сложные вещи, о которых вы могли не знать. Читаем и узнаем!

Изучаем алгоритмы: полезные книги, веб-сайты, онлайн-курсы и видеоматериалы

В этой подборке представлен список книг, веб-сайтов и онлайн-курсов, дающих понимание как простых, так и продвинутых алгоритмов.

Источник: proglib.io

Структуры данных, которые необходимо знать каждому программисту

Пройти путь от нуля до профессионального инженера-программиста можно исключительно с помощью бесплатных ресурсов в интернете. Но разработчики, которые идут по этому пути, часто игнорируют концепцию структур данных. Они считают, что эти знания не принесут им пользы, поскольку они будут разрабатывать только простые приложения.

Однако уделять внимание структурам данных важно с самого начала обучения, так как они повышают эффективность приложений. Хотя это не означает, что нужно везде применять эти структуры — не менее важно понимать, когда они будут лишними.

Что такое структура данных?

Независимо от профессии, ежедневная работа связана с данными. Шеф-повар, инженер-программист или даже рыбак — все они работают с теми или иными формами данных.

Структуры данных — это контейнеры, которые хранят данные в определенном формате. Этот специфический формат придает структуре данных определенные качества, которые отличают ее от других структур и делают ее пригодной (или напротив, неподходящей) для тех или иных сценариев использования.

Рассмотрим некоторые из наиболее важных структур данных, которые помогут создавать эффективные решения.

Массивы

Массивы — одна из самых простых и часто применяемых структур данных. Такие структуры данных, как очереди и стеки, основаны на массивах и связанных списках (которые мы рассмотрим чуть позже).

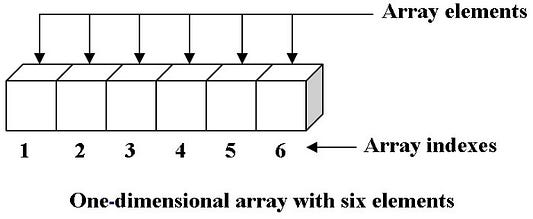
Каждому элементу в массиве присваивается положительное целое число, которое обозначает положение элемента. Это число называется индексом. В большинстве языков программирования индексы начинаются с нуля. Эта концепция называется нумерацией на основе нуля.

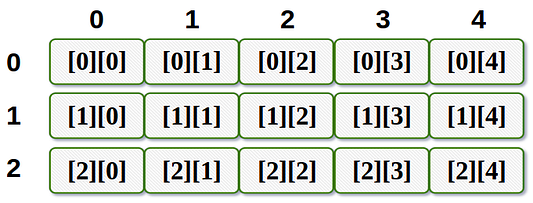
Существует два типа массивов: одномерные и многомерные. Первые представляют собой простейшие линейные структуры, а вторые — вложенные и включают другие массивы.

Основные операции с массивами

• Get — получить элемент массива по заданному индексу.
• Insert — вставить элемент массива по заданному индексу.
• Length — получить количество элементов в заданном массиве.
• Delete — удалить элемент массива по заданному индексу. Может быть выполнено либо путем установки значения undefined , либо путем копирования элементов массива, за исключением удаляемого, в новый массив.
• Update — обновление значения элемента массива по заданному индексу.
• Traverse — проход цикла через массив для выполнения функций над элементами массива.
• Search — поиск определенного элемента в заданном массиве с помощью выбранного алгоритма.

Применение массивов

• Представляют собой строительные блоки более сложных структур данных, таких как стеки, очереди и т.д.
• Подходят для хранения несложных связанных данных благодаря простоте использования.
• Используются для различных алгоритмов сортировки, таких как сортировка вставок, сортировка пузырьком и т.д.

Связанный список (Linked List)

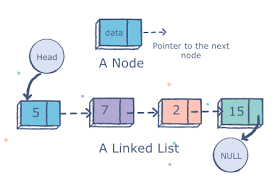
Связанный список — это набор элементов, называемых узлами, в линейной последовательной структуре. Узел — простой объект с двумя свойствами. Это переменные для хранения данных и адреса памяти следующего узла в списке. Поэтому узел знает только о том, какие данные он содержит и кто его сосед. Это позволяет создавать связанные списки, в которых каждый узел связан с другим.

Существует несколько типов связанных списков.

• Односвязный. Обход элементов может выполняться только в прямом направлении.
• Двусвязный. Обход элементов может выполняться как в прямом, так и в обратном направлениях. Узлы включают дополнительный указатель, известный как prev , указывающий на предыдущий узел.
• Круговые связанные. Это связанные списки, в которых предыдущий ( prev ) указатель “головы” указывает на “хвост”, а следующий указатель “хвоста” указывает на “голову”.

Основные операции со связанными списками

• Insertion — добавление узла в список. Это может быть сделано на основе требуемого местоположения, такого как голова, хвост или где-то посередине.
• Delete — удаление узла в начале списка или на основе заданного ключа.
• Display — отображение полного списка.
• Search — поиск узла в данном связанном списке.
• Update — обновление значения узла в заданном ключе.

Применение связанных списков

• В качестве строительных блоков сложных структур данных, таких как очереди, стеки и некоторые типы графиков.
• В слайд-шоу изображений, поскольку изображения идут строго друг за другом.
• В динамических структурах для выделения памяти.
• В операционных системах для легкого переключения вкладок.

Стек

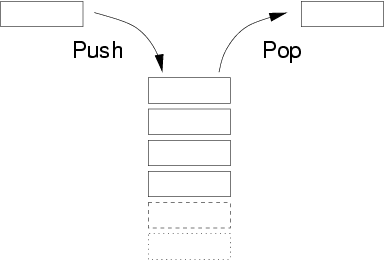
Стек — линейная структура данных, которая создается на основе массивов или связанных списков. Стек следует принципу Last-In-First-Out (LIFO, “первым на вход — последним на выход”), т.е. последний элемент, вошедший в стек, будет первым, кто покинет его. Причина, по которой эта структура называется стеком, в том, что ее можно визуализировать как стопку книг на столе (по-английски stack).

Основные операции со стеком

• Push — вставка элемента в верхнюю часть стека.
• Pop — удаление элемента из верхней части стека с возвращением элемента.
• Peek — просмотр элемента в верхней части стека.
• isEmpty — проверка пустоты стека.

Применение стеков

• В истории навигации браузера.
• Для реализации рекурсии.
• При выделении памяти на основе стека.

Очередь

Как и стек, очередь — это еще один тип линейной структуры данных, основанной либо на массивах, либо на связанных списках. Очереди отличаются от стеков тем, что они основаны на принципе First-In-First-Out (FIFO, “первым на вход — первым на выход”), где элемент, который входит в очередь первым, и покинет ее первым.

Реальная аналогия структуры данных “очереди” — это очередь людей, ожидающих покупки билета в кино.

Основные операции с очередями

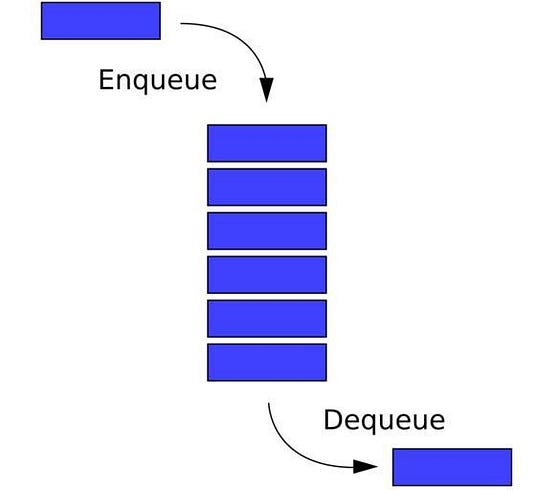
• Enqueue — вставка элемента в конец очереди.
• Dequeue — удаление элемента из передней части очереди.
• Top/Peek — возвращает элемент из передней части очереди без удаления.
• isEmpty — проверка содержимого очереди.

Применение очередей

• Обслуживание нескольких запросов на одном общем ресурсе.
• Управление потоками в многопоточных средах.
• Балансировка нагрузки.

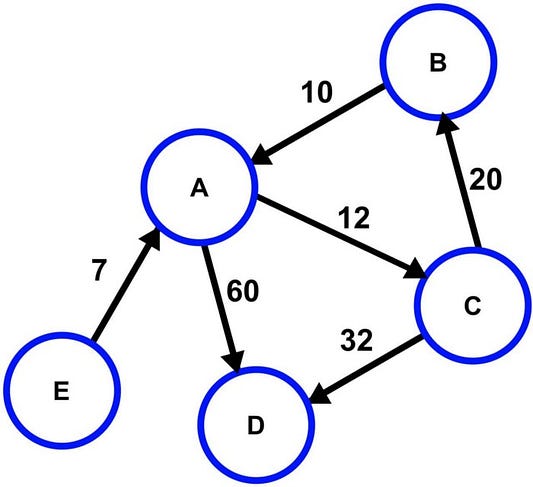
Граф

Граф — это структура данных, представляющая собой взаимосвязь узлов, которые также называются вершинами. Пара (x,y) называется ребром. Это указывает на то, что вершина x соединена с вершиной y . Ребро может указывать на вес/стоимость, то есть стоимость прохождения по пути между двумя вершинами.

Ключевые термины

• Размер — количество ребер в графике.
• Порядок — количество вершин в графе.
• Смежность — случай, когда два узла соединены одним и тем же ребром.
• Петля — вершина, соединенная ребром сама с собой.
• Изолированная вершина — вершина, которая не связана с другими вершинами.

Графы делятся на два типа. Они различаются главным образом по направлениям пути между двумя вершинами.

• Ориентированные графы: все ребра имеют направления, указывающие начальную и конечную точки (вершины).
• Неориентированные графы: ребра не имеют направлений, которые позволяют обходам происходить с любого направления.

Распространенные алгоритмы обхода графов

• Поиск в ширину (BFS) — метод поиска кратчайшего пути в графе, основанный на вершинах.
• Поиск в глубину (DFS) — метод, основанный на ребрах.

Основные операции с графами

• Add vertex : добавить вершину в граф.
• Add edge : добавить ребро между двумя вершинами.
• Display : отобразить вершину.
• Total cost of traversal : найти общую стоимость пути обхода.

Применение графов

• Для представления потоковых вычислений.
• При распределении ресурсов операционной системой.
• Реализация алгоритмов поиска друзей в Facebook.
• Расчет кратчайшего пути между двумя локациями (Google Maps).

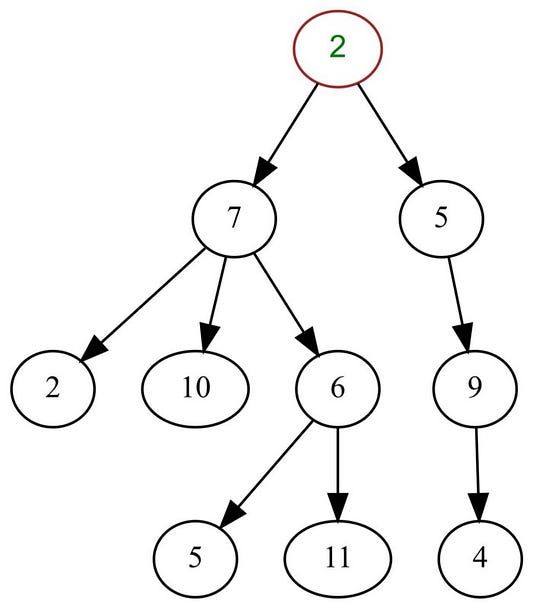
Дерево

Дерево — это иерархическая структура данных, состоящая из вершин (узлов) и ребер, которые их соединяют. Деревья часто используются в системах искусственного интеллекта и сложных алгоритмах, поскольку обеспечивают эффективный подход к решению проблем. Дерево — это особый тип графа, который не содержит циклов. Некоторые утверждают, что деревья полностью отличаются от графов, но эти аргументы субъективны.

Существует несколько типов деревьев.

• N-арное дерево.
• Сбалансированное дерево.
• Бинарное дерево.
• Бинарное дерево поиска (BST).
• Дерево AVL.
• Красно-черное дерево.
• 2-3-дерево.

BST — самые распространенные типы деревьев.

Основные операции с BST

• Insert — вставка элемента в дерево.
• Search — поиск элемента в дереве.
• PreorderTraversal — обход дерева прямым способом.
• InorderTraversal — обход дерева центрированным способом.
• PostorderTraversal — обход дерева обратным способом.

Применение деревьев

• Представление организации.
• Представление компьютерной файловой системы.
• Представление химической формулы.
• В деревьях принятия решений.
• Внутри JVM (Java Virtual Machine) для хранения объектов Java.

Хэш-таблица

Хэш-таблица хранит данные в парах ключ-значение. Это означает, что каждый ключ в хэш-таблице имеет некое значение, связанное с ним. Такая простая компоновка обеспечивает эффективность хэш-таблиц, независимо от их размера, при работе с данными.

Хэш-таблицы похожи на обычное хранилище данных с парой ключ-значение, однако их отличает способ генерации ключей. Они создаются с помощью специального процесса, называемого хэшированием.

Хеширование (хэш-функция)

Хэширование — это процесс, который с помощью хэш-функции преобразует ключ для получения хэшированного ключа. Эта хэш-функция определяет индекс таблицы или структуры, в которых должно храниться значение.

h(k) = k % m

• h — хэш-функция.
• k — ключ, из которого должно быть определено хэш-значение.
• m — размер хэш-таблицы.

Например, рассмотрим использование хэш-функции k%17 . Если исходный ключ равен 20 , то хэшированный будет 20%17=3 . Значение будет храниться в хэш-таблице под индексом 3 .

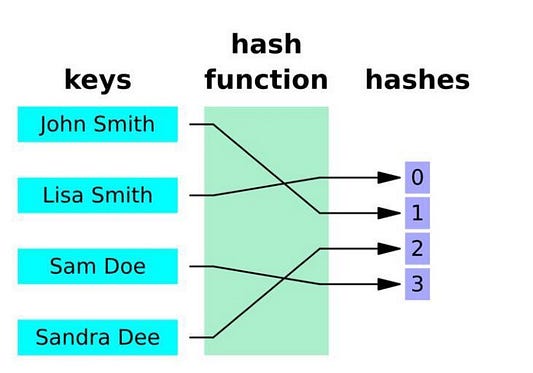
Зачем нужен хэш?

Некоторые задаются вопросом, зачем проходить через дополнительный процесс хэширования, когда можно просто сопоставить значения непосредственно с ключом. Хотя прямое сопоставление несложно, оно может оказаться неэффективным при работе с большим набором данных. С помощью хеширования можно достичь почти постоянного времени O(1).

Коллизии

Поскольку для преобразования ключей используется общая хэш-функция, существует вероятность коллизий. Рассмотрим приведенный ниже пример с учетом хэш-функции k%17 .

• Когда k = 18, h(18) = 18%17 = 1.
• При k = 20, h(20) = 20%17 = 3.
• При k = 35, h(35) = 35%17 = 1.

Когда ключи равняются 18 и 35, происходит коллизия, поскольку они направляются к индексу 1.

Коллизии можно разрешить с помощью таких стратегий, как раздельная цепочка и открытая адресация.

Основные операции с хэш-таблицами

• Search — поиск элемента в хэш-таблице.
• Insert — вставка элемента в хэш-таблицу.
• Delete — удаление элемента из хэш-таблицы.

Применение хэш -таблиц

• В индексации баз данных.
• При проверке орфографии.
• При реализации заданной структуры данных.
• В кэше.

Разработчикам важно знать хотя бы основы этих структур, поскольку при правильной реализации они помогут повысить эффективность ваших приложений.

Спасибо за чтение!

• Пять отличных Python-библиотек для data science
• 4 пайтонические техники для краткого кода
• 10 актуальных профессий в области науки о данных

Источник: nuancesprog.ru