Что такое система счисления это компьютерная программа для арифметических вычислений

Система счисления — это совокупность цифровых знаков и правил их записи, применяемая для однозначной записи чисел. Все системы счисления подразделяются на позиционные и непозиционные.

Непозиционной называется такая система счисления, в которой значение цифры не зависит от ее положения в ряду цифр, изображающих число. Древние египтяне применяли систему счисления, состоящую из набора символов, изображавших распространенные предметы быта. Совокупность этих символов представляла число. Расположение символов в числе не имело значения, отсюда и появилось название – непозиционная система счисления. Примером является римская система счисления, в которой для обозначения отдельных чисел используются буквы римского алфавита. Цифры в римской системе обозначаются различными знаками:

1 — I; 3 — III; 5 — V; 10 — X; 50 — L; 100 — С; 500 — D; 1000 — М. Запись числа осуществляется по каждый меньший знак, поставленный справа, он прибавляется к его значению, а слева — вычитается из него: так, ХС — 90; СХ — 110; MCMLXXXVIII — 1988. Выполнять арифметические действия в непозиционных системах неудобно. Поэтому в настоящее время эти системы не используются для расчетов.

СИСТЕМЫ СЧИСЛЕНИЯ С НУЛЯ | ОСНОВЫ ПРОГРАММИРОВАНИЯ

Позиционной называется такая система счисления, в которой значение цифры зависит от ее положения в ряду цифр (позиции), изображающих число.

Первая известная нам позиционная система счисления – шестидесятеричная вавилонская система счисления. Следы этой системы счисления сохранились и сегодня в способах измерения и записи величин углов и времени.

Сегодня мы пользуемся индо-арабской системой счисления, где имеется десять цифр: от 0 до 9. Эта система счисления получила название десятичной.

Позиционная система счисления (ПСС) характеризуется количеством различных цифр, используемых для записи чисел. Максимальное количество различных цифр, используемых для записи чисел в данной системе счисления, называется основанием системы счисления. Основание системы счисления определяет ее название.

В позиционной системе счисления каждый разряд имеет вес. Весом разряда называется число b n , где b – основание системы счисления, а n – номер разряда. Например, в десятичном числе 1276 цифра 2 имеет значение 200, т.к. вес разряда, в котором записана эта цифра, равен 100, т.е. 10 2 = 100.

Любое число, записанное в ПСС с основанием p, может быть представлено в следующем виде:

(2.1)

где — любая цифра (символ), используемая в данной ПСС из множества р — 1>; n, … , m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме

и ; — веса разрядов. Например, число = 1235,87 по (2.1) имеет вид:

СИСТЕМЫ СЧИСЛЕНИЯ для новичков

В ЭВМ применяют ПСС с основанием 2 — двоичную. Поскольку число, записанное в двоичной системе счисления очень громоздкое, то для удобства работы применяют восьмеричную и шестнадцатеричную системы счисления. В таблице 2.1 показано соответствие записи чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления.

Соответствие записи чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления

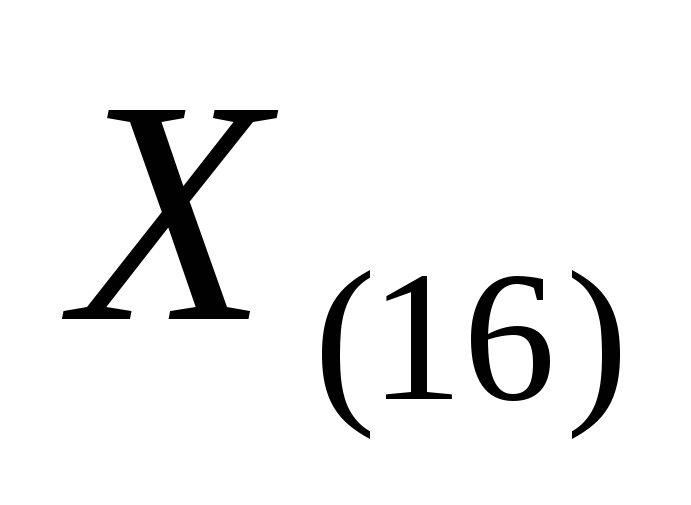
Двоичная ПСС получила самое широкое применение в ЭВМ благодаря следующим достоинствам. Удобства кодирования информации и простота выполнения арифметических операций.

Т.к. одно из необходимых условий работы компьютера – наличие напряжения, вся информация в компьютере представлена с помощью напряжений, т.е. закодирована какими то напряжениями. Для удобства кодировки полагают, что если напряжение есть, то это состояние обозначают 1, если нет, то 0. Эти цифры называются двоичными (от английского binary digit). Сокращение этого выражения привело к появлению термина bit, ставшего названием разряда двоичного числа. Итак, две цифры 0 и 1 есть, а как записать другие цифры в компьютере. Для этого используется код числа – т.е. комбинация 0 и 1. Как оказалось, реализация элементов, которые должны различать одно из двух состояний (0 или 1) и их комбинаций, оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.

Для кодирования символьной информации используются кодовые таблицы. Сегодня самая распространенная кодовая таблица – это ASCII – (American Standard Cord for Information Interchange) американский стандарт. В системе ASCII закреплены две таблицы кодирования – базовая и расширенная. Базовая таблица закрепляет значение кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.

Первые 32 кода базовой таблицы отданы производителям аппаратных средств (в первую очередь производителям компьютеров и печатающих устройств). В этой области размещаются так называемые управляющие коды, которым не соответствуют никакие символы языков, и эти коды не выводятся ни на экран, ни на устройства печати, но ими можно управлять тем, как производится вывод прочих данных.

Начиная с кода 32 по код 127 размещены коды символов английского алфавита, знаков препинания, цифр, арифметических действий и некоторых вспомогательных символов. Принцип построения кодовых таблиц следующий. Количество всех символов (английские и русские большие и малые буквы, цифры, знаки препинания и т.п.) менее 255.

Максимальное число, которое можно записать в 1 байт – это 8 единичек = 255. Поэтому используя 1 байт можно закодировать все символы. Таблицу строят следующим образом: по горизонтали и по вертикали записывают числа от 0 до 15. Получим таблицу 16 строк на 16 столбцов, т.е. 256 клеточек.

В каждую клетку записывают какой-то символ. Код символа получают записав в шестнадцатеричной системе счисления число, которое состоит из номера столбца и номера строки. Например,

Источник: studfile.net

Cистемы счисления — история, виды, отличия

Со школы люди хорошо знакомы с римскими и арабскими цифрами и привыкли к обозначению чисел с их помощью. Однако такие системы счета образовались не сразу, и мало кто знает, что они были не единственными в истории человечества. С появлением электроники, системы счисления и вовсе преобразовались; подстроились под нужны людей, раскрыв многогранность подходов к применению чисел.

Немного истории

Необходимость обозначать количество цифрами появилось не сразу. На первых этапах развития общества люди еще не пользовались понятием «число» , но могли определить совокупность двух-трех предметов, считая за «много» все, что больше. Кроме того, использовались различные предметы для сопоставления количества подсчитываемых предметов и специальных знаков — зарубок на ветке, камешков в чаше, узлов на веревке.

Сравнительно позже люди поняли, что такой способ счета неудобен, когда речь касается большого количества предметов . Так люди пришли к необходимости обозначать одним знаком или их сочетанием сразу много вещей, то есть к четкому определению цифр, чисел и системе счисления.

Что такое система счисления?

Система счисления — это знаковая система, состоящая из символов и правил для обозначения чисел. Знаки при этом называют цифрами, а их совокупность — алфавитом .

Любая система счисления основана на обозначении узловых чисел . А остальные числа, которые можно составить из узловых, называют алгоритмическими . Их получают в ходе операций сложения либо вычитания.

Например, в римской системе узловыми считаются числа 1, 5, 10, 50, 100, 500 и 1000. И, чтобы составить алгоритмическое число 121, необходимо вспомнить правила записи римских чисел. Так, чтобы получить 121, требуется составить следующее выражение:

100 + 10 + 10 + 1 = M + X + X +I = MXXI

Виды систем счисления

1. Унарная. Это самая простая система счисления, так как ее алфавит состоит всего из одного символа — единицы. Поэтому она и называется унарной или единичной. В Древние времена именно ее использовали люди при отображении количества предметов палочками, камушками и зарубками. Длина записи числа при этом была напрямую связана с его величиной.
2. Непозиционные. Непозиционные системы счисления основаны на том, что условный вес цифры не связан с ее положением в записи числа. Примерами таких систем являются древнегреческая, древнеримская и древнеегипетская. В них значение разряда может состоять из нескольких цифр, которые, стоящие в разных местах, имеют разный вес для числа в целом.
3. Позиционные. Для данных систем значение числа тесно связано с положением цифры в нем. Например, в десятичной число можно поделить на разряды. И в зависимости от разряда, которому принадлежит цифра, определяется величина числа.
4. Смешанные. Смешанные счисления могут определяться алфавитом одной системы, а правилом построения чисел — другой. Такой способ передачи чисел используют в ЭВМ, когда компьютеру необходимо перевести числа с двоичного кода в десятичный, которой пользуются люди в обычной жизни.

Чем позиционная система отличается от непозиционной?

Если рассмотреть одно и то же число в двух этих системах, то можно увидеть, как меняется его вес в зависимости от места цифры в его записи.

Например, цифры 1 и 5 в десятичной системе счисления для римской будут иметь следующий вид: I и V. Но записав их в одном и том же порядке мы получим различные числа для разных видов счисления:

15=10+5
IV=V-I=4
51=50+1
VI=V+I=6

Соответственно, для непозиционной системы счисления положение цифры в записи не имеет значения, а учитываются только правила построения чисел.

Системы счисления в информатике

В информатике принято выделять четыре основных системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Связано это, в первую очередь, с их использованием в различных отраслях программирования.

Так, восьмеричная система требуется для перевода в двоичные числа на цифровых устройствах и в компьютерной документации. Позднее ей на смену пришла шестнадцатеричная, которую используют для записи символов Юникода. Однако восьмеричный код до сих пор применяется в системе Linux. Наиболее же распространенной системой является двоичная, которая используется в программировании практически всех ЭВМ.

Смотрите также:

• Смотрите также
• Калькуляторы
• Популярные переводы

Полезные материалы

• Что такое позиционная система счисления?
• Что такое непозиционная система счисления?
• Двоичная система счисления — что это такое?
• Как из десятичной системы счисления перевести в двоичную?
• Как из двоичной системы счисления перевести в десятичную?

Источник: sistemy-schisleniya.ru

Все о системах счисления в информатике

Когда речь заходит об IT и информатике, пользователям и разработчикам приходится иметь дело с разнообразными системами счисления. Они помогают отображать данные, а также вести запись чисел и символов на устройстве.

В данной статье будет рассказано о том, какие системы счисления существуют, для чего они необходимы, где применяются. Соответствующие темы обычно затрагиваются еще в школах – на уроках информатики в средних-старших классах. Поэтому каждый уважающий себя разработчик должен хорошо разбираться в обозначенном направлении.

Определение

Система счисления (СС) – это специальная система записи для выражения чисел. Математическое представление чисел заданного набора с использованием цифр и иных символов согласованным образом.

Совокупность правил записи чисел через символьно-цифирные конечные наборы. Одна и та же последовательность может быть представлена разными числами в различных системах «записи». Пример – 11 в десятичной системе, три – в двоичной, два – в унарной.

Значения и их особенности

Значение – это число, которое представляет та или иная цифра. Не все рассматриваемые компоненты могут работать со всеми числами, используемыми сегодня. Примеры – римские «значения». У них нет нуля.

• представляет полезный набор чисел (примеры – целые, рациональные);
• дает уникальное представление каждому имеющемуся элементу;
• отражает алгебраические или арифметические структуры.

Без систем невозможна работа с компьютерами. Именно поэтому соответствующее направление требует отдельного внимания.

Виды

Существуют различные виды СС:

1. Непозиционные. В них значение не зависит от ее позиции.
2. Позиционные. «Итог» зависит от того, где именно стоит тот или иной компонент.
3. Однородные.
4. Неоднородные.

Каждый вариант предусматривает свои ключевые особенности.

Позиционный тип

Здесь значение каждой цифры будет зависеть от ее разряда в числе. Пример – для человека привычна 10-я СС. Она является позиционной. 453 рассмотрено в виде примера. Тут 4 – это сотни, что указывает на 400, 5 – десятки (50), 3 – единицы (3).

Чем больше разряд, тем выше окажется значение.

Непозиционный тип

Самый древний вариант. Каждый компонент – это отдельная величина. Она никак не зависит от разряда. В программировании не используется, поэтому рассматривать его более подробно не рекомендуется.

Однородный тип

Однородный вариант – это тот, в котором для всех позиций числа набор допустимых символов будет одинаковым. Пример – десятичная система. Для записи элемента можно использовать в каждом разряде только одну цифру. А именно – от 0 до 9. Запись 450 допускается (1-й разряд – 0, 2 – 5, 3-й – 4), а вот 4F5 – нет.

Смешанный тип

В нем в каждом разряде допускается разный набор других позиций. Пример – это измерение времени:

• в секундах – 60 символов;
• в часах – 24;
• в сутках – 365.

Теперь можно рассмотреть, какие СС встречаются в информатике чаще всего.

Десятичная СС

Самая распространенная. Это – часть позиционной системы счисления. Применяется в обыденной жизни повсеместно. Каждый разряд здесь – это только одна цифра. Диапазон составляет от 0 до 1 включительно.

Основание системы счисления – 10.

Чтобы лучше понять принцип использования, стоит рассмотреть пример – 503. В непозиционной СС оно выглядело бы так: 5 + 0 + 3 = 8. В позиционной каждая цифра числа умножается на основание, возведенное в степень, равную номеру разряда.

Чтобы избежать путаницы, запись будет выглядеть так: 503=50310. Используется нижний индекс.

Двоичная

Двоичную систему счисления в основном используют устройства и компьютеры. Такое решение пришло из-за того, что 10-я СС требовала раньше огромных затрат. Это сказывалось на стоимости ЭВМ.

Пришлось создавать «урезанную» версию. Основание здесь – 2. Для записи используются символы:

Каждый разряд имеет только одно соответствующее значение. Пример 101. Это – десятичное 5. Для того, чтобы осуществить перевод из двоичной СС в 10-ю, требуется умножить цифру 2-го числа на 2. Возвести «двойку» в степень, равную разряду. Так 1012 будет:

Для работы с кодами ЭВМ хранит для каждой отдельной цифры триггер. Это – электронная схема, принимающая два состояния. Одно – соответствует «нулю», другое – «единице».

Для того, чтобы запомнить отдельное число, применяется регистр – группа триггеров, количество которых соответствует количество разрядов в двоичном числе. А их совокупность – это оперативная память. Число, которое содержится в регистре, носит название машинного слова. Для получения доступа их нумеруют. Номер – адрес ячейки.

Восьмеричная СС

Восьмеричная система применяется в технике и гаджетах. В качестве основания выступает 8. Содержит для записи цифры в диапазоне от 0 до 7.

Пример – 254. Для того, чтобы перевести его в 10-ю СС, нужно каждый разряд исходного «компонента» умножить на 8n, где n – это количественный номер разряда. Получится: 2*8 2 + 5*8 1 + 4*8 0 = 128+40+4=17210.

Шестнадцатеричная система

Шестнадцатеричную систему счисления используют в современных компьютерах достаточно часто. Пример – с ее помощью можно задать цвет.

Она имеет основание 16. Для выражения чисел система использует числа 0-9, а также буквы A-F. Буквенные записи соответственно будут равны 10, 11, 12, 13, 14 и 15.

Чтобы лучше понимать принцип «работы» этой СС, стоит рассмотреть наглядный пример – 4F1516. Чтобы перевести его в 8-ю, нужно:

1. Преобразовать число в двоичное.
2. Разбить на группы по 3 разряда (элемента).

Для перевода в 2-е число каждая цифра представлена в виде 4- разрядного числа:

В первой и последней группах не хватает разряда. Они дополняются нулями: 0100 1111 0101. Это значение разделяется на группы по 3 компонента справа-налево. Получается 010 011 110 101.

Для того, чтобы увидеть результат, нужно перевести каждую двоичную группу в восьмеричную систему. Разряды умножаются на 2 n , где n – это номер того или иного разряда. На выходе получится 23688.

Восьмеричную и шестнадцатеричную системы счисления активно изучают в школах на уроке информатики. Они не слишком нужны среднестатистическим пользователям, но пригодятся тем, кто планирует углубляться в программирование.

О преобразованиях

Работая с любой систе мой счисления, нужно понимать, как переводить число из одного «варианта» в другой. Эти навыки пригодятся каждому, кто планирует углубляться в IT.

В десятичную

Первый вариант – это любую «систему» привести к «десятичному виду». Тому, что привычен каждому пользователю.

Пусть будет дано число a1a2a3, где основание – это b. Тогда нужно каждый разряд умножить на b n . N выступит номером разряда. Формула перевода окажется: (a1a2a3)b=(a1*b 2 +a2*b 1 +a3*b 0 )10.

Из десятичной

Из десятичной системы счисления можно преобразовать число в любую другую. Здесь стоит разделить процесс на формирование дробной и целой частей. Иначе добиться желаемого результата не получится.

В случае с целой частью действовать необходимо так:

1. Последовательно выполняется деление целой части на основание новой системы. Делается это до тех пор, пока число не станет нулем.
2. Полученные остатки – это цифры искомого компонента.
3. Запись осуществляется с последнего остатка до первого.

Дробная часть преобразуется так:

1. Соответствующий элемент умножается на основание системы, в которую осуществляется перевод.
2. Целая часть отделяется.
3. Умножить дробную часть на основание новой. Делать это до тех пор, пока она не будет равна 0.
4. Записать полученный результат умножения. Делается это в порядке, соответствующем получению.

Пример – 1510 при переводе в восьмеричную систему счисления – это 178. Получилось как: 15/8 = 1, остаток – 7, а также 1/8 = 0, остаток 1.

Из двоичной в восьмеричную и шестнадцатеричную

Для того, чтобы перевести 1 a (число) из двоичной в 8-ю систему, нужно:

1. Разбить его на группы по 3 компонента справа-налево.
2. Недостающие разряды дополнить ведущими нулями.
3. Преобразовать каждую группу при помощи умножения разряда на 2 n .

Аналогично действовать нужно с шестнадцатеричной системой, но делить компонент необходимо на группы по 4 элемента.

Из 8-ой и 16-ой в 2-ю

В случае с восьмеричной системой – каждый разряд числа преобразуется в 3-х разрядное двоичное путем деления на 2. Недостающие крайние разряды – это нули.

Шестнадцатеричная система предусматривает преобразование каждого разряда в двоичное 4-х компонентное. Сопровождается делением на 2. Недостающие крайние разряды – это нули.

Быстрое погружение в основы

Чтобы научиться работать в непозиционной системе счисления или любой другой, стоит углубиться в основы информатики. В этом помогут специализированные дистанционные онлайн курсы.

На них пользователя с нуля обучат основам информатики, программирования, дизайна и графики. Помогут освоить в кратчайшие сроки инновационные IT-профессии. В конце каждого курса пользователи получают официальные электронные сертификаты.

Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Источник: otus.ru

Информатика — система счисления. Виды систем счисления

В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.

Что это значит?

Начнем с определения основного понятия. Как отмечает учебник «Информатика», система счисления — это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.

В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.

В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.

В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.

Непозиционные системы

К непозиционным системам счисления относятся:

1. Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
2. Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.
3. Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
4. Вавилонская система счисления, в которой использовалось всего два обозначения для записи – клинья и стрелочки.
5. В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.

Позиционные системы

Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:

• двоичная;
• восьмеричная;
• десятичная;
• шестнадцатеричная;
• шестидесятеричная, используемая при счете времени (к примеру, в минуте — 60 секунд, в часе — 60 минут).

Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.

Десятичная система

Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.

Двоичная система

Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.

Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.

Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Восьмеричная система

Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.

Двоично-десятичная система

Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах.

В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.

Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.

Шестнадцатеричная система

В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.

При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.

Перевод чисел: из десятичной в двоичную

Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.

Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.

Например, переведем число 9 в двоичную систему:

Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.

После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.

Проводим ту же операцию с 2. В остатке получаем 0.

В итоге деления у нас получается 1.

Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.

Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.

Перевод чисел: из двоичной в десятичную

Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.

Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.

Для школьников этот алгоритм можно объяснить проще:

Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.

Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.

Выглядеть это будет следующим образом:

1*2 3 + 0*2 2 +0*2 1 +1*2 0 = 8+0+0+1 =9.

При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.

Другие варианты перевода

В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».

Арифметические операции

Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.

Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.

Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.

Источник: fb.ru