Современный мир беспрестанно развивается. Раньше многие понятия были сокрыты от людей, считались непонятными. Так появилось программирование с собственными алгоритмами. Специально обученные люди пользуются некими «машинными языками», чтобы создавать программы и игры, «общаться» с компьютерами и другими устройствами.
Но некоторые термины у программеров появились, благодаря точным наукам – физике, математике и так далее. Существуют так называемые рекурсивные алгоритмы, без которых продвинутому разработчику/программисту придется туго. В данной статье будет рассказано о том, что соответствующий термин значит, как используется на практике в «машинном языке».
Программирование – определение
Но перед определением упомянутого термина требуется разобраться с другими важными понятиями. Что такое программирование, о котором тоже зайдет речь, понимает далеко не каждый.
Так описывают процедуру создания компьютерных программ, игр, приложений. Основывается на применении определенного синтаксиса. А именно – языка программирования.
Рекурсия / Введение в программирование, урок 8 (JavaScript ES6)
Сейчас есть программирование как на мобильных, так и на компьютерных платформах. Люди, занимающиеся написанием кодов программ, называются программистами.
Язык программирования
Язык программирования – некий сборник формальных правил, согласно которым пишутся всевозможные программы. Требуется для того, чтобы пользователь/программер мог «общаться» с компьютерами и другими устройствами.
Языков существует огромное множество. Каждый обладает собственным синтаксисом, функциями, операторами, посредством которых составляются выражения. Условно разделяются на:
- объектно-ориентированные;
- декларативные.
Первые просты в освоении, так как используют в процессе создания приложения независимые объекты и их группы. Декларативные языки предусматривает установление связи между информационными первоначальными структурами, а также конечным результатом.
Рекурсивные функции присутствуют в каждом языке. Если разобраться с ними, получится быстро производить различные расчеты через компьютеры, а также составлять расчетные приложения.
Рекурсия – что это такое
Рекурсией называется некое свойство объекта или вещи, позволяющее заниматься подражанием самому себе. Предмет рекурсивный, если его части обладают такой же «внешностью», как и весь он целиком. Имеет широкое распространение в математике, физике, написании машинных кодов.
В случае с компьютерами упомянутым свойством обладают преимущественно функции. Они также зовутся методами.
Рекурсией при подобных обстоятельствах называют способ определения функций, при котором результат возврата для соответствующего аргумента определится на основе результатов возврата из этой же функции для предыдущего (того, что больше или меньше) значения аргумента.
Когда метод вызывает себя самостоятельно, он носит название «рекурсивный алгоритм» или «вызов». Каждый раз будут запоминаться прошлые значения внутренних локальных переменных, а также полученных в результате расчетов параметров функций.
41 Рекурсия в Python. Рекурсивная функция Часть 1
Для того, чтобы каждый шаг рекурсивного вызова отличался от прошлого, корректируются параметры функции. Минимум – один из них. Останавливается процесс соответствующих алгоритмов тогда, когда корректируемые значения достигают некоторого «лимита». Пример – обработка последнего массивного элемента.
Выражение в компьютерах
Программеры сталкиваются с рекурсивными алгоритмами в структурах данных:
- Графы. Эти объекты рассматривают в качестве совокупности отдельных узлов и подграфов (наименьших из имеющихся).
- Строки, состоящие из первого символа и подстроки. А именно – самой маленькой строчки.
Также рассматриваемое понятие встречается в шаблонах проектирования. Пример – декораторы. Его объекты могут включать в себя другие составляющие, которые тоже выступают в качестве декораторов. А еще в виде функций. Последний вариант является самым распространенным.
Особенно при написании машинных кодов.
Основным правилом операции служит следующий принцип: до рекурсивного вызова обязательно должна стоять проверка на возврат.
Важные термины
Для лучшего понимания темы необходимо уяснить следующие понятия:
- Рекурсивный порядок действий – тот, в определении которого имеется прямой/косвенный вызов того же метода.
- Рекурсивная функция – математическое уточнения интуитивного понятия рассматриваемого выражения.
- Адаптивный рекурсивный алгоритм – порядок действий, при которых благодаря рекурсивности во внимание принимаются индивидуальные черты решаемой задачи из области своего определения.
- Базис – предположение, которое определяет начальные обстоятельства или «картину» происходящего в момент завершения. Здесь описывается элементарный случай, при котором удается сразу получить ответ.
- Шаг – принцип, тело которого содержит в качестве подцели вызов определяемого предиката.
- Подпрограммы – все то, что располагается внутри рекурсивных операций.
Теперь можно подумать, какие у рекурсии имеются разновидности. Их не так много, но каждый вариант развития событий предусматривает собственные нюансы.
Стратегия
Но для начала стоит рассмотреть так называемый рекурсивную стратегию. Это – общий случай, согласно которому происходит реализация поставленной задачи. Состоит из нескольких шагов:
- упорядочивание информации;
- решение меньшей части проблемы;
- поиск и реализация решения большей части поставленной задачи.
Для лучшего понимания стоит рассмотреть наглядный пример, но о нем позже. Ведь рекурсия и ее методы бывают разными. И каждый предусматривает какие-то свои нюансы.
Разновидности рекурсии
Рекурсивные методы классифицируются по-разному: по своей сложности или «хвостовой части». Поэтому условно разделить соответствующий элемент можно на несколько крупных категорий.
Простая
Это – функция, которая содержит вызов иных операций и методов. Способна вызывать себя самостоятельно. Никаких парадоксов. Компьютер будет последовательно выполнять команды, а если встретится вызов процедуры, займется ей.
Procedure Rec(int n); Begin If n>0 then; Rec(n-1); Writeln(n); End;
Предложенный код – пример простой рекурсии. Но есть и другие варианты развития событий. Решения задачи иногда требуют более «запутанных» алгоритмов.
Сложная
Данном случае одна функция вызывает другую. Вторая ответно занимается вызовом первой. При подобных обстоятельствах первая операция должна вызывать ту, что еще не описана. Для того, чтобы справиться с поставленной задачей, используются так называемые опережающие описания.
Procedure A(int i); //заголовок первой операции – опережающее описание Procedure B(int i); //опережающая «характеристика» второго действия Procedure A(int i); //полное описание основной операции A Begin Writeln(i); B(i-1); End; Procedure B(int i); //полное описание основной операции B Begin Writeln(i); If i
Если попытаться представить наглядно предложенные рекурсивные функции, то простой вариант – это уроборос. Сложный – детский стишок, в котором «волки с перепуга, скушали друг друга». Достаточно наглядно представить этот процесс и двух волков, чтобы понять, о чем речь.
Хвостовая
Хвостовой рекурсия будет, если соответствующий вызов окажется последним действием функции перед тем, как произойдет возврат результата. То есть, окажется в «хвосте» описываемого алгоритма:
Def fact_tailrec(n, result 1); If n=0; Return result 1 Else Return fact_tailtec(n-1, result*n)
Этот код актуален для факториала.
Не обязательно метод хвостового типа будет также считаться рекурсивным. Он способен вызывать иные функции, осуществлять взаимную рекурсию или иные, более сложные схемы. Каноничный пример взаимной рекурсии:

Тут вызовы функций располагаются в «хвосте». Более простым примером обойтись нельзя. Связано это с тем, что представленные коды используют только один вызов в каждой операции. Кодификация усложняется, когда необходимо осуществлять множественные обращения. Пример – вычисление числа Фибоначчи.
Не хвостовая
Если же вызовы не являются последними в задействованной функции, она называется не хвостовой. Таких примеров очень много. Все, что не относится к хвостовому виду.
Классификация по записи
Рекурсивная функция может вызывать сама себя. Из-за этого приходится повторно выполнять имеющиеся в ней указания. Происходит операция, подобная работе цикла. Записываться такой элемент может разными методами:
- Префиксным способом. Сначала происходит рекурсивный вызов, только потом – необходимые действия.
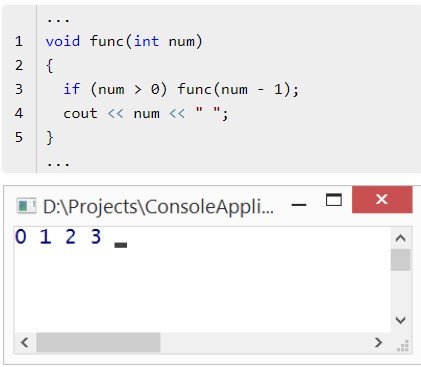
- 2. Постфиксной записью. При подобных обстоятельствах на первый план выходят те или иные алгоритмы/манипуляции. Лишь после программист должен сделать вызов рекурсивной функции.
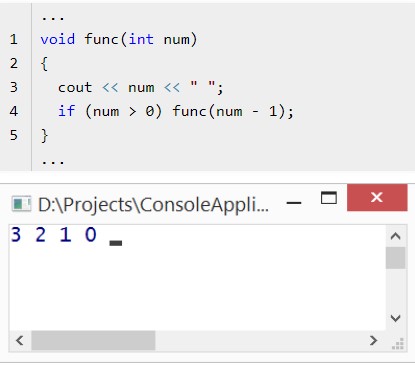
Стоит обратить внимание на некоторые «частные» случаи. Они помогают заменить рассматриваемые типы записей на более простые.
Итерирование
Отдельный вид рекурсии – когда в его основе находятся рекуррентные соотношения. Они имеют вид:
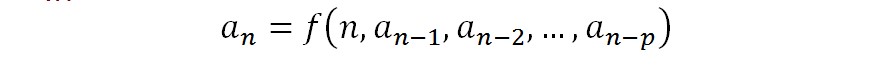
Здесь каждый элемент последовательности выражается через p предыдущих членов. Для того, чтобы получить тот или иной результат, потребуется повторение обновления значений этой самой последовательности. Соответствующее действие называют итерацией, а сам процесс «воспроизведения» — итерирование.
Итерация – осуществление обработки информации, при которой предпринимаемые манипуляции повторяются много раз. Вызов элементов массива (то есть, самих себя) в описываемом случае не осуществляется. В рекурсии – да.

При вызове функций осуществляется некоторое количество допрасходов, связанных с передачей управления и аргументов, возврата вычисленных значений. Итерационная операция в случае с факториалом (пример выше) окажется быстрее recursion. Итерация c рекурсией не всегда совместимы.
Внимание: если в основе рекурсивной операции лежит единственное условие «вызвать саму себя», ее удастся с легкостью заменить итерационным циклом.
Алгоритмы рекурсии – анализ
Когда происходит анализ циклических функций, осуществляется расчет трудоемкости итераций и их численность в самом плохом, хорошем и среднем случае. Но с рекурсией подобный расклад не работает. Связано это с тем, что в конечном итоге получится рекуррентное соотношение. По ним сложность оценить невозможно.
Поэтому на практике используются различные способы реализации поставленной задачи:
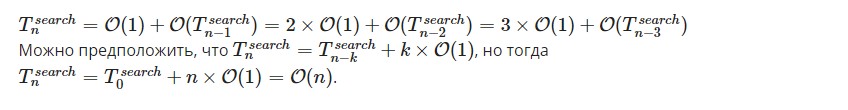
- Подстановка (метод итераций). Последовательно заменяются рекуррентные части в выражениях для того, чтобы получить новые. Операция не прекращается до тех пор, пока не будет понят общий принцип, а также пользователь не сможет переписать его нереккурентной формулой. В примере ниже выведена формула, но первый шаг – это предположение. Нет никаких доказательств соответствия операции рекуррентному выражению.
- 2. Математическая индукция. Доказывает истинность некоторого утверждения, состоящего из двух шагов. Первый – это доказательства утверждения для частных случаев (одного или нескольких). Второй – из истинности основополагающего утверждения (индуктивной гипотезы) и частных случаев выводят подтверждение последующих шагов.
- 3. Общий. В нем каждое условие для случая в формуле доказано формально. Требуется определить случай основной теоремы, согласно которому обнаружится соответствие рекуррентного соотношения.
Но приведенные примеры преимущественно встречаются в теории. В реальной жизни они не имеют места. Для лучшего понимания рекурсии стоит изучить наглядный практический пример. Он пригодится каждому пользователю.
Пример из практики
Решения рекурсивного характера – условие, которое не так трудно обнаружить на практике. Но жизненные примеры весьма проблематично представить такими, чтобы их можно было изобразить итеративным способом.
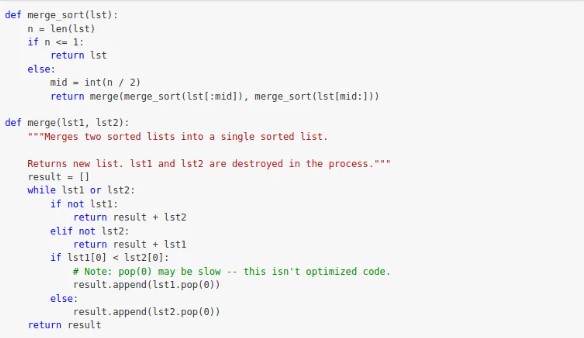
Это – наглядный образец сортировки посредством слияния. Используемый язык программирования – Python. Чем-то напоминает обратный ход дерева – сначала требуется пойти рекурсивно влево, после – вправо, далее – скомбинировать полученные результаты. Подобные вариации в «обычный» код перерабатываются с трудом. Но в практике применяются достаточно часто.
Сортировка посредством слияния – множественная рекурсия, которая была рассмотрена равным образом как с числом Фибоначчи.
Теперь основные моменты, связанные с рекурсией в программировании, понятны. Более углубленное изучение темы основывается на составлении различных примеров непосредственно на языках программирования.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Источник: otus.ru
Как работает рекурсия – объяснение в блок-схемах и видео
Представляю вашему вниманию перевод статьи Beau Carnes How Recursion Works — explained with flowcharts and a video.

«Для того чтобы понять рекурсию, надо сначала понять рекурсию»
Рекурсию порой сложно понять, особенно новичкам в программировании. Если говорить просто, то рекурсия – это функция, которая сама вызывает себя. Но давайте попробую объяснить на примере.
Представьте, что вы пытаетесь открыть дверь в спальню, а она закрыта. Ваш трехлетний сынок появляется из-за угла и говорит, что единственный ключ спрятан в коробке. Вы опаздываете на работу и Вам действительно нужно попасть в комнату и взять вашу рубашку.
Вы открываете коробку только чтобы найти… еще больше коробок. Коробки внутри коробок и вы не знаете, в какой из них Ваш ключ. Вам срочно нужна рубашка, так что вам надо придумать хороший алгоритм и найти ключ.
Есть два основных подхода в создании алгоритма для решения данной проблемы: итеративный и рекурсивный. Вот блок-схемы этих подходов:
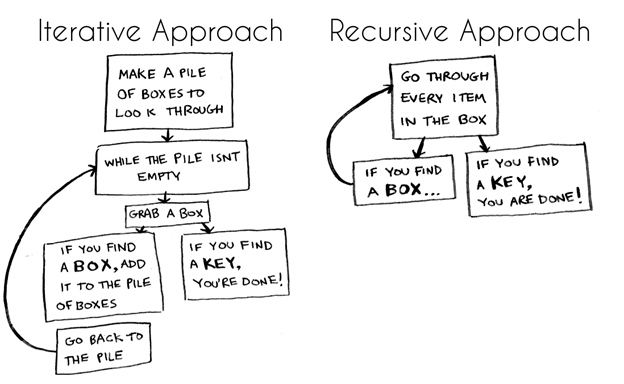
Какой подход для Вас проще?
В первом подходе используется цикл while. Т.е. пока стопка коробок полная, хватай следующую коробку и смотри внутрь нее. Ниже немного псевдокода на Javascript, который отражает то, что происходит (Псевдокод написан как код, но больше похожий на человеческий язык).
function look_for_key(main_box) < let pile = main_box.make_a_pile_to_look_through(); while (pile is not empty) < box = pile.grab_a_box(); for (item in box) < if (item.is_a_box()) < pile.append(item) >else if (item.is_a_key()) < console.log(«found the key!») >> > >
В другом подходе используется рекурсия. Помните, рекурсия – это когда функция вызывает саму себя. Вот второй вариант в псевдокоде:
function look_for_key(box) < for (item in box) < if (item.is_a_box()) < look_for_key(item); >else if (item.is_a_key()) < console.log(«found the key!») >> >
Оба подхода выполняют одно и тоже. Основный смысл в использовании рекурсивного подхода в том, что однажды поняв, вы сможете легко его читать. В действительности нет никакого выигрыша в производительности от использования рекурсии. Порой итеративный подход с циклами будет работать быстрее, но простота рекурсии иногда предпочтительнее.
Поскольку рекурсия используется во многих алгоритмах, очень важно понять как она работает. Если рекурсия до сих пор не кажется Вам простой, не беспокойтесь: Я собираюсь пройтись еще по нескольким примерам.
Граничный и рекурсивный случай
То, что Вам необходимо принять во внимание при написании рекурсивной функции – это бесконечный цикл, т.е. когда функция вызывает саму себя… и никогда не может остановиться.
Допустим, Вы хотите написать функцию подсчета. Вы можете написать ее рекурсивно на Javascript, к примеру:
// WARNING: This function contains an infinite loop! function countdown(i) < console.log(i) countdown(i — 1) >countdown(5); // This is the initial call to the function.
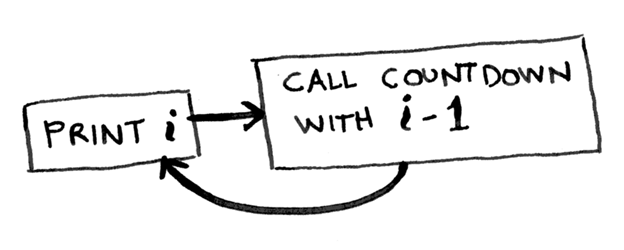
Эта функция будет считать до бесконечности. Так что, если Вы вдруг запустили код с бесконечным циклом, остановите его сочетанием клавиш «Ctrl-C». (Или, работая к примеру в CodePen, это можно сделать, добавив “?turn_off_js=true” в конце URL.)
Рекурсивная функция всегда должна знать, когда ей нужно остановиться. В рекурсивной функции всегда есть два случая: рекурсивный и граничный случаи. Рекурсивный случай – когда функция вызывает саму себя, а граничный – когда функция перестает себя вызывать. Наличие граничного случая и предотвращает зацикливание.
И снова функция подсчета, только уже с граничным случаем:
function countdown(i) < console.log(i) if (i else < // recursive case countdown(i — 1) >> countdown(5); // This is the initial call to the function.
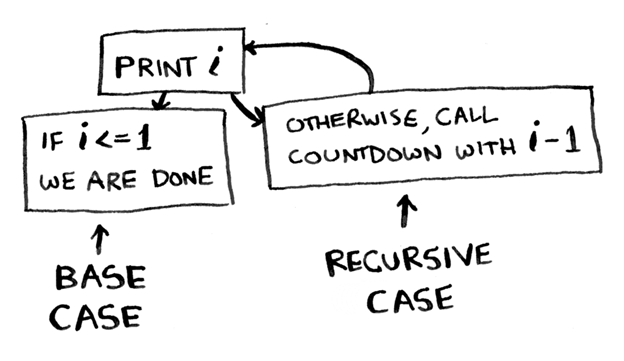
То, что происходит в этой функции может и не быть абсолютно очевидным. Я поясню, что произойдет, когда вы вызовете функцию и передадите в нее цифру 5.
Сначала мы выведем цифру 5, используя команду Console.Log. Т.к. 5 не меньше или равно 1, то мы перейдем в блок else. Здесь мы снова вызовем функцию и передадим в нее цифру 4 (т.к. 5 – 1 = 4).
Как работает рекурсия в программировании
Пытаясь примитивно объяснить рекурсию в программировании, многие ошибочно представляют ее по аналогии с зацикленным видеофрагментом типа гифок. И потому возникают вопросы о целесообразности ее использования, ведь программный код по сути прописывает пошаговые действия. Так зачем же нужен этот «уроборос»?
Но если все же вернуться к терминам программирования, то рекурсию можно трактовать как функцию, которая вызывает сама себя. И это объяснение кажется почти парадоксальным: ведь как найти решение проблемы, используя ее же решение?! И тем не менее, рекурсия в программировании используется весьма активно. И вот почему.
Что такое рекурсия в программировании простыми словами
Рекурсия представляет собой методологию решения проблем, в которой вы выполняете задачу по частям, не рассматривая ее целиком. При этом задача уменьшается или становится проще. Таким образом, рекурсия является не просто практикой в программировании, а целым философским подходом.
Рекурсию можно использовать и для достижения простейших бытовых целей. К примеру, перед вами стоит задача написания 500 слов. В этом случае вы можете поставить себе цель создавать по 50 лексем всякий раз, когда начинаете работать. Вначале вы пишете это их количество, остается 450.
Далее вы проделываете то же самое, и следующая задача – уже 400 слов. Тем самым при каждом подходе вы не решаете проблему полностью, но уменьшаете ее объем.
Для вас подарок! В свободном доступе до 09.07 —>
Скачайте ТОП-10
бесплатных нейросетей
для программирования
Помогут писать код быстрее на 25%
Чтобы получить подарок, заполните информацию в открывшемся окне
Если речь идет о статье, то код может выглядеть следующим образом:
if words left > 0:
words_left = words_left — 100
Данный алгоритм можно создать итеративно:
while words_left > 0:
words_left = words_left — 100
Говоря о вызове функции write_words(1000), в каждой из перечисленных реализаций стоит отметить, что в обоих случаях можно заметить идентичное поведение. Делая выбор за и против рекурсии в программировании, нельзя не отметить, что любая задача, которую можно решить с ее помощью, может быть разгадана и с использованием итерации (циклы for и while). Но в чем же тогда преимущество данного метода?
Дело в том, что существуют проблемы, которые гораздо проще разрешить посредством рекурсии. В некоторых случаях она показывает повышенную эффективность, в других — бо́льшую читаемость, а в определенных ситуациях банально занимает меньше времени при реализации. Есть такие структуры данных, которые сами по себе очень подходят для рекурсивных алгоритмов (например, деревья).
Некоторые языки программирования не предполагают наличие цикла. Они являются сугубо функциональными и всецело зависят от применения рекурсии при итеративном решении проблем.
В принципе, программист может и не понимать рекурсии. Однако специалист высокого уровня все же должен осознавать суть данной методики. Плюс ко всему, вы сможете применять этот подход в других областях, эффективно решая различные задачи.
Итак, рекурсия в программировании предполагает дифференцирование больших задач на более мелкие. Выполняя один шаг, вы уменьшаете основную проблему и после этого повторяете аналогичное действие. В конечном итоге проблема уменьшается настолько, что остается выполнить одно простое действие, которое принято называть базовым случаем.
Узнай, какие ИТ — профессии
входят в ТОП-30 с доходом
от 210 000 ₽/мес
Команда GeekBrains совместно с международными специалистами по развитию карьеры подготовили материалы, которые помогут вам начать путь к профессии мечты.
Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее будущее!
Скачивайте и используйте уже сегодня:

Александр Сагун
Исполнительный директор Geekbrains
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Получить подборку бесплатно
Уже скачали 21541
Таким образом простейшее решение базового случая, в совокупности со всеми действиями, которые вы осуществили перед этим, представляет собой разгадку основной проблемы.
Примеры алгоритмов рекурсии в программировании
Понять, что такое рекурсия в программировании, можно с помощью простых примеров. При помощи этого алгоритма проблема разделяется на составляющие, которые структурно представляют собой такие же задачи, как и основная. Единственное отличие — они являются упрощенными по сравнению с исходной проблемой. Чтобы решить эти подзадачи, функция вызывается рекурсивно.
Результаты произведенных систематических действий объединяются тем или иным способом. Но расчленение проблемы имеет смысл только в том случае, если она достаточно сложна и не может быть решена в один заход.
Скажем, если стоит цель обработки массива, то во многих случаях ее можно редуцировать к последовательной однотипной обработке его составляющих. Исходя из определения рекурсии в программировании, становится очевидным, что разделение осуществляется вплоть до момента, когда эти части не станут наиболее легкими. Иными словами, подзадачи должны быть настолько элементарными, чтобы их можно было решить, не прибегая к очередному упрощению.
Поиск элемента массива:
начало; search(array, begin, end, element)
; выполняет поиск элемента со значением element в массиве array между индексами begin и end
если begin > end
результат := false; элемент не найден
иначе если array[begin] = element
результат := true; элемент найден
результат := search(array, begin+1, end, element)
конец; вернуть результат
Тем самым алгоритм дифференцирует исходный массив на 2 составляющие — первый элемент и массив из оставшихся частей. Происходит выделение 2 простых случаев, при которых нет необходимости в дальнейшем разборе, т. е. либо когда была произведена обработка всей совокупности составляющих, либо когда первый элемент является искомым.
В алгоритме поиска можно дифференцировать массив и другим способом, к примеру, на две равные части. Однако такой подход обычно менее результативен. Когда массив отсортирован, его имеет смысл разделять на две одинаковые части, ведь на каждом шаге численность обрабатываемых данных можно разобрать на два фрагмента.
Двоичный поиск в массиве осуществляется после того, как была произведена его сортировка. На любом из этапов работы происходит сравнение между искомым элементом и значением, которое располагается в средней части массива. После получения результатов такого сравнения левая или правая части могут быть отброшены. Например:
начало; binary_search(array, begin, end, element)
; выполняет поиск элемента со значением element
; в массиве, упорядоченном по возрастанию, массиве array
; между индексами begin и end
если begin > end
конец; вернуть false — элемент не найден
mid := (end + begin) div 2; вычисление индекса элемента посередине рассматриваемой части массива
если array[mid] = element
конец; вернуть true (элемент найден)
результат := binary_search(array, mid+1, end, element)
результат := binary_search(array, begin, mid, element)
конец; вернуть результат
Вычисление чисел Фибоначчи
Ряд чисел Фибоначчи определяется рекуррентным соотношением. Проще говоря, каждое последующее число вычисляется на основе предыдущих:
конец; вернуть 0
конец; вернуть 1
результат := fib_1 + fib_2
конец; вернуть результат
Рекурсивная стратегия
В зависимости от того, какую задачу необходимо решить, стратегия рекурсивного метода может отличаться. Вместе с тем существует общая тактика, которую можно использовать в качестве ориентира:
Упорядочивание данных
Это фундаментальный этап решения задач при помощи рекурсивного метода, однако многие пренебрегают тщательностью его выполнения. Неважно, какие именно данные используются — числа, строки, списки, бинарные древа или же люди, – вам в любом случае следует отыскать оптимальный порядок элементов.
Только до 6.07
Скачай подборку материалов, чтобы гарантированно найти работу в IT за 14 дней
Список документов:

ТОП-100 площадок для поиска работы от GeekBrains

20 профессий 2023 года, с доходом от 150 000 рублей

Чек-лист «Как успешно пройти собеседование»
Чтобы зарегистрироваться на бесплатный интенсив и получить в подарок подборку файлов от GeekBrains, заполните информацию в открывшемся окне
Это не только позволит лучше понять задачу, но и сделает ее решение значительно проще. В зависимости от текущей проблемы этот порядок будет отличаться. Однако сначала рекомендуется рассмотреть самые очевидные варианты сортировки.
Если речь идет о числах, то можно произвести упорядочивание по величине, о строках и списках — по длине, бинарные древа систематизируются по глубине. Если же выстраиванию подвергаются люди, то вариантов гораздо больше: по росту, по весу, по специализации и т. д. При этом выбранный метод упорядочивания должен соответствовать тому, насколько сложной является проблема.
Вслед за тем, как вы осуществите упорядочивание данных, необходимо подумать об этом, как о чём-то, что вы можете сократить. Формализация порядка может выглядеть следующим образом:
0, 1, 2, …, n – для чисел (т. е. для int данных d, степень(d) = d);
[], [■], [■, ■], …, [■, …, ■] – для списков (len = 0, len = 1, …, len = n и т. д. для списка d, степень(d) = len(d)).
Идя справа налево, вы будете передвигаться от большой части задачи (скопления базовых случаев) к небольшим фрагментам (базовым случаям).
Решаем малую часть проблемы
Чаще всего данный этап является наиболее простым. Произведя упорядочивание, необходимо определить самые мелкие задачи, а затем выбрать способ работы над ними. Как правило, имеется возможность отыскать простейшее решение: в случае reverse(s), как только мы дойдём до len(s) == 0, имея при этом reverse(»), это будет знаком, указывающим на то, вы нашли ответ, так как реверс пустой строки ничего не даст.
Проще говоря, вы опять увидите пустую строку, ведь у вас не будет символов, которые можно еще передвигать.
Выявив решение для базового случая и определившись с порядком, уровень сложности общего случая будет снижаться в зависимости от структурности данных, которые подвергаются обработке по мере передвижения в направлении базовых случаев. Здесь нужна внимательность, дабы не упустить из виду ни один из последних.
В конце концов, их называют базовыми не просто так: именно они являются каркасом порядка. Если вы работаете над непростой рекурсивной проблемой, то не допускайте популярную ошибку в виде пропуска маленького шага. Зачастую это влечёт за собой проблему получения данных, не имеющих никакого смысла, и огрехи в коде.
Переходим к общим случаям
Этот шаг предполагает обработку данных, при которой вы движетесь вправо (в сторону высокого уровня). Чаще всего рассматриваются данные произвольной степени, и осуществляется поиск методики решения задачи за счёт ее постепенного упрощения. Результатом такого действия является выражение, которое по своей структуре является той же самой задачей, но как бы в уменьшенном масштабе.
В качестве примера можно рассмотреть работу с числами Фибоначчи. Сначала было взято произвольное значение n, а затем мы произвели упрощение fib(n) до fib(n-1) + fib(n-2). Полученный результат представляет собой выражение, которое включает в себя два варианта исходной задачи, но в более простом виде (n-1 и n-2 соответственно).
Популярные статьи





В случае с алгоритмом reverse вы можете рассмотреть произвольную строку с длиной n, и предположить, что наша reverse-функция применима для любой строки с длиной меньше n. Это можно использоваться при решении задач для строки с длиной n. С этой целью вам нужно сделать реверс строки, передвигая все, за исключением последнего символа. После этого следует вставить последний символ в начало. Код будет выглядеть следующим образом:
reverse(string) = reverse(string[-1]) + reverse(string[:-1]),
string[-1] — последний символ;
string[:-1] — строка без последнего символа (питонизм).
В этом коде reverse(string[:-1]) представляет собой последний член функции и выступает в качестве исходной задачи, однако работает он со строкой длины n-1.
Если вы возьмете данное решение для функции reverse, то вы получите вот такой результат:
if len(string) == 0:
return string[-1] + reverse(string[:-1])
Перед программистами нередко встаёт проблема рассмотрения нескольких рекурсивных случаев, потому что данные определённого типа могут принимать различные формы. Однако это всецело зависит от самой задачи.
В качестве примера рассмотрим случай, при котором вы собираетесь сгладить список элементов, некоторые из которых сами могут являться такими же перечнями. Вам следует различать ситуации, когда объект, который вы вытаскиваете из списка, является отдельным элементом, и когда – подсписком. Это влечет за собой как минимум два самостоятельных рекурсивных случая.
Учтите, что невозможно улучшить навыки в рекурсии без практики. На просторах Сети вы можете отыскать сотни примеров различных задач, которые можно решить при помощи данного метода. Рано или поздно вы овладеете им, но при появлении каких-либо проблем вы всегда можете переключиться на итерацию.
Рекурсивный метод применим как в программировании, так и в быту. Если задача не подходит для такого решения, то ничего страшного. Набравшись опыта, вы станете быстрее понимать, какую проблему можно решить рекурсивно, а какую итеративно.
Итеративные и рекурсивные программы имеют одни и те же способности решения задач. Иными словами, любую программу первого вида можно переписать в варианте второго, и наоборот. Но учтите, что если сравнивать итеративное и рекурсивное решения, то второе является более требовательным к используемой памяти. В этом случае все функции остаются в стеке вплоть до момента, пока не будет достигнут наилучший вариант.