Что такое программа действий и план действий в математике

Понять, какое описание последовательности действий может быть названо алгоритмом, какие бывают свойства у алгоритма.

Научиться отличать алгоритм от плана действий (описания последовательности действий).

Понять

Чтобы решить задачу, надо знать, что для этого следует делать, как делать и в каком порядке. Рассмотрим на примере.

Пусть нам надо решить простую математическую задачу:

Лена купила 4 тетради по 20 рублей и 2 авторучки по 15 рублей. Сколько стоила её покупка?

Рассмотрим два варианта плана действий, которые необходимо выполнить, чтобы ответить на вопрос задачи.

1. Определи отдельно стоимость тетрадей и стоимость авторучек.
2. Определи стоимость покупки.

1. Умножь стоимость одной тетради на количество тетрадей.
2. Умножь стоимость одной авторучки на количество авторучек.
3. Найди сумму полученных произведений.

Вариант № 1 и вариант № 2 — это различные описания последовательности мысленных действий, которые надо исполнить, чтобы решить задачу. Чем второй вариант плана действий отличается от первого?

Математика 5 Порядок выполнения действий

Оба варианта — это последовательности шагов-инструкций. Вариант № 1 состоит из двух шагов, а вариант № 2 — из трёх. Но это несущественное отличие.

Существенное отличие заключается в содержании шагов-инструкций.

В первом случае инструкции (команды исполнителю плана) неконкретные, нечёткие. Не каждый школьник может их выполнить.

Во втором варианте инструкции более чёткие, конкретные. Они понятны каждому ученику четвёртого класса. Выполнив их, можно получить ответ на вопрос задачи.

Один из этих вариантов можно назвать алгоритмом, а другой — нет. Какой же из них — алгоритм?

Алгоритмом мы можем назвать такое описание последовательности действий, которое обладает определёнными свойствами. Вот эти свойства:

Всем пяти свойствам удовлетворяет вариант № 2 плана действий. Значит, эта последовательность инструкций есть алгоритм определения стоимости покупки предметов двух наименований.

• состоит из отдельных инструкций;
• состоит из конечного числа инструкций;
• является понятной исполнителю; исполнение приводит к ожидаемому результату;
• позволяет решить не одну задачу, а целый класс подобных задач.

Рассмотрим алгоритм определения площади прямоугольника. Обозначим площадь буквой S. Математики нашли алгоритм нахождения площади прямоугольника:

1. измерь длину А прямоугольника;
2. измерь ширину В прямоугольника;
3. определи площадь S как произведение длины А на ширину В.

Этим алгоритмом пользуются все люди, когда хотят найти площадь земельного участка, жилую площадь дома, площади стен или прямоугольных окон, крыш при его строительстве или ремонте.

Выполни

1. Найди площадь рабочей поверхности твоей парты, воспользовавшись алгоритмом:

1. измерь длину поверхности парты: А;
2. измерь ширину поверхности: В;
3. найди площадь как произведение длины на ширину: S = А • В;
4. запиши результат на носителе информации.

Главное

• Алгоритм — это подробный план последовательности действий, описывающий решение задачи.
• Последовательность шагов-инструкций может быть названа алгоритмом, если она обладает свойствами: число шагов известно и конечно, смысл инструкций понятен, ожидаемый результат известен, годится для решения целого класса задач.
• Алгоритм — это модель процесса решения задач.

Знать

1. Как можно описать план решения задачи?
2. Любой ли план действий можно назвать алгоритмом? А какой? Расскажи.
3. Зачем люди составляют и исполняют алгоритмы? Приведи пример из своей жизни.
4. Что ты знаешь про алгоритм? Расскажи на своём примере.
5. Назови свойства последовательности инструкций, которую можно назвать алгоритмом.

Уметь

Выполни задания в рабочей тетради № 2.

Порядок выполнения действий в выражениях. Числовые выражения

Выполни на компьютере задания к параграфу из раздела УМЕТЬ компакт-диска.

Прочитай на досуге в книге «Расширь свой кругозор» текст «Существует ли алгоритм создания модели?».

Источник: tepka.ru

«Программа действий. Алгоритм». 2 класс. УМК «Школа 2100»
план-конспект урока по математике (2 класс) на тему

Презентация на тему Разработка плана действий и его запись

Слайд 4План действий в виде списка
Простейший способ записи плана действий может

быть
выполнен в виде столбца действий или списка.
Задача1:выполнить действие – кормление

1) взять батон хлеба;
2) отломить кусочек;
3) найти голубя;
4) бросить кусочек недалеко от птицы.

Слайд 5План действий в виде списка
Каждый из 4 пунктов может быть

представлен в виде более простых действий получим список:

хлеба:
найти магазин;
зайти в магазин;
найти хлебный отдел;
узнать цену хлеба;
проверить сколько денег в кошельке;
купить хлеб;
2) отломить кусочек:
взять батон в руку;
отделить небольшой кусочек от батона;
3) найти голубя:
выйти из магазина;
дойти до парка;
найти солнечное место, где любят греться голуби;
4) бросить кусочек недалеко от птицы:
подойти к голубям не слишком близко;
кинуть хлеб недалеко от птиц.

Слайд 6Задание №1
Приведите любой пример плана действий
без разложения на более простые

элементы, и с разложением.

Слайд 7План действий в виде схемы
Задача2: Маша и Лиза играют в

игру. Маша задумывает правила преобразования информации. Лиза может предлагать Маше

любые тексты и узнавать результаты преобразования. Вопросы Лизы и ответы Маши в этой игре:
а б ; мама нбнб; весна гётоб
Какое же правило задумала Маша?

Слайд 8План действий в виде схемы
Решение:
Маша каждую букву заменяет на

следующую по алфавиту.
Проверим наше предположение на примерах 2 и 3.

мама нбнб весна гётоб
м = н; а= б; м=н; а=б в=г; е=ё; с=т; н=о; а=б

Наше предположение верно.
В результате мы установили, что схема преобразования информации –
замена каждой буквы в исходном тексте на следующую по алфавиту.

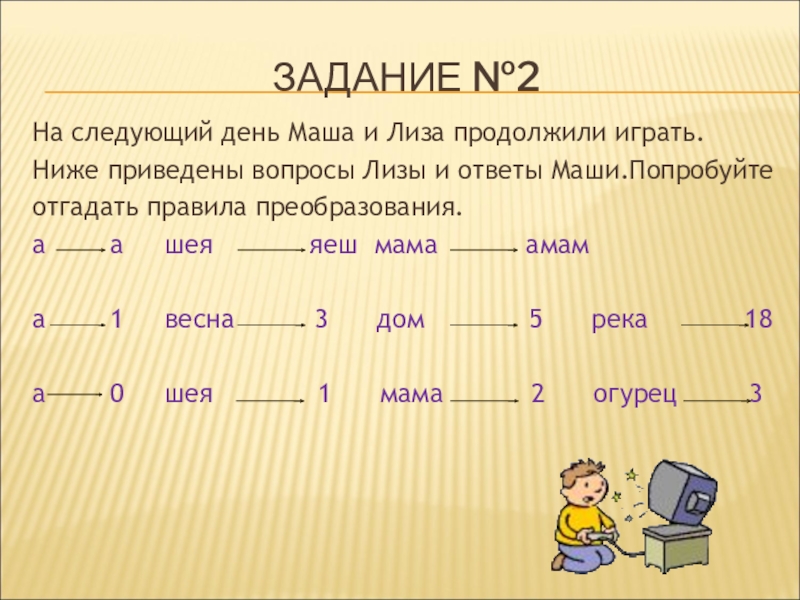
Слайд 9Задание №2
На следующий день Маша и Лиза продолжили играть.
Ниже

приведены вопросы Лизы и ответы Маши.Попробуйте
отгадать правила преобразования.
а

а шея яеш мама амам

а 1 весна 3 дом 5 река 18

а 0 шея 1 мама 2 огурец 3

Слайд 10План действий в виде таблицы
Задача3:Два солдата подошли к реке, по

которой на лодке катаются двое мальчиков. Как солдатам переправиться на

другой берег, если лодка вмещает только одного солдата или двух мальчиков, а солдата и мальчика уже не вмещает?
Обозначения: М1 и М2 – мальчики, С1 и С2 – солдаты, стрелка
направление переправы. План переправы в виде списка:
М1 и М2
М1
С1
М2
М1 и М2
М1
С2
М2

Слайд 11План действий в виде таблицы

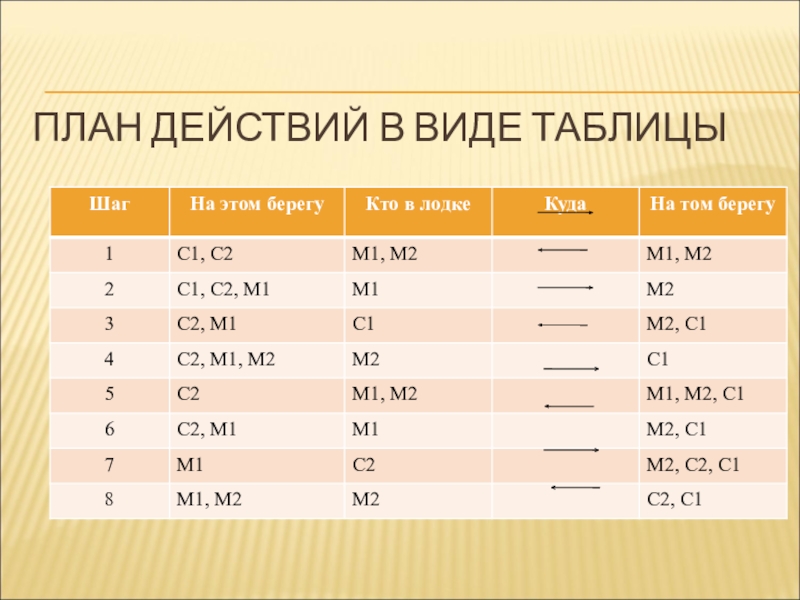
Слайд 12Задачи на
сообразительность

Слайд 13Возле школы растут 6 деревьев: сосна, береза, липа, тополь, ель

и клен. Какое из деревьев самое высокое и самое низкое,

если известно, что береза ниже тополя, липа выше клена, сосна ниже ели, липа ниже березы, сосна выше тополя?

Слайд 145 одноклассников: Аня, Саша, Лена, Вася и Миша стали победителями

школьных олимпиад по истории, математике, информатике, литературе и географии. Известно,

что
Победитель по информатике учит Аню и Сашу работать на компьютере,
Лена и Вася тоже заинтересовались информатикой,
Саша всегда побаивался истории,
Лена, Саша и победитель по литературе занимаются плаванием,
Саша и Лена поздравили победителя по математике,
Аня сожалеет, что у нее мало времени на литературу.

Источник: theslide.ru