Математическая формулировка задачи: Вычислить и вывести на печать значение функции y. Исходные данные x, a и b ввести с клавиатуры.
- Листинг программы.
writeln (’ введите x,a, b ’);
Вопросы для самоконтроля
- Что такое программа?
- Какие символы могут содержать имена переменных?
- Какие типы стандартные переменных допустимы на языке Паскаль?
- Сколько байт памяти занимают переменные типа real?
- Из каких частей состоит структура программы на Паскале.
- Что определяет объем памяти, отводимой под каждую переменную?
- Что такое оператор?
- Какие типы операторов допустимы на Паскале?
- Как операторы отделяются друг от друга?
- Для чего используются комментарии в программе?
8.11. Методические указания для выполнения практического задания №4. «Следования»
Цель работы: Ознакомиться со структурой программы на языке Паскаль, основными операторами, алгоритмами линейной структуры..
Линейные операторы. Тема
Задание:
1. В приложении 5 выбрать вариант задания.
2. Выполнить практическое задание №4, используя пример программы линейной структуры.
3. Составить блок-схему алгоритма.
4. Написать программу и отладить ее по заранее подготовленному тесту.
5. Оформить работу в тетради для практических работ.
6. Результат выполнения программы предъявить преподавателю.
7. Ответить на вопросы самоконтроля.
8. Защитить выполненную работу у преподавателя.
Приложение 5. Таблица вариантов заданий
| Вычислить и вывести на печать значение функции Y. Исходные данные x, a и b ввести с клавиатуры. |
Ветвления
Очень часто встречаются ситуации, когда требуется выбрать между двумя или более вариантами действий в зависимости от заданного условия. Такая алгоритмическая конструкция называется ветвлением.
Источник: mykonspekts.ru
Линейные операторы
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y=A(x) или y=Ax.
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 
и 
соответственно. Пусть задано отображение
Python. Линейный алгоритм
| y=Ax, | (1) |
где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
 , |
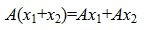(2) |
 . |
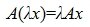Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов
в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.
Пусть x − произвольный элемент в R. Тогда
 |
(3) |
является разложением x в по базису .
Применим оператор A к базисным векторам :
 |
(4) |
где aij − координаты полученного вектора в базисе .
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
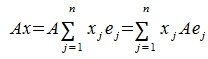
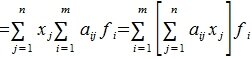
Сделаем следующее обозначение:
 |
(6) |
Тогда равенство (5) примет следующий вид:
 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты yi, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента xj, j=1,2. n с коэффициентами aij i=1,2. m; j=1,2.
n.
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
| y=Ax. | (9) |
Матрица A называется матрицей линейного оператора в заданных базисах и .
2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
| Cx=Ax+Bx, x∈R, | (10) |
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej=Aej+Bej= | n | (aij+bij)ej |
| ∑ | ||
| j=1 |
Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.
| C=A+B. | (11) |
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx=A(Bx), x ∈ R. | (12) |
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
| y=Bx, z=Ay, z=Cx |
можно записать в виде матричных равенств
| y=Bx, z=Ay, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=A(Bx)=(AB)x. |
Учитывая произвольность х, получим
| C=AB. | (13) |
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx=λ ( Ax) | (14) |
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
| y=Ax, z=λy, z=Cx |
можно записать в виде матричных равенств
| y=Ax, z=λy, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=λ(Ax)=(λA)x. |
Учитывая произвольность х, получим
| C=λA. | (15) |
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
| Ox=0. |
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
| −A=(−1)A. |
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
Источник: matworld.ru
ЛАБОРАТОРНАЯ РАБОТА № 1 Разработка алгоритмов и программ линейной структуры
Разработка алгоритмов и программ линейной структуры
Цель: освоить методы разработки алгоритмов и программирования задач линейной структуры.
Краткие теоретические сведения
Алгоритм линейной структуры – это алгоритм, в котором все действия выполняются последовательно друг за другом и только один раз. Блок-схема алгоритма представляет собой последовательность блоков, которые располагаются сверху вниз в порядке их выполнения. Все промежуточные или исходные данные влияния на направление процесса выполнения не оказывают.
Пример. Вычислить высоты треугольника со сторонами a, b, c, используя формулы:
h = 2
h = 2
h = 2
p ( p — a )( p — b )( p — c )
p ( p — a )( p — b )( p — c ) p ( p — a )( p — b )( p — c )
p = ( a + b + c ) / 2
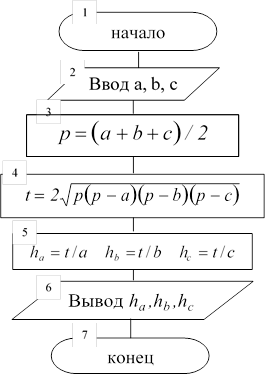
При решении данной задачи для исключения повторений следует вычислять высоты не по приведенным выше формулам непосредственно, а используя промежуточную переменную:
t = 2
p ( p — a )( p — b )( p — c ) ,
h a = t / a,
h b = t / b,
h c = t / c
Схема алгоритма решения задачи имеет следующий вид:
Для записи программы линейной структуры необходимы операторы присваивания, ввода исходных данных и вывода результатов вычислений.
Программа на языке Pascal состоит из заголовка, раздела описаний и раздела операторов:
раздел описаний begin
Существует определенный порядок в разделе описаний:
— раздел меток Label;
— раздел констант Const;
— раздел типов Type;
— раздел переменных Var;
— раздел процедур и функций (Function и Procedure).
Раздел операторов заключается в операторные скобки вида: Begin (начать) и End (закончить), при этом после End ставится точка. Точка – это признак окончания программы. В разделе операторов записывается последовательность выполняемых операторов. Операторы отделяются друг от друга символом » ; «
Оператор присваивания – это основной оператор любого языка программирования. Он предназначен для замены текущего значения переменной новым значением.
Форма оператора присваивания имеет вид:
Переменная : = выражение;
При выполнении этого оператора значение выражения вычисляется и присваивается переменной.
w := sin(sqr(t))/(s + ln(v)); s := „строка‟;
Имя переменной и результат выражения должны принадлежать к одному типу.
Для ввода данных используются операторы:
read (элемент 1, элемент 2, . );
readln (элемент 1, элемент 2, . );
При выполнении оператора read (элемент1, элемент2, . ) происходят следующие действия: программа приостанавливает свою работу и ждет, пока на клавиатуре будут набраны данные и нажата клавиша Enter. После нажатия клавиши Enter, введенные значения присваиваются переменным, имена которых указаны в операторе read. Числовые значения должны быть набраны в одной строке и разделены пробелами.
Оператор readln (элемент 1, элемент 2, . ) осуществляет ввод данных, а затем обеспечивает переход к началу новой строки.
Для вывода данных используются операторы:
write (элемент 1, элемент 2, . );
writeln (элемент 1, элемент 2, . );
где элемент – это переменная или строка символов, заключенная в апострофы.
write („ Значение В= „, В);
выводит на экран дисплея текст
а затем числовое значение переменной В.
Для вывода целых и действительных чисел можно указывать форматы в операторе WRITE. Формат указывается через двоеточие после переменной. Для действительных чисел формат состоит из двух величин. Первая величина указывает на общее количество позиций для вывода числового значения переменной: знак числа, количество цифр в целой части, точку и количество цифр в дробной части, второе – количество позиций для вывода дробной части. Например, оператор WRITE (Y:5:2) осуществит вывод значения Y на экран и при этом для отображения значения Y будет отведено пять позиций, из них две – на дробную часть.
Для вывода целых чисел количество позиций для дробной части не указывается. Например, если необходимо вывести значение целого
числа N=125, то оператор вывода будет иметь вид: WRITE (‘N=’, N:3), т.е. для вывода числового значения N отведено 3 позиции.
Допускается использование оператора вывода writeln (элемент1, элемент2 . ), который сначала выводит значения переменных, а затем осуществляет переход на новую строку.
Оператор writeln обеспечивает пропуск одной строки и переход к началу новой строки.
Текст программы решения задачи, схема которой приведена в примере имеет вид:
Var a,b,c,p,t,ha,hb,hc:real; Begin
Writeln(„vvod а ,b,c‟);
writeln („ha=‟,ha:6:2,‟ hb=‟,hb:6:2, „ hc=‟, hc:6:2); end.
Исходными данными для решения задачи являются значения длин сторон треугольника: a, b, c. Для ввода этих значений используется оператор Readln. В программе используется переменная p для вычисления полупериметра и вспомогательная переменная t для исключения повторений.
Вычисленные значения высот ha, hb, hc выводятся с соответствующими именами переменных. Когда выводятся элементы списка вывода, пробелы между ними не устанавливаются автоматически, поэтому необходимо непосредственно их указать в списке вывода. Для улучшения внешнего вида данных, которые выводятся на экран дисплея, используется форматированный вывод.
1. Изучить лекционный материал и методические рекомендации для выполнения задания.
2. Разработать алгоритм для расчета заданных переменных.
3. Составить программу на алгоритмическом языке Pascal.
4. Выполнить отладку и тестирование программы на компьютере.
5. Подготовить отчет о выполнении задания. Пример оформления отчета представлен в приложении 2.
6. Подготовить ответы на контрольные вопросы.
Варианты заданий
Источник: znanio.ru