Метрика – это мера, определяющая расстояние между элементами множества, которая обладает следующими свойствами:
1. Неотрицательна (>=0)
2. Нулевая при совпадении элементов
3. Симметрична (AB = BA)
4. Подчиняется закону треугольника (AB + BC > AC)
Метрика качества программ – система измерений качества программ. Эти измерения могут поводится на уровне критериев качества программ (сравнение программ по качеству) или на уровне отдельных характеристик качества.
В исследовании метрик выделяют два основных подхода:
1. Метрики оценки самого ПО (поиск метрик, характеризующих наиболее специфические свойства программ)
2. Метрики оценки технологии разработки ПО (оценка технических характеристик и факторов разработки программ)
По виду информации, получаемой при оценке качества ПО метрики можно разбить на три группы:
1. Метрики, оценивающие отклонение от нормы характеристик исходных проектных материалов (устанавливают полноту заданных технических характеристик исходного кода);
Как узнать родословную по фамилии | Метрические книги и ревизии | Генеалогия для начинающих
2. Метрики, позволяющие прогнозировать качество разрабатываемого ПО;
3. Метрики, по которым принимается решение о соответствии конечного ПО заданным требованиям.
В зависимости от характеристик и особенностей применяемых метрик им ставятся в соответствие различные измерительные шкалы:
1. Номинальной шкале соответствуют метрики, классифицирующие программы по признаку наличия или отсутствия какой-либо характеристики без учёта градации.
Например: программы можно группировать как «нетрудные для понимания», умеренно трудные для понимания», «трудные для понимания», «очень трудные для понимания».
2. Порядковой шкале соответствуют метрики, позволяющие ранжировать некоторые характеристики путем сравнения с опорными значениями, т.е.программы классифицируются по градации наличия какой-либо характеристики и упорядоченно располагаются по оси этой характеристики.
Например: некоторые программы А,В,С, относятся к разряду «умеренно трудных для понимания», но программа В труднее программы А, а программа А труднее программы С.
3. Метрики интервальной шкалы показывают не только относительное положение программ, но и то на сколько условных единиц отстоит одна программа от другой.
Например: можно сказать: программа В труднее программы А на 10 единиц.
4. Относительная шкала позволяет не только расположить программы определенным образом и оценить положение программ относительно друг друга, но и позволяют классифицировать их таким образом, что возможна сравнительная оценка других программ относительно базовой.
Например: можно сказать, программа В в два раза труднее программы А.
3. В настоящее время в мировой практике используется несколько сотен метрик программ. Существующие качественные оценки можно сгруппировать по 6 основным направлениям:
1. Оценка топологической и информационной сложности программ.
2. Оценка надёжности ПС, позволяющая прогнозировать отказы и отказовые ситуации.
#2 Как изучать метрические книги?
3. Оценка производительности ПО и повышения его эффективности путем выявления ошибок проектирования.
4. Оценка уровня языковых средств и их применения.
5. Оценка трудности восприятия и понимания программных текстов, ориентированная на психологические факторы, существенные для сопровождения и модификации программ.
6. Оценка производительности труда программиста для прогнозирования сроков и этапов разработки программ.
Метрики сложности программ
Поскольку проблема сложности программ включает широкий круг вопросов, начнем с рассмотрения основных направлений исследований в области оценки сложности программ, используя примеры метрических характеристик, применяемых на практике.
При оценке сложности выделяют 3 группы метрик: 1. Метрики размера.2. Метрики сложности потоков управления программы. 3.Метрики сложности потоков данных программы.
1. Оценки первой группы наиболее просты и потому получили более широкое применение. Традиционной характеристикой размера программ является количество строк исходного текста. (Под строкой понимается любой оператор программы, поскольку реально при оценке размера программ используется информация именно о количестве операторов).
Непосредственное измерение размера программы, несмотря на свою простоту, дает хорошие результаты. Ее недостаточно для принятия решения о сложности, но она вполне применима для классификации программ, различающихся по объему.
Т.о., оценка размера программы – оценка по номинальной шкале.
К группе оценок размера программ можно отнести метрику Холстеда. За базу принят подсчет количества операторов и операндов, используемых в программе., т.е. также определение размера программы.
Основу метрики Холстеда составляют четыре измеряемые характеристики программы:
η1 – число уникальных, различных операторов программы, включая символы-разделители, знаки операций, имена процедур и функций (словарь операций).
η2 – число уникальных, различных операндов программы (словарь операндов).
N1 – общее количество операторов в программе.
N2 – общее количество операндов в программе.
Опираясь на эти характеристики, получаемые непосредственно при анализе исходных текстов программ, М.Холстед вводит следующие оценки:
словарь программы η = η1 + η2 (1)
объем программы V = Nlog2 η (3)
Далее М.Холстед вводит η * — теоретический словарь программы, т.е.словарный запас, необходимый для написания программы с учетом того, что необходимая функция уже реализована в данном языке и, следовательно, программа сводится к вызову этой функции.
Например: согласно М.Холстеду, возможное осуществление процедуры выделения простого числа могло бы выглядеть так:
где Y- массив численных значений, содержащих искомое число X.
Теоретический словарь в данном случае будет состоять из
Используя η * , Холстед вводит характеристику V * :
V * = η * log2 η * , (5)
с помощью которой описывается потенциальный объем программы, соответствующий максимально компактному тексту программы, реализующей данный алгоритм.
Задание:
Для одной из своих программ рассчитать:
1) Реальную длину программы, (N).
2) Теоретическую длину программы, (η * )
3) Реальный объем программы, (V)
4) Потенциальный объем программы(V * ).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Перечислите наиболее известные методы оценки метрических характеристик качества программных продуктов.
2. Перечислите основные требования к критериям качества ПО.
3. Перечислите разновидности метрик, шкал. Поясните принципы двух основных подходов в исследовании метрик.
4. Как с помощью метрик сложности программ определить длину и объём программы?
ЛИТЕРАТУРА
1. Липаев В.В. Качество программного обеспечения. – М.: Финансы и статистика, 1983.
2. Холстед М. Начала науки программирования. — М.: Финансы и статистика, 1981.
Лабораторная работа №6
Источник: infopedia.su
Организационно-экономический раздел. Программометрика.
Метрическая теория программ — программометрика — это научное и прикладное направление, возникшее в информатике около 30 лет назад. Программометрика позволяет решать следующие задачи:
· количественный анализ возможности и целесообразности разработки автоматизированных процедур и функций информационных систем (ИС) в заданной постановке;
· численная оценка основных параметров (объем, количество модулей, уровней иерархии, надежность в начальный период эксплуатации) будущих программных средств (ПС) на основе постановки задачи;
· планирование и управление разработкой ПС, оценка трудоемкости его создания, технико-экономическое обоснование;
· решение некоторых вопросов, связанных с метрологией качества ПС.
Наиболее разработанной и проверенной на практике является объемная метрика Холстеда. Холстед теоретически получил соотношение, связывающее размер словаря программы h и ее длину N:
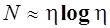
(4.1)
Дальнейший расчет метрических характеристик производится по метрике Холстеда, изложенной в [1].
4.2. Основные метрические характеристики
h — число слов в словаре программы. Словарь программы состоит из h1 операторов и h2 операндов. Размер словаря программы h = h1 + h2. К словарю операторов относят имена арифметических и логических операций, присваивания, условных и безусловных переходов, разделители, скобки, имена процедур и функций и т.п. Словарь операндов — это множество имен переменных, которое должно обрабатывать проектируемое ПС.
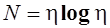— длина программы. Это математическое ожидание количества слов в тексте программы при фиксированном словаре. Длина программы — исходная величина для расчета остальных метрических характеристик программы. Т.к. h = h1 + h2, то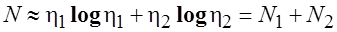 
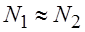, тогда
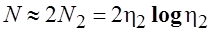
(4.2)
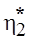
— количество имен входных и выходных переменных, представленных в предельно краткой записи. Это основной исходный параметр, на котором базируются все расчеты метрических характеристик будущего ПС. Тогда в соответствии с соотношением (4.1)
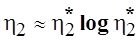
(4.3)
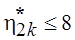
k — число модулей. Наименьшее количество ошибок обнаруживается в модулях с числом входных переменных . Тогда оптимальное число модулей ПС находим по формуле:
(4.4)
В этом случае число входных переменных одного модуля . Тогда выражение для длины программы будет иметь вид:
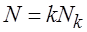
, (4.5)
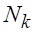
где — длина одного модуля, найденная по формуле (4.2).
V — объем программы. Измеряется числом двоичных разрядов.
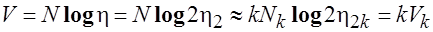
(4.6)
Календарное время программирования определяется по формуле:
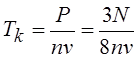
(4.7)
где n — количество программистов,
v — заданная производительность труда, которая составляет от 5 до 30 отлаженных команд ассемблера за рабочий день,
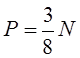
— количество команд ассемблера в ПС из N слов.
Начальное количество ошибок (перед комплексной отладкой):
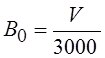
(4.8)
Надежность ПС оценивается средним временем проявления ошибок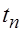 
. 
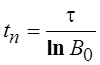(4.9)
где t — период отладки в пределах календарного времени разработки. Исходя из практического опыта, его определяют из неравенства
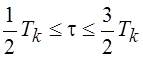
(4.10)
4.3. Расчет метрических характеристик
4.3.1 Рассматриваемые процедуры
Translate — анализа строки запроса;
Select — передача запроса в базу данных и обработка полученных результатов;
Value — определение типа значения, содержащегося в строке;
Equal — эквивалентность нечетких значений;
DeleteFuzzyObjectList — удаляет требуемый элемент из списка нечетких объектов базы данных.
4.3.2 Пример расчет метрических характеристик
Процедура Translate.
Входные параметры:
1. Анализируемая строка запроса
Выходные параметры:
2. Модифицированная строка запроса
3. Список нечетких условий
4. Индекс типа запроса
Структурные параметры ПС:
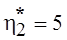
Количество имен входных и выходных переменных
Источник: vunivere.ru
Метрические характеристики программ. Словарь программы
2.4.1. Один из наиболее важных количественных показателей — это длина программы N, нами уже получен. Он представляет собой математическое ожидание количества слов в тексте программы при фиксированном словаре. Ясно, что программы, реализующие один и тот же алгоритм, написанные разными программистами, будут несколько различаться по длине. Фундаментальное значение формулы Холстеда заключается в том, что это различие с ростом словаря программы весьма быстро уменьшается, как показано выше.
Длина программы — это исходная величина для расчета остальных ее характеристик.
2.4.2. Другая важная характеристика программы — ее объем V. В отличие от N он измеряется не количеством слов, а числом двоичных разрядов. Если в словаре имеется г слов, то для задания номера любого из них требуется минимум logp бит. Объем программы определяется как
Теперь, когда получены две расчетные метрические характеристики программ, имеет смысл вернуться к пункту 2.1. Если алфавиту поставить в соответствие словарь, а произвольной последовательности символов — последовательность слов в программе, трактуемой как результат выборки из генеральной совокупности, то с точностью до обозначений полученные соотношения
совершенно идентичны, хотя смысл их различен. В первом случае при фиксированной (заданной) длине программы была определена величина словаря; во втором — решена обратная задача: по заданному словарю найдена длина программы. Идентичность этих выражений свидетельствует о том, что соотношение между величиной словаря и длиной текста единственно и взаимнооднозначно. Во-вторых, вероятностная модель текста программы, основанная на наглядном представлении выборки из генеральной совокупности с возвратом, равносильна формальному подходу алгоритмической теории сложности.
Выше было отмечено, что словарь программы состоит только из операторов и операндов. Если количество первых обозначить а вторых — г|2, то Л = т 11 +Г 12 и соотношение Холстеда примет вид
При статистическом исследовании текстов программ [4] к словарю операторов отнесены: имена арифметических и логических операций; присваивания; условных и безусловных переходов; разделители; скобки; имена процедур и функций и т. п. Выражения типа BEGIN. END, IF. THEN. ELSE, DO. WHILE и другие рассматриваются как единые операторы (то же относится и к парам скобок).
Ясно, что величины Ц] и г2 независимы и могут принимать произвольные значения. Однако этого нельзя сказать относительно N и N2, т. е. числа всех операторов N = Ц] log г| и всех операндов N2=r2ogr2 в тексте программы: между ними существует зависимость, характер и вид которой определяются уровнем используемого алгоритмического языка. В случае машинного кода или ассемблера каждый операнд входит в текст программы, как правило, с одним оператором. Поэтому Ni=N2, хотя величины словарей и г2 могут сильно различаться. Это позволяет прийти к важному практическому заключению:
упрощающему все программометрические расчеты. Размер словаря операндов г2» как показано в п. 2.4.3, легко определяется из постановок задач. Для алгоритмического языка высокого уровня это соотношение нарушается, так как один оператор может применяться к нескольким операндам (см. п. 2.7.3).
Теперь для вычисления объема, в соответствии с его определением, получим
2.4.3. Основной исходный параметр, на котором базируются все расчеты ожидаемых метрических характеристик будущего ПО, — это
количество имен входных и выходных переменных г2, представленных в предельно краткой (сжатой, с точки зрения алгоритмической сложности) записи. Например, для задания одномерного массива (строки), каково бы ни было число его элементов, требуется всего три имени: а) указатель адреса начала массива, б) количество элементов в нем, в) адрес конца массива (или количество разрядов, занимаемых одним элементом). Для задания двумерного массива достаточно пяти имен. Этот подход к представлению входной и выходной информации обеспечивает компактность и инвариантность программ относительно
размерности решаемых задач.
Пусть ц 2 — число независимых переменных произвольной функции |/, заданной формулой или алгоритмом вычисления.
Понятно, что в программе ее вычисления на ассемблере (или близком к нему машинном коде) фактическое количество операндов будет больше. Дело в том, что аналитическая запись р может в общем случае представлять собой суперпозицию функций меньшего числа тех же аргументов, каждой из которых должно быть присвоено уникальное имя (в случае алгоритма — промежуточным результатам вычислений). Используя отмеченные выше свойства текстов программ, можно показать, что численное значение величины полного (фактического) словаря операндов при использовании языков подобного уровня будет
ц 21°ё Л2 • Если, например, — функция Буля восьми
переменных, то т2 =8, аг|2 =81^8 = 24. Для одномерного массива
- *
- (строки) г)2 =3, соответственно г|2 = 3 к^3»5. Разумеется, речь идет о рационализированных («максимально сжатых» формулах, лишенных
избыточности или, по Холстеду, «несовершенств» [4]).
Таким образом, если г2 — размер словаря программы в предельно краткой записи, то его полное значение будет
Способ представления входных данных — одна из главных задач разработки ПО, и удачное ее решение относится к числу «стратегических находок» проекта [1]. На примере представления массивов видно, как длина программы становится независимой от количества элементов в них. По существу, это эффективный способ сокращения размера словаря, от которого зависят и другие характеристики программы.
2.4.4. Рассмотрим некоторый абстрактный язык программирования, называемый потенциальным, в котором все программы (по крайней мере для некоторой предметной области) уже написаны и представлены в виде процедур или функций. Тогда для реализации любого алгоритма на этом языке потребуется всего два оператора (функция и присваивание) и ц2 имен входных и выходных переменных. Поскольку в такой записи никакие слова не повторяются, то длина программы совпадает с ее объемом и равна
Эта величина называется потенциальным (минимально возможным) объемом, а отношение
— уровнем реализации программы. Данный метрический показатель характеризует степень компактности программы, экономичность использования изобразительных средств алгоритмического языка. Чем ближе значение I к единице, тем совершеннее программа.
Источник: studref.com