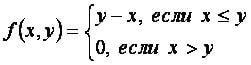Что представляет собой программа для машины тьюринга

Машина Тьюринга представляет собой (абстрактное) устройство, состоящее из ленты, управляющего устройства и считывающей головки.

Лента разбита на ячейки. Во всякой ячейке в точности один символ из внешнего алфавита A=0,a1. an>. Некоторый символ (будем обозначать его Λ) алфавита A называется пустым, а любая ячейка, содержащая в данный момент пустой символ, называется пустой ячейкой (в этот момент). Лента предполагается потенциально неограниченной в обе стороны.

Управляющее устройство в каждый момент времени находится в некотором состоянии qj, принадлежащем множеству Q=0,q1. qm> (m=l). Множество Q называется внутренним алфавитом. Одно из таких состояний (обычно q0) называется заключительным, а некоторое другое (обычно q1) -начальным.

Считывающая головка перемещается вдоль ленты так, что в каждый момент времени она обозревает ровно одну ячейку ленты. Головка может считывать содержимое обозреваемой ячейки и записывать в нее вместо обозреваемого символа некоторый новый символ из внешнего алфавита A (возможно тот же самый).

Что такое и как устроена машина Тьюринга? Душкин объяснит

В процессе работы управляющее устройство в зависимости от состояния, в котором оно находится и символа, обозреваемого головкой, изменяет свое внутреннее состояние q. Затем выдает головке приказ напечатать в обозреваемой ячейке определенный символ из внешнего алфавита A, а потом приказывает головке либо остаться на месте, либо сдвинуться на одну ячейку вправо, либо сдвинуться на одну ячейку влево. Попав в заключительное состояние, машина прекращает работу.

Конфигурацией на ленте (или машинным словом) называется совокупность, образованная:

1) последовательностью ai(1),ai(2). ai(s) символов из внешнего алфавита А, записанных в ячейках ленты, где ai(1) — символ записанный в первой ячейке слева и т.д. (любая такая последовательность называется словом)

2) состоянием внутренней памяти qr

3) номером k воспринимаемой ячейки

Конфигурацию машины будем записывать так:

здесь r-воспринимаемая ячейка, выделяется в виде дроби.

Если машина, находясь во внутреннем состоянии qi, воспринимает ячейку с символом au, записывает к следующему моменту времени в эту ячейку символ ar, переходит во внутреннее состояние qs и сдвигается по ленте, то говорят, что машина выполняет команду qiau→qsarS, где символ S может принять одно из значений: -1 — сдвиг головки влево; +1 — сдвиг головки вправо; 0 — головка остается на месте. Список всех команд (пятерок), определяющих работу машины Тьюринга, называется программой этой машины. Программу машины часто задают в виде таблицы. Так для описанной выше ситуации в таблице на пересечении строки ai и столбца qi будет стоять qsarS.

q0	.	qi	.	qm
.
au	qsarS
.

Если в программе машины для пары (qi,au) пятерка отсутствует, то в таблице на пересечении строки au, и столбца qi ставится прочерк.

Машина Тьюринга. Введение. Понятие машины тьюринга. Решение задачи

Итак, машина Тьюринга есть, по определению, набор М=(А,Q,П), где А — внешний алфавит, Q — алфавит внутренних состояний, П — программа.

Если машина, начав работу с некоторым словом P, записанным на ленте, придет в заключительное состояние, то она называется применимой к этому слову. Результатом ее работы считается слово, записанное на ленте в заключительном состоянии. В противном случае, машина называется не применимой к слову Р.

Пример. Построим машину Тьюринга, складывающую натуральные числа, записанные в унарной системе счисления (т.е. записанные при помощи одного символа |. Например 5=|||||.).

Решение. Рассмотрим алфавит А = <|, +, Λ>.

Машина определяется следующей программой:

q1	q2	q3
|	|q1+1	Λq3-1	|q3-1
+	|q1+1
Λ	Λq2-1	Λq0+1

Выпишем последовательно возникающие при работе этой машины конфигурации на исходном слове ||+|||, т.е. 2+3. Здесь при записи конфигурации будем использовать следующее соглашение: состояние, в котором находится машина, записывается в круглых скобках справа за обозреваемой буквой.

Пример. Построить машину Тьюринга, удваивающую натуральные числа, записанные в унарной системе счисления.

Решение. Искомую машину построим в алфавите A=<|, α, Λ>.

Программа такой машины может выглядеть так:

q1	q2	q3
|	αq1+1	|q2-1	|q3+1
α	|q3+1
Λ	Λq2-1	Λq0+1	|q2-1

Применим полученную машину к слову ||.

Введение новой буквы α и замена исходных | на α позволяет различить исходные | и новые (приписанные) |. Состояние q1 обеспечивает замену | на α, состояние q2 обеспечивает поиск α, предназначенных для замены на |, и останов машины в случае, когда α не обнаружено, q3 обеспечивает дописывание | в случае, когда произошла замена α на |.

Источник: tablica-istinnosti.ru

Что собой представляет машина Тьюринга?

Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (каретки), которая управляется программой. Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.

Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:

• Внешний алфавит.Конечное множество (например, А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а0) должна представлять собой пустой символ.
• Внутренний алфавит.Конечное множество состояний каретки (автомата). Одно из состояний (например, q1) должно быть начальным (запускающим программу). Еще одно из состояний (q0) должно быть конечным (завершающим программу) – состояние останова.
• Таблица переходов.Описание поведения автомата (каретки) в зависимости от состояния и считанного символа.

• Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).
• Передвигаться на одну ячейку влево или вправо.
• Менять свое внутреннее состояние.

Пример работы машины Тьюринга

Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова. 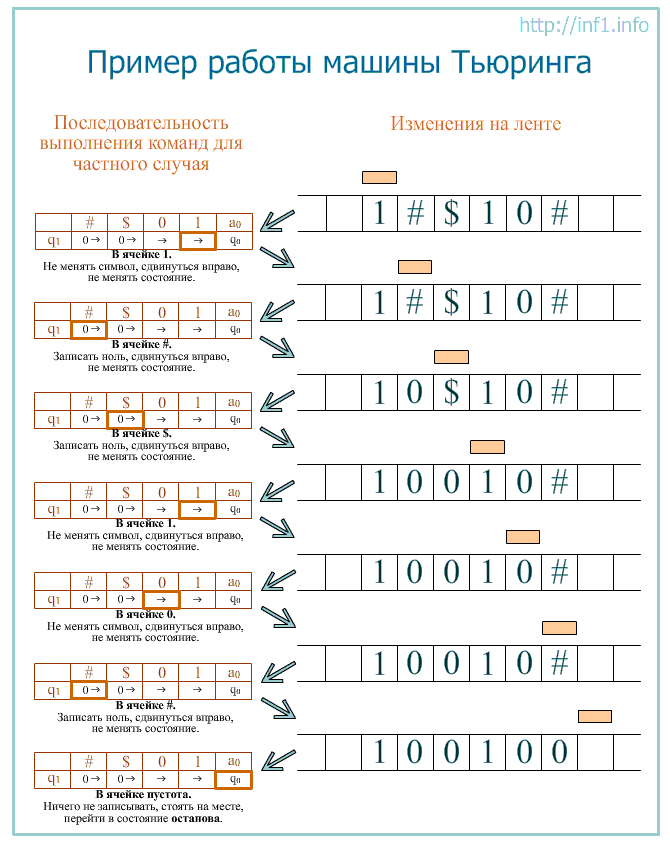Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой): Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние q2 (команды которого совпадают с командами q1 предыдущей программы).

1. Современная теория алгоритмов

Начальной точкой отсчета современной теории алгоритмов можно считать теорему о неполноте символических логик, доказанную немецким математиком Куртом Геделем в 1931 г. В этой работе было показано, что некоторые математические проблемы не могут быть решены алгоритмами определенного класса. Общность результата Геделя связана с вопросом о том, совпадает ли использованный им класс алгоритмов с классом всех алгоритмов в интуитивном понимании этого термина. Эта работа дала толчок к поиску и анализу различных формализаций понятия алгоритм. Первые фундаментальные работы по теории алгоритмов были опубликованы в середине 1930-х гг. Аланом Тьюрингом, Алоизом Черчем и Эмилем Постом. Предложенные ими машина Тьюринга, машина Поста и класс рекурсивно-вычислимых функций Черча были первыми формальными описаниями алгоритма, опирающимися на строго определенные модели вычислений. Сформулированные гипотезы Поста и Черча-Тьюринга постулировали эквивалентность предложенных ими моделей вычислений, как формальных систем, и интуитивного понятия алгоритма. Важным развитием этих работ стала формулировка и доказательство существования алгоритмически неразрешимых проблем. В 1950-х гг. существенный вклад в развитие теории алгоритмов внесли работы Колмогорова и основанный на теории формальных грамматик алгоритмический формализм Маркова – так называемые нормальные алгоритмы Маркова. Формальные модели алгоритмов Поста, Тьюринга и Черча, равно как и модели Колмогорова и Маркова, оказались эквивалентными в том смысле, что любой класс проблем, разрешимых в одной модели, разрешим и в другой. Появление доступных ЭВМ и существенное расширение круга решаемых на них задач привели в 1960-1970-х гг. к практически значимым исследованиям алгоритмов и вычислительных задач. На этой основе впоследствии выделилось несколько разделов теории алгоритмов.

Источник: studfile.net

Машина Тьюринга

Машина Тьюринга (МТ) — абстрактная вычислительная машина для выполнения программ, предложенная английским математиком Аланом Мэтисоном Тьюрингом в 1936 году.

Ниже описана детерминированная машина Тьюринга. Есть её обобщения — см. вероятностная машина Тьюринга (а также недетерминированная машина Тьюринга).

• 1 Состав МТ
• 2 Виды команд:
• 3 Виды командных строк:
• 4 Пример задачи

• 4.1 Программа для МТ
• 4.2 Таблица для программы

• 5.1 Пример 1
• 5.2 Пример 2

Состав МТ

МТ состоит из управляющего устройства (каретки или считывающей и записывающей головки) и ленты, разбитой на секции (ячейки) и бесконечной в обе стороны. В каждой ячейке ленты может быть какой-либо символ конечного алфавита, включающего пробел.

За один шаг каретка может считать и записать символ алфавита в том месте, где она стоит и сдвинуться на одну позицию влево или вправо или остаться на месте. Управляющее устройство может находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство работает согласно правилам перехода (командным строкам), которые представляют алгоритм (программу). Конкретная программа для МТ задаётся перечислением элементов множества букв алфавита, множества состояний и набором правил, по которым работает МТ. Для каждой возможной конфигурации имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Работа МТ определяется программой, состоящей из конечного числа командных строк.

Виды команд:

• сдвиг вправо
• сдвиг влево
• остаться на месте
• запись символа алфавита в ячейку
• перейти в состояние из множества

n — число состояний управляющего устройства без конечного;

Q=0, q1, q2, …, qn> — множество состояний управляющего устройства с конечным состоянием (q0);

k — число символов алфавита;

s1 — номер состояния, в котором управляющее устройство находится до выполнения команды;

s2 — номер состояния, в которое управляющее устройство переходит после выполнения команды;

a1 — считываемый символ a1;

a2 — записываемый символ a2;

R — сдвиг вправо;

L — сдвиг влево;

M — оставание на месте.

Виды командных строк:

s1a1s2a2M — при считывании символа a1 в состоянии s1 записать символ a2, перейти в состояние s2 и остаться на месте;

s1a1s2a2R — при считывании символа a1 в состоянии s1 записать символ a2, перейти в состояние s2 и осуществить сдвиг каретки вправо на 1 ячейку;

s1a1s2a2L — при считывании символа a1 в состоянии s1 записать символ a2, перейти в состояние s2 и осуществить сдвиг каретки влево на 1 ячейку.

Для работы машины Тьюринга нужно задать программу и её начальное состояние (т. е. состояние управляющей системы, состояние ленты и позицию каретки). Предполагается, что неопределённая часть ленты заполнена символами пробела, т.е. она чистая.

После запуска программы на МТ возможны следующие варианты:

• работа может закончиться если система переходит в терминальное (конечное) состояние;
• работа никогда не закончится (т.е.программа составлена не корректно).

Пример задачи

, где x, y — неотрицательные целые числа.

Программа для МТ

Таблица для программы

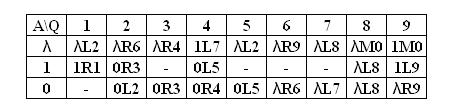
Примеры работы МТ:

1 — число 0;

11 — число 1;

111 — число 2;

1 x+1 — неотрицательное целое число x;

1 y+1 — неотрицательное целое число y;

1 x+1 λ1 y+1 — набор значений аргументов (x,y).

Пример 1

Входные данные: 111λ1.

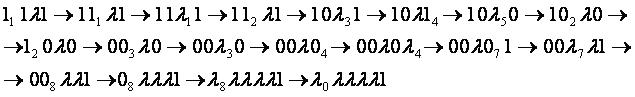
Выходные данные: λ0λλλλ1.

Пример 2

Входные данные: 11λ111.

Выходные данные: λ1011.

• Заметим, что машина Поста во многом аналогична машине Тьюринга.

Обобщения

Недетерминированная машина Тьюринга — обобщение детерминированной машины Тьюринга, в которой при каждом переходе можно выполнять переход одновременно в несколько (константа) состояний — можно считать, что происходит «клонирование» машины (состояние, содержимое лент, положение головок). Таким образом, для каждого массива входных данных имеется не один, а несколько (в общем случае — экспоненциальное число) путей, по которым может развиваться вычисление.

Недетерминированная машина Тьюринга выдаст ответ 1, если существует хотя бы один путь развития вычисления, на котором выдается ответ 1, и 0 — в противном случае (таким образом, ответы «ДА» и «НЕТ» в случае недетерминированных вычислений несимметричны).

Вероятностная машина Тьюринга — обобщение детерминированной машины Тьюринга, в которой из любого состояния и значений на ленте, машина может совершить один из нескольких (можно считать, без ограничения общности — двух) возможных переходов, а выбор осуществляется вероятностным образом (подбрасыванием монетки).

Вероятностная Машина Тьюринга похожа на недетерминированную машину Тьюринга, только вместо недетерминированного перехода, машина выбирает один из вариантов с некоторой вероятностью.

Другие алгоритмы

• наибольший общий делитель;
• наименьшее общее кратное;
• проверка кратности;
• деление по модулю;
• решето Эратосфена;
• разложение числа на множители;
• система счисления;
• метод математической индукции;
• схема примитивной рекурсии;
• виды рекурсии;
• машина Поста;
• машина Тьюринга (вероятностная);
• комбинаторные алгоритмы;
• сортировка;
• алгоритм определения мест.

Ссылки

• Участник:Logic-samara
• Машина Тьюринга в Абсурдопедии на Викии (юмористическая статья)

Источник: cyclowiki.org