Что называется невозможной фигурой в программе autocad

Невозможные фигуры — особый вид объектов в изобразительном искусстве. Как правило их называют так, потому что они не могут существовать в реальном мире. Драконы, эльфы, гномы также не могут существовать в реальном мире, но они не являются невозможными фигурами.

Более точно, невозможными фигурами называют геометрические объекты, нарисованные на бумаге, которые прозводят впечатление обычной проекции трехмерного объекта, однако, при внимательном рассмотрении становятся видны противоречия в соединениях элементов фигуры.

Таким образом, на изображении ниже мы видим лишь одну невозможную фигуру — невозможный треугольник. Инопланетное существо, которое держит треугольник, к невозможным фигурам не относится.

Невозможные фигуры выделяют в отдельный класс оптических иллюзий.

Невозможные конструкции известны с давних времен. Они встречаются в иконах со средних веков. «Отцом» невозможных фигур считается шведский художник Оскар Реутерсвард, который нарисовал невозможный треугольник, составленный из кубиков в 1934 году. За годы творчества он придумал и нарисовал несколько тысяч невозможных фигур.

Если не отображается Модель — Лист в Autocad

Известны широкой публике невозможные фигуры стали в 50-х годах прошлого века, после публикации статьи Роджера Пенроуза и Лайонела Пенроуза в Британском журнале психологии, в которой были описаны две базовые фигуры — невозможный треугольник (который также называют треугольником Пенроуза) и бесконечная лестница. Эта статья попала в руки известного голландского художника М.К.

Эшера, который вдохновленный идеей невозможных фигур создал свои знаменитые литографии «Водопад», «Восхождение и спуск» и «Бельведер». Вслед за ним огромное количество художников по всему миру стали использовать невозможные фигуры в своем творчестве. Наиболее известны среди них Жос де Мей, Сандро дель Пре, Оштван Орос. Работы этих, а также других художников, выделяют в отдельное направление изобразительного искусства — «имп-арт», от английских слов impossible («невозможный») и art («искусство»).

Может показаться, что невозможные фигуры действительно не могут существовать в трехмерном пространстве. Есть определенные способы, которые позволяют воспроизвести невозможные фигуры в реальном мире, правда они будут выглядет невозможными только с одной точки обзора. С других точек обзора видны искажения и разрывы в фигуре.

1. Какие возможности предоставляет программа AutoCAD (Несколько вариантов ответа):
*создание рисунков деталей
*создание выкройки изделия
*презентация готового изделия

2. Целью изучения программы AutoCAD является (несколько ответов):
*умение и применение чтения чертежей, технических рисунков, схем изделий
*применение навыков шитья
*развитие эстетического вкуса

3. Какие тренировочные графические задания можно выполнить, используя AutoCAD(несколько вариантов ответа):

Определяем сумму длин выделенных отрезков в Autocad

*развлекательные задачи
*занимательные задачи
*творческие задачи
*логические задачи

4. Программа AutoCAD развивает у учеников (несколько вариантов ответа):
*умение выполнять самостоятельно творческие работы
*умение правильно выбирать курс обучения
*умение оценивать свою работу с разных сторон

5. Требования к графической компетенции учеников (несколько вариантов ответа):
*знать разные виды конструкторов
*знать детали и конструктивные элементы
*знать изделия и сборочные единицы

6. Системы координат используемые в AutoCAD (несколько вариантов ответа):
*D
*X
*Y
*Z

7. Для каких целей нужна система AutoCAD:
*для игр
*для построения чертежей и 2D И 3D изображений
*для проверки на вирусы
*для рисования
*редактирования текста

8. К графическим документам 2D относят:
*спецификация
*деталь
*фрагмент
*чертеж
*документ

9. 3D моделирование это:
*получение плоского чертежа
*получение детали в трех проекциях
*получение пространственного объект а

10. Какая компания разработала систему AutoCAD:
*САПР
*IronCAD
*Autodesk

11. Есть ли в системе AutoCAD редактор текста:
*да
*нет
*в зависимости от версии AutoCAD

12. С чего начинается выпуск модели (несколько вариантов ответа):
*идеи
*оплаты
*схемы
*фотографии

13. В каких областях можно применять 3D модель AutoCAD (неколько вариантов ответа):
*дизайн
*геология
*инженерно-технические
*геодезия
*военных

14. Способы масштабирования в AutoCAD (несколько вариантов ответа):
*колесиком мыши
*базовая точка
*по отрезку

15. Что такое зуммирование в программе AutoCAD (несколько вариантов ответа):
*планирование объекта
*приближение объекта
*вид объекта
*отдаление объекта

16. Каким цветом подсвечиваются выделенные объекты по умолчанию в системе AutoCAD (несколько вариантов ответа):
*филетовый
*оранжевый
*синий
*зеленый

17. Что называют невозможной фигурой:
*пирамида
*трезубец
*конус
*призма
*треугольник

18. Какая плоскость в AutoCAD отвечает за вид детали справа и слева (несколько вариантов ответа):
*XY
*XZ
*ZY
*YY

19. Для чего нужен графический редактор:
*управлять компьютером при помощи рисунков
*для получения и обработки изображения деталей
*для работы с текстом

20. AutoCAD относится к . редактору
*фронтальному
*текстововму
*растровому
*векторному
*гибридному

ФИГУРА, НЕВОЗМОЖНАЯ — Любая из класса фигур, в которых отдельные компоненты вызывают противоречивые интерпретации. В примере, приведенном здесь, правая сторона имеет сигналы для оценки объекта как двузубчатого, нолевая – как трехзубчатого. Таким образом, такой предмет … Толковый словарь по психологии

Лестница Пенроуза — (бесконечная лестница, невозможная лестница) это одна из основных невозможных фигур, открытая Оскаро … Википедия

Перспектива — У этого термина существуют и другие значения, см. Перспектива (значения). Пример перспективы в фотографии. «Блошиный рынок в Москве, вид с моста до станции … Википедия

Список парадоксов — … Википедия

Парадоксы — Служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавливается на информационные статьи списки и глоссари … Википедия

Натюрморт и улица — Эшер, Мауриц Корнелис Натюрморт и улица, 1937 англ. Still Life and Street Ксилография. 48,7×49 см «Натюрморт и улица» ксилография нидерландского художника Эшера, впервые напечатанная в марте 1937 года, и хранящаяся в коллекции… … Википедия

Словарь терминов шахматной композиции — # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С Т У Ф Х Ц … Википедия

Анна Каренина — У этого термина существуют и другие значения, см. Анна Каренина (значения). Анна Каренина … Википедия

Джоконда — Леонардо да Винчи Мона Лиза, 1503 1505 Ritratto di Monna Lisa del Giocondo Дерево, масло. 76,8 × 53 см Лувр, Париж «Мона Лиза» (итал … Википедия

Мадонна Лиза — Леонардо да Винчи Мона Лиза, 1503 1505 Ritratto di Monna Lisa del Giocondo Дерево, масло. 76,8 × 53 см Лувр, Париж «Мона Лиза» (итал … Википедия

Источник: prokompter.ru

Сложные Объекты AutoCAD

К сложным объектам AutoCAD можно отнести фигуры, имеющие несколько усложненный способ построения или дополнительные средства по редактированию и настройке. Вообще, точное определение, выражающее кардинальное отличие сложных объектов от простых, сформулировать сложно. Условно можно отнести к сложным объектам следующие фигуры:

• мультилинии;
• области;
• полилинии;
• блоки и внешние ссылки;
• размерные блоки;
• многострочный текст.

МУЛЬТИЛИНИИ

Мультилинией в AutoCAD называется набор параллельных линий, вычерчивающихся одновременно. В наборе мультилинии может быть от 1 до 16 простых линий, которые могут иметь отличные друг от друга свойства (стиль, цвет и др.). Такие линии применяются для вычерчивания контуров стен, состоящих из оси, внутренней и внешней границ. Пример мультилинии приведен на рис. 1.26.

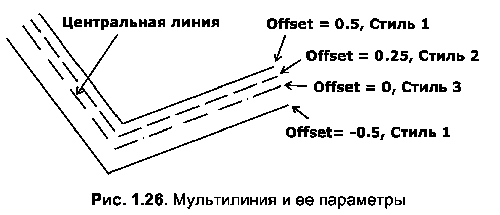
Каждая из одиночных линий мультилинии имеет свои собственные параметры. Наряду с опциями каждой линии имеются также параметры и у самой мультилинии. Основные из них: количество одиночных линий, их привязка к центральной оси тип окончания мультилинии, заливка.

Выбор для мультилинии определенного стиля или других опций осуществляется непосредственно при ее создании с помощью параметров команды Mline. По умолчанию стиль вычерчивания будет такой же, как и для последней построенной мультилинии.

Разновидностью линии является полилиния — последовательность отрезков и дуг, обрабатываемая как единое целое (например при редактировании или удалении). Полилиния – это один из немногих объектов AutoCAD, который может иметь ненулевую ширину. Кроме того, ширина начала полилинии может отличаться от ширины ее конца, и AutoCAD в таком случае плавно сопрягает их между собой.

Для создания полилинии служит команда Pline. При вводе этой команды AutoCAD сначала запрашивает координаты первой точки первого сегмента, далее – тип первого сегмента (линия или дуга), а также его ширину в точках начала и конца. Затем достаточно будет указать координаты второй точки первого сегмента (точки его конца). После построения первого сегмента цикл повторяется заново.

Так, например, на рис. 1.27 показаны две полилинии с одинаковыми типами сегментов (сегмент 1 и сегмент 2) и координатами их граничных точек (точка 1, точка 2, точка 3), но разной шириной в точках конца каждого сегмента (точка 2 в сегменте 1, точка 3 в сегменте 2).

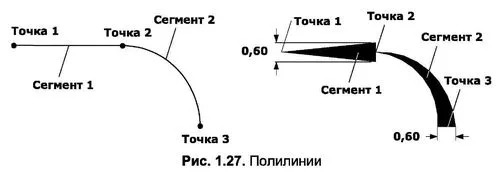
Примечание. При вычерчивании сегментов-дуг полилиний кривизна дуги может задаваться щелчком правой кнопки мыши в графической зоне или с использованием специального параметра центрального угла команды Pline.

После вычерчивания полилинии остается возможность ее последующего редактирования. Для этого предназначены граничные маркеры каждого из сегментов и маркеры кривизны сегментов с типом «дута». Подробнее параметры полилиний и работа с ними рассмотрены в главе 6 «Сложные объекты».

Также необходимо отметить, что в системе AutoCAD 2010 имеется команда, предназначенная для вычерчивания полилинии, имеющей форму облака. Речь идет о команде Revcloud, которую также можно выполнить нажатием кнопки Revcloud (Облака), расположенной в инструментальной группе Draw (Рисование) вкладкиНоте (Главная).

РАЗМЕРНЫЕ БЛОКИ

Размерные блоки — это особые объекты AutoCAD, предназначенные для оснащения чертежа видимой информацией о геометрических размерах, допусках и другими элементами точного представления технических данных. Процесс нанесения размерных блоков на объект можно назвать образмериванием, а сам объект – образмеренным. Любой размерный элемент AutoCAD настраивается в соответствии с требованиями ГОСТов.

Размерные блоки состоят (в зависимости от их типа) из нескольких элементов. Так, например, одинарный размерный блок (рис. 1.28) состоит из четырех элементов. Кроме того, для точной привязки размерного блока к фигуре, размер которой выносится в блоке, в AutoCAD используются элементы объектной привязки.

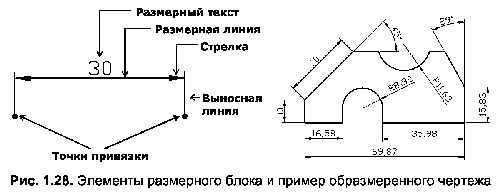
Примечание. Размеры, проставляемые AutoCAD, поддерживают с объектом ассоциативность, т.е. с изменением геометрических размеров или других характеристик объекта проставленные размеры соответствующим образом изменяются вместе с ними.

Для работы с размерными блоками в AutoCAD предназначена специальная панель инструментов Dimension (Размеры) и диалоговое окно Dimension Style Manager (Менеджерразмерных стилей).

Вопросы образмеривания в AutoCAD находят весьма широкое практическое применение – это очень мощный инструмент, заслуживающий по праву особого внимания пользователей. Подробнее об образмеривании рассказано в главе 6 «Сложные объекты».

Областями в AutoCAD называются объекты, образованные путем соединения в замкнутый контур нескольких простых фигур. Кроме того, в области можно преобразовывать круги, эллипсы и замкнутые полилинии.

Полезной особенностью областей является то, что AutoCAD может вычислить для них множество простых и сложных геометрических характеристик, таких как: площадь; периметр; центр тяжести; осевые, главные, полярные и центробежные моменты инерции и другие характеристики. Кроме того, область можно будет в дальнейшем заполнить однотонным цветом (заливкой) или штриховкой.

Для создания области служит команда Region, которая, помимо ввода с клавиатуры, может быть вызвана с помощью кнопки Region (Область), расположенной в инструментальной группе Draw (Рисование) вкладки Ноте (Главная).

При отработке команды Region необходимо вначале указать объекты, участвующие в создании контура области, а затем подтвердить окончание выборки нажатием Enter или щелчком правой кнопки мыши.

Объекты, участвующие в создании области, должны быть соединены в граничных точках с использованием режимов объектной привязки. В противном случае объединяемые сегменты могут не иметь общих точек, что приведет к игнорированию команды создания области. Также исключаются различные пересечения объектов между собой.
Команда Boundary является альтернативой команде Region. Вызов данной команды приводит к выводу на экран специального диалогового окна Boundary Creation (Границы образования). Данное окно подробно рассматривается в главе 6 «Сложные объекты».

Отличие Boundary от Region заключается в том, что в данном случае область создается исключительно из контура, образованного пересечением набора других объектов (областей, линий, дуг, прямоугольников и т.д.). При этом новый контур образуется через вершины пересечения исходных объектов (рис. 1.29). Вам достаточно воспользоваться диалоговым окном Boundary Creation (Границы образования) и указать точки, находящиеся внутри выделяемой области.

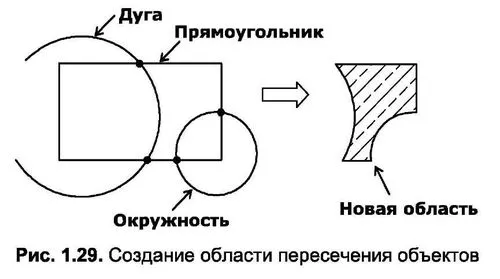
Одним из достоинств области считается возможность ее заполнения заливкой или штриховкой. Особый интерес при этом вызывает штриховка. Так, например, на рис. 1.29 выделенная область заполнена узором, состоящим из набора параллельных линий различного типа.

Для заполнения области подобными и другими узорами используйте команду Bhatch или кнопку Hatch (Штриховка), расположенную в инструментальной группе Draw (Рисование) вкладки Ноте (Главная).Открывшееся после этого окно позволяет выбрать различные типы штриховки, пользуясь специальными образцами, отсортированными по известным нормам и стандартам (рис. 1.30).

Примечание. Штриховка может применяться не только как узор, заполняющий область, – это самостоятельный и достаточно мощный объект AutoCAD, применяемый для решения различных задач.

БЛОКИ И ВНЕШНИЕ ССЫЛКИ

Блоком в AutoCAD называется группа объектов, обрабатываемая как одно целое. Примером блока может служить разработанный ранее чертеж, вставленный в текущий документ. При этом все объекты вставленного чертежа образуют один блок с определенным именем, с которым он хранится в базе данных чертежа.

С блоком можно связывать особый тип текстовых параметров (видимых или невидимых на чертеже), называемый атрибутом блока. Основное преимущество атрибута заключается в том, что его можно извлекать из чертежа и сохранять в виде текстового файла для дальнейшего применения.

Внешние ссылки — это особый тип блока, используемый для построения составных чертежей из элементов других чертежей. Основным отличием внешней ссылки от блока является то, что связанные с данной ссылкой чертежи не вставляются в чертеж, а хранятся в нем только как адресная ссылка. При каждом открытии чертежа, имеющего такие ссылки, AutoCAD находит их и выводит информацию о текущем состоянии этих ссылок.

Источник: autocad-lessons.com

Что называется невозможной фигурой в программе autocad

II Международный конкурс научно-исследовательских и творческих работ учащихся
Старт в науке

• Главная
• Список секций
• Математика
• НЕВОЗМОЖНЫЕ ФИГУРЫ

НЕВОЗМОЖНЫЕ ФИГУРЫ

Лановой Р.А. 1
Терентьева О.В. 1

Автор работы награжден дипломом победителя III степени

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

С некоторых пор меня заинтересовали такие фигуры, которые на первый взгляд кажутся обычными, а присмотревшись можно увидеть, что что-то в них не так. Основной интерес для меня представляли так называемые невозможные фигуры, посмотрев на которые создается впечатление, что существовать в реальном мире они не могут. Я захотел узнать о них больше.

«Мир невозможных фигур» одна из интереснейших тем, которая получила свое бурное развитее всего лишь в начале ХХ века. Однако, гораздо раньше, многие ученые и философы занимались этим вопросом. Даже такие простые объемные формы, как куб, пирамида, параллелепипед можно представить как комбинацию нескольких фигур, находящихся на разном расстоянии от глаза наблюдателя. Всегда при этом должна быть линия, по которой изображение отдельных частей совмещающих в целостную картину.

«Невозможная фигура — это выполненный на бумаге трехмерный объект, который не может существовать в действительности, но который, однако, можно видеть как двухмерное изображение». Это один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозможности существования такой фигуры в трёхмерном пространстве.

Передо мной встал вопрос: «Существуют ли в реальном мире невозможные фигуры?»

Цели проекта:

1.Выяснить, как создаются нереальные фигуры.

2. Найти области применения невозможных фигур.

1.Изучить литературы по теме «Невозможные фигуры».

2.Составить классификацию невозможных фигур.

3.Рассмотреть способы построения невозможных фигур.

4.Создать невозможную фигуру.

Тема моей работы актуальна ведь понимание парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Многие работы с нереальными объектами можно отнести к «интеллектуальным математическим играм».

Моделировать подобный мир можно только с помощью математических формул, человек представить его просто не в состоянии. И для развития пространственного воображения оказываются полезными невозможные фигуры. Человек неустанно мысленно создает вокруг себя то, что для него будет просто и понятно. Он даже не может себе представить, что некоторые объекты, окружающие его, могут быть «невозможными». На самом деле мир един, но рассматривать его можно с разных сторон.

Немного истории

Невозможные фигуры достаточно часто встречаются на древних гравюрах, картинах и иконах — в одних случаях мы имеем с явными ошибками передачи перспективы, в других — с умышленными искажениями, обусловленными художественным замыслом.

В средневековой японской и персидской живописи невозможные объекты являются неотъемлемой частью восточного художественного стиля, дающего лишь общий набросок картины, детали которой «приходится» додумывать зрителю самостоятельно, в соответствии со своими предпочтениями. Вот перед нами школа. Наше внимание привлекает архитектурное сооружение на заднем плане, геометрическая противоречивость которого очевидна. Его можно интерпретировать и как внутреннюю стену комнаты, и как наружную стену здания, но обе эти интерпретации неправильны, поскольку мы имеем дело с плоскостью, одновременно являющуюся и внешней, и наружной стенкой, то есть на картине изображен типичный невозможный объект.

Картины с искаженной перспективой встречаются уже в начале первого тысячелетия. На миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована Мадонна с младенцем. На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект нереальности.

Виды невозможных фигур.

«Невозможные фигуры» делятся на 4 группы. Итак, первая:

Удивительный треугольник – трибар.

Эта – фигура – возможно первый опубликованный в печати невозможный объект. Она появилась в 1958 году. Её авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как «трехмерную прямоугольную структуру». Она также получила название «трибар». С первого взгляда трибар кажется просто изображением равностороннего треугольника.

Но стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Если смотреть на каждую деталь отдельно, то она кажется реальной, но, в общем, эта фигура существовать не может. Она не деформирована, но при черчении были неправильно соединены правильные элементы.

Вот еще несколько примеров невозможных фигур на основе трибара.

Тройной деформированный трибар

Треугольник из 12 кубов

Бесконечная лестница

Эту фигуру чаще всего называют «Бесконечной лестницей», «Вечной лестницей» или «Лестницей Пенроуза» – по имени ее создателя. Ее также называют «непрерывно восходящей и нисходящей тропой».

Впервые эта фигура была опубликована в 1958 году. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом, человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути.

«Бесконечной лестницей» с успехом воспользовался художник Мауриц К. Эшер, на этот раз в своей литографии «Восхождение и нисхождение», созданной в 1960 году.

Лестница с четырьмя или семью ступеньками. На создание этой фигуры с большим количеством ступенек автора могла вдохновить куча обыкновенных железнодорожных шпал. Собравшись взобраться на эту лестницу, вы будете стоять перед выбором: подняться ли по четырем или по семи ступенькам.

Создатели этой лестницы воспользовались параллельными линиями при разработке конечных деталей блоков, находящихся на одинаковом расстоянии; кажется, что некоторые блоки перекручиваются, чтобы соответствовать иллюзии.

Космическая вилка.

Следующая группа фигур под общим названием «Космическая вилка». С этой фигурой мы входим в самую сердцевину и суть невозможного. Может быть, это самый многочисленный класс невозможных объектов.

Этот пресловутый невозможный объект с тремя (или с двумя?) зубцами стал популярен у инженеров и любителей головоломок в 1964 году. Первая публикация, посвященная необычной фигуре, появилась в декабре 1964 года. Автор назвал ее «Скобой, состоящей из трех элементов».

С практической точки зрения этот странный трезубец или механизм в виде скобы, абсолютно неприменим. Некоторые называют его просто «досадной ошибкой». Один из представителей аэрокосмической промышленности предложил использовать его свойства при конструировании межпространственного космического камертона.

Башня с четырьмя колоннами-близнецами.

Невозможные ящики

Еще один невозможный объект появился в 1966 году в Чикаго в результате оригинальных экспериментов фотографа доктора Чарльза Ф. Кокрана. Многие любители невозможных фигур проводили эксперименты с «Сумасшедшим ящиком». Первоначально автор назвал ее «Свободным ящиком» и заявил, что она была «сконструирована для пересылки невозможных объектов в большом количестве».

«Сумасшедший ящик» – это вывернутый наизнанку каркас куба. Непосредственным предшественником «Сумасшедшего ящика» была «Невозможная коробка» (автор Эшер), а ее предшественником в свою очередь стал куб Неккера.

Он не является невозможным объектом, однако представляет собой фигуру, в которой параметр глубины может восприниматься неоднозначно.

Когда мы вглядываемся в куб Неккера, то замечаем, что грань с точкой находится то на переднем, то на заднем плане, она перепрыгивает из одного положения в другое.

Оскар Рутерсвард – отец невозможной фигуры.

«Отцом» невозможных фигур считается шведский художник Оскар Рутерсвард. Шведский художник Оскар Рутерсвард, специалист по созданию изображений невозможных фигур утверждал, что плохо разбирается в математике, но, тем не менее, возвел свое искусство в ранг науки, создав целую теорию создания невозможных фигур по определенному ряду шаблонов.

Он разделил фигуры на две основные группы. Один из них он назвал «истинные невозможные фигуры». Это двухмерные изображения трёхмерных тел, которые на бумаге можно раскрасить и нанести на них тени, но у них нет монолитной и стабильной глубины.

Другой вид – сомнительные невозможные фигуры. Эти фигуры не представляют собой единых цельных тел. Они являются соединением двух или большего числа фигур. Их нельзя ни раскрасить, ни нанести на них свет и тени.

Истинная невозможная фигура состоит из фиксированного количества возможных элементов, а сомнительная «теряет» некоторое количество элементов, если за ними проследить глазами.

Один вариант этих невозможных фигур очень легко выполнить, и многие из тех, кто машинально чертит геометрические

фигуры, когда разговаривает по телефону, это уже не раз делали. Нужно провести пять, шесть или семь параллельных линий, закончить эти линии в разных концах по-разному – и невозможная фигура готова. Если, например, провести пять параллельных линий, то их можно закончить как две балки с одной стороны и три с другой.

На рисунке мы видим три варианта сомнительных невозможных фигур. Слева трех-семибалочник, построенный из семи линий, в котором три балки превращаются в семь. Фигура в середине, построенная из трех линий, в которой одна балка превращается в два круглых бруса. Фигура справа, построенная из четырех линий, в которой два круглых бруса превращаются в две балки

За свою жизнь Рутерсвард изобразил около 2500 фигур. Книги Рутерсварда опубликованы на многих языках, в том числе на русском.

Невозможные фигуры — возможны!

Многие полагают, что невозможные фигуры действительно невозможны, и их нельзя создать в реальном мире. Но надо помнить, что любой рисунок на листе бумаги — это проекция трехмерной фигуры. Следовательно, любая фигура, нарисованная на листе бумаги, должна существовать в трехмерном пространстве.

Невозможные объекты на картинах представляют собой проекции трехмерных объектов, а значит, объекты можно реализовать в виде скульптурных композиций. Существует множество способов их создания. Один из них — использование кривых линий в качестве сторон невозможного треугольника. Созданная скульптура выглядит невозможной только из единственной точки. Из этой точки кривые стороны выглядят прямыми, и поставленная цель будет достигнута — создан реальный «невозможный » объект.

Русский художник Анатолий Коненко, наш современник, разделил невозможные фигуры на 2 класса: одни можно смоделировать в реальности, а другие – нельзя. Модели невозможных фигур называются моделями Амес.

Я изготовил модель Амес своего невозможного ящика. Я взял сорок два кубика и склеил их, получился куб, в котором часть ребра отсутствует. Отмечу, что для создания полной иллюзии необходим правильный угол зрения и верное освещение.

Я изучил невозможные фигуры с применением теоремы Эйлера и пришёл к следующему выводу: теорема Эйлера, верная для любого выпуклого многогранника, неверна для невозможных фигур, но верна для их моделей Амес.

Я создаю свои невозможные фигуры, пользуясь советом О.Рутерсварда. Я начертил на бумаге семь параллельных отрезков. Соединил их снизу ломаной линией, а сверху придал им форму параллелепипедов. Посмотрите на нее сначала сверху потом снизу. Таких фигур можно придумать бесконечно много.

См. приложение.

Применение невозможных фигур

Невозможные фигуры находят иногда неожиданное применение. Оскар Рутерсвард рассказывает в книге «Omojliga figurer» об использовании рисунков имп-арта для психотерапии. Он пишет, что картины своими парадоксами вызывают удивление, заостряют внимание и желание расшифровать. Психолог Роджер Шепард использовал идею трезубца для своей картины невозможного слона.

В Швеции их применяют в зубоврачебной практике: рассматривая картины в приемной, пациенты отвлекаются от неприятных мыслей перед кабинетом стоматолога.

Невозможные фигуры вдохновили художников на создание целого нового направления в живописи, названного импоссибилизмом. К импоссибилистам относят голландского художника Эшера . Его перу принадлежат известные литографии «Водопад», «Восхождение и нисхождение» и «Бельведер». Художник использовал эффект «бесконечной лестницы», открытый Рутесвардом.

За рубежом, на улицах городов, мы можем увидеть архитектурные воплощения невозможных фигур.

Наиболее известное использование невозможных фигур в массовой культуре — логотип автоконцерна «Рено»

Математики утверждают, что и дворцы, в которых можно спуститься вниз по лестнице, ведущей вверх, могут существовать. Для этого нужно лишь построить такое сооружение не в трехмерном, а, скажем, в четырехмерном пространстве. А уж в виртуальном мире, который открывает нам современная компьютерная техника, и не такое можно натворить. Вот так в наши дни осуществляются задумки человека, который еще на заре века поверил в существование невозможных миров.

Заключение.

Невозможные фигуры заставляют наш разум сначала увидеть то, чего быть не должно, затем искать ответ — что же сделано не так, в чем скрыта изюминка парадокса. А ответ найти порой не так — то просто — он скрыт в оптическом, психологическом, логическом восприятии рисунков.

Развитие науки, необходимость мыслить по-новому, поиски прекрасного — все эти требования современной жизни заставляют искать новые методы, которые способны изменить пространственное мышление, воображение.

Изучив литературу по теме, я смог ответить на вопрос «Существуют ли в реальном мире невозможные фигуры?» Я понял, что невозможное возможно и нереальные фигуры можно сделать своими руками. Я создал модель Амес «Невозможного куба» и проверил на нем теорему Эйлера. Рассмотрев способы построения невозможных фигур, я смог нарисовать свои невозможные фигуры. Мне удалось показать, что

Вывод1: Все невозможные фигуры могут существовать в реальном мире.

Вывод2: Теорема Эйлера, верная для любого выпуклого многогранника, неверна для невозможных фигур, но верна для их моделей Амес.

Вывод3: Найдется ещё много областей, в которых будут использоваться невозможные фигуры.

Таким образом, можно сказать, что мир невозможных фигур чрезвычайно интересен и многообразен. Изучение невозможных фигур имеет довольно важное значение с точки зрения геометрии. Работа может быть использована на занятиях по математике для развития пространственного мышления учащихся. Для творческих людей, склонных к изобретательству, невозможные фигуры являются своеобразным рычагом для создания чего-то нового, необычного.

Список литературы

1. Левитин Карл Геометрическая рапсодия. — М.: Знание, 1984, -176 с.
2. Пенроуз Л., Пенроуз Р. Невозможные объекты, Квант, № 5,1971, с.26
3. Реутерсвард О. Невозможные фигуры. – М.: Стройиздат,1990, 206 с.
4. Ткачева М.В. Вращающиеся кубики. – М.: Дрофа, 2002. – 168 с.
5. Интернет ресурсы.

Источник: school-science.ru