Табулирование функции – это вычисление ее значений по изменяющимся значениям аргумента функции.
Табулируют функцию, например, для построения ее графика, для поиска ее максимальных значений. Табулирование функции y = f(x) ведется на некотором интервале значений аргумента x € [хн; хк], с изменением значений аргумента на одинаковую величину ∆х, которую называют шагом изменения х.
Пример. Разработать алгоритм табулирования функции y, приведенной на стр. 44, на интервале значений х € [хн; хк], с шагом ∆х изменения аргумента. Блок-схема алгоритма решения этой задачи приведена на рис. 10.
Рис. 11. Блок-схема алгоритма табулирования функции
“Блок 1” обеспечивает печать заголовка таблицы, а блок 9 – строк таблицы, чтобы получить таблицу следующего вида:
| x | y |
| хн | yн |
| х + ∆х | yн+1 |
| x + 2∆х | yн+2 |
| … | … |
| хк — ∆х | yк-1 |
| xк | yк |
“Блок 2”, “Блок 3” и “Блок 10” обеспечивают цикличность вычисления y в соответствии с изменением значения аргумента х от начального значения хн до конечного значения хк с шагом ∆х.
Табулирование функции, с++
Алгоритм поиска экстремальных значений (max, min )
Перед началом подсчета необходимо предусмотреть переменные (например, max и min), куда будут помещаться значения функции, подходящие в качестве соответственно максимального и минимального значения. Начальными значениями этим переменным могут быть присвоены такие, которые с высокой вероятностью не соответствуют истинным, например:
max = -1Е+38 min =1Е+38
Суть алгоритма поиска экстремальных значений в том, что в процессе табулирования, после вычисления очередного значения функции его сравнивают со значением max и min. Если это значение больше max, то оно принимается в качестве max, а если рассматриваемое значение меньше min, то его принимают в качестве min. В итоге, после вычисления последнего значения функции в переменных max и min окажутся соответственно самое большое и самое маленькое из всех вычисленных значений функции.
На рис. 12 приведен пример алгоритма нахождения максимальных и минимальных значений функции при ее табулировании в соответствии с алгоритмом, представленным на рис. 11.
В заключение отметим некоторые правила построения блок-схем алгоритмов:
— должно рационально использоваться имеющееся на листе место;
— размещение блоков схемы должно, по возможности, отражать последовательность выполнения операций, полагая их следование сверху вниз;
— исходящая линия “Да” должна быть направлена вниз;
— исходящая линия “Нет”, как правило, должна идти вправо;
— входящие в блоки линии входа должны быть направлены сверху;
— исходящие линии тока должны быть направлены вниз.
Рис. 12. Нахождение минимума и максимума
Источник: studopedia.su
Алгоритм в виде блок схемы
Составить блок-схему табулирования 2-ух функций — Pascal ABC
Табулирования 2-ух функций x и y. Здесь n — число слагаемых суммы s. Результат табулирования вывести в форме след таблицы: writeln(‘! ‘,x:2:1,’ ! ‘,y:9:8,’ ! ‘,s:9:8,’ ! ‘); сумма s=x-((x^3)/3!)+((x^5)/5!)-. Диапазон изменения x=[0,1;1] n=10 Функция y=sinx
Код к задаче: «Составить блок-схему табулирования 2-ух функций»
Листинг программы
const xn=0.1; xk=1.0; n=10; var x,dx,t,s,y:real; i,j:integer; begin dx:=(xk-xn)/(n-1); writeln(‘ ‘); writeln(‘—————————‘); writeln(‘| x | y | s |’); writeln(‘—————————‘); for i:=1 to n do begin x:=xn+(i-1)*dx; y:=sin(x); t:=x; s:=t; for j:=2 to n do begin t:=-t*x*x/(2*j-2)/(2*j-1); s:=s+t; end; writeln(‘|’,x:2:1,’|’,y:9:8,’|’,s:9:8,’|’); end; writeln(‘—————————‘); end.
Источник: studassistent.ru
Линейный алгоритм
Линейным называют алгоритм, операции и линии потоков которого идут по одному направлению, без повторений операций, без альтернативных путей потоков.
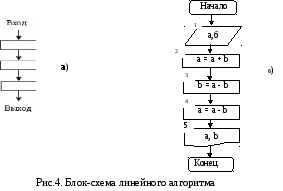
Блок-схема такого алгоритма имеет вид, представленный на рис. 4 а. Пример линейного алгоритма: имеются две переменные a и b, произвести обмен их значениями. Блок-схема алгоритма решения этой задачи приведена на рис. 4 б.
Следует отметить, что знак «=» в блоках 2, 3 и 4 означает не равенство, а операцию присвоения переменной значения. Например, в блоке 2 производится присвоение переменной а суммы значений переменных а и b.
В блок-схеме алгоритма все операции нумеруются (номер проставляется вверху слева от блока) в порядке их выполнения. Блоки «Начало» и «Конец» не нумеруются.
Ветвящийся алгоритм
Алгоритм называется ветвящимся (см. рис. 5), если в нем содержится блок перехода или условия, который имеет одну входную линию потока и более одной выходные линии.
Пример ветвящегося алгоритма: найти наибольшее значение трех переменных a, b и c. Блок-схема решения этого алгоритма приведена на рис. 6.
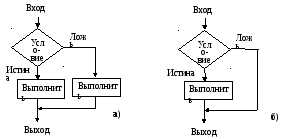
Рис. 5. Блок-схема ветвящегося алгоритма; а – полное ветвление, б – непол-ное ветвление.
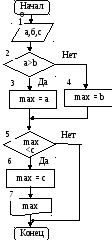
Рис. 6 . Блок схема алгоритма поиска максимального из трех значений
На рис. 7 приведен пример алгоритма вычисления значения переменной у, определяемой математическим выражением:
f
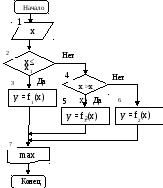1(x) если x ≤ x1
Рис. 7. Пример ветвящегося алгоритма
Циклический алгоритм
Алгоритм называется циклическим, если он содержит в своем составе последовательность действий (операторов, переходов), неоднократно повторяющуюся с заданием новых начальных условий. При этом алгоритм включает в себя процедуры задания этих начальных условий.
Часть алгоритма, отражающая эти действия, называется циклом
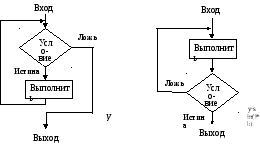
Как правило, алгоритмы решения реальных задач представляют собой комбинацию всех трех рассмотренных типов простейших алгоритмов. Рассмотрим алгоритмы некоторых часто встречающиеся задач.Рис. 8. Циклический алгоритм; а – цикл «пока», б – цикл «до».
Алгоритмы накопления суммы и произведения
В алгоритмах часто приходится накапливать сумму и произведение значений функции. Математическая запись суммы имеет вид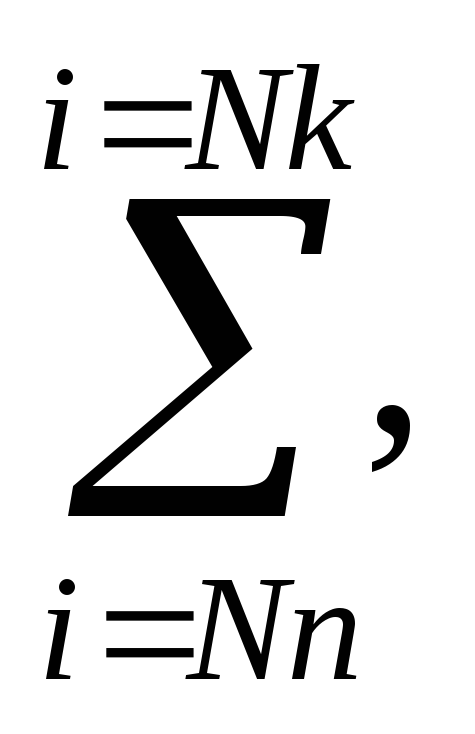 
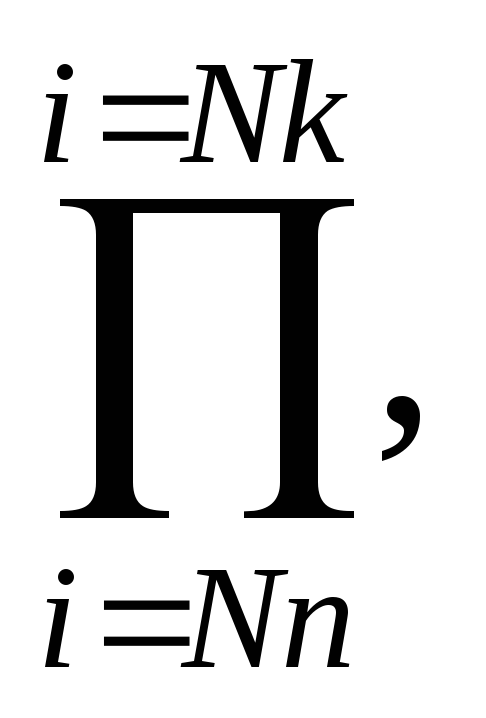гдеNn – начальные значений переменной, Nk – конечное значение целочисленной переменной i.
Перед началом процесса накопления суммы переменной, в которой будет использоваться сумма, необходимо присвоить значение 0. Иначе при объявлении переменной и выделения места в памяти ЭВМ, в этом месте может оказаться любая информация от предыдущих операций, и мы можем получить неверную сумму.
При подсчете произведения переменной, в которой будет накапливаться произведение, необходимо присвоить начальное значение 1.
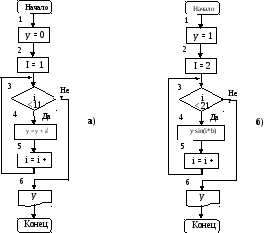
Рис. 9. Блок схемы алгоритмов накопления
а) – суммы y =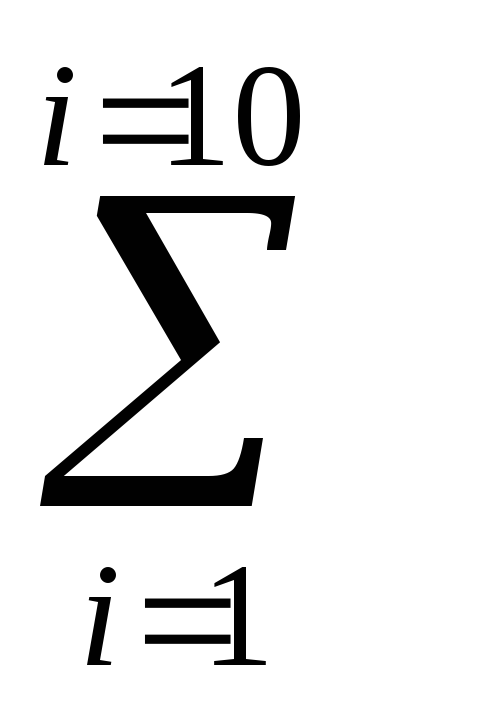 
a i и б) — произведения y = 
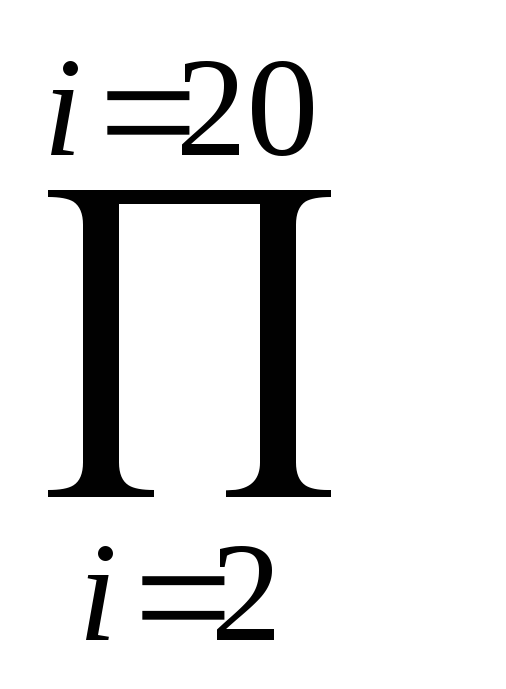sin(I*b)
Алгоритм табулирования функции
Табулирование функции – это вычисление ее значений по изменяющимся значениям аргумента функции.
Табулируют функцию, например, для построения ее графика, для поиска ее максимальных значений. Табулирование функции y = f(x) ведется на некотором интервале значений аргумента x € [хн; хк], с изменением значений аргумента на одинаковую величину ∆х, которую называют шагом изменения х.
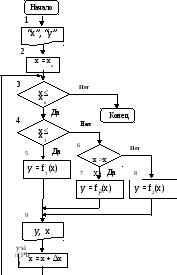
Пример. Разработать алгоритм табулирования функции y, приведенной на стр. 44, на интервале значений х € [хн; хк], с шагом ∆х изменения аргумента. Блок-схема алгоритма решения этой задачи приведена на рис. 10.
Рис. 11. Блок-схема алгоритма табулирования функции
“Блок 1” обеспечивает печать заголовка таблицы, а блок 9 – строк таблицы, чтобы получить таблицу следующего вида:
Источник: studfile.net