Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
Обозначим исходные данные как М u N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(М, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если M>N, то
#7 Как автоматически построить блок схему из JavaScript кода
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М u N (M> N). Это значит, что М = mК, N = nК, где m, n — натуральные числа, причем m > n. Тогда М — N = К(m — n), откуда следует, что К — делитель числа М — N. Значит, все общие делители чисел М и N являются делителями их разности М — N, в том числе и наибольший общий делитель.
Второе очевидное свойство:
Для «ручного» счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) заменить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
Получили: НОД(32, 24) =НОД(8, 8) = 8, что верно.
Описание алгоритма Евклида блок-схемой
На рис. 3.12 приведена блок-схема алгоритма Евклида.
| Рис. 3.12. Блок-схема алгоритма Евклида |
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24.
| Шаг | Операция | M | N | Условие |
| 1 | ввод М | 32 | ||
| 2 | ввод N | 24 | ||
| 3 | M ¹ N | 32 ¹ 24, да | ||
| 4 | M>N | 32>24, да | ||
| 5 | M:=M-N | 8 | ||
| 6 | M ¹ N | 8 ¹ 24, да | ||
| 7 | M>N | 8>24, нет | ||
| 8 | N:=N-M | 16 | ||
| 9 | M ¹ N | 8 ¹ 16, да | ||
| 10 | M>N | 8>16, нет | ||
| 11 | N:=N-M | 8 | ||
| 12 | M ¹ N | 8 ¹ 8, нет | ||
| 13 | вывод M | 8 | ||
| 14 | конец |
Блок-схема циклического алгоритма. Вычисление n!
В итоге получился верный результат.
Программа на АЯ и на Паскале
Запишем алгоритм на АЯ и программу на Паскале.
| алг Евклид цел М, N нач вывод » Введите М и N» ввод М, N пока М N, повторять нц если M>N то M:=M-N иначе N:=N-M кв кц вывод «НОД=»,М кон |
Program Evklid; var M, N: integer; begin writeln(‘Введите М и N’); readln(M, N); while M<>N do begin if M>N then M:=M-N else N:=N-M end; write(‘Н0Д=’,М) end. |
1. Выполните на компьютере программу Evklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
Алгоритм Евклида — нахождение наибольшего общего делителя
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.
Алгоритм нахождения НОД делением
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6
В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для НОД находим сумму этих переменных.
Поскольку в одной из переменных ноль, он не оказывает влияние на результат.
Алгоритм нахождения НОД вычитанием
- Из большего числа вычитаем меньшее.
- Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
- Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6
Функция вычисления НОД
Блок-схема алгоритма Евклида
Примечание. В модуле math языка программирования Python есть функция gcd(), вычисляющая наибольший общий делитель двух чисел.
Наибольший общий делитель и наименьшее общее кратное.
В этом уроке мы поговорим о том как вычислять НОД и НОК. Дело в том, что элементарные арифметические вычисления должен уметь делать любой программист, так как алгоритм вычисления можно встретить во многих программах. Тем более вы их уже должны знать, если вы учились в школе 5 классе.
Наибольший общий делитель. НОД.
Для нахождения общего делителя вам нужно знать следующее:
Запомните: наибольший общий делитель (НОД) двух целых чисел – это наибольшее целое число, на которое делятся оба исходных числа без остатка. Однако одно из исходных чисел должно быть большее нуля.
Запомните: если у вас одно из двух чисел ноль, то НОД будет, то число что больше ноля.
Запомните: существует понятие взаимно-простых чисел, у которого нет общих делителей, кроме единицы. К примеру число 5 и 4, НОД этих чисел будет равен 1, так как если 5 разделить на 4 вы не получите целое число без остатка, следовательно НОД=1
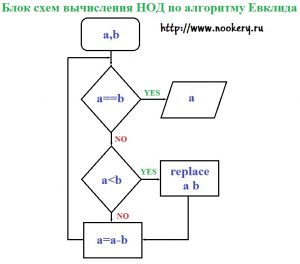
Все остальные числа, у которых НОД больше 1, вычисляются по принципу бинарного алгоритма или с помощью алгоритма Евклида. В этой статье мы подробно разберем алгоритм Евклида, который еще называют взаимным вычитанием, поскольку НОД получается при последовательном вычитании меньшего из большего. Используем алгоритм Евклида в нашем примере НОД(12, 30). По алгоритму Евклида нам надо вычесть из большее меньшее, то есть из 30-12-12=6 В числе 30 у нас может поместиться число 12 только два раза, число 12 называют кратным, и остатком останется число 6. Теперь нам надо из числа 30 отнять кратное числа 6, которое у нас получилось, 30-6-6-6-6-6=5 НОД числа 12 и 30 будет равен 6. Так как нам надо найти именно наибольший делитель в нашем случаи 6 больше 5, следовательно НОД(12,30)=6. Как видите ничего сложного, теперь давайте составим блок схему.
Блок-схема «Алгоритм Евклида»
Наименьшее общее кратное(НОК).
В целом ничего сложного, главное не запутаться, сейчас мы нарисуем блок схему наименьшего общего кратного (НОК).
Блок схема Наименьшего общего кратного (НОК)
рис 3.
Алгоритм работы программы описан вначале, статьи о НОК.
Но как же быть если нам надо к примеру найти НОД трех и более натуральных чисел, или найти НОК трех или более натуральных чисел. Тут ничего сложного инструкцию по нахождению НОД из 3 чисел и НОК смотрим ниже.
-
Сравниваем все числа К примеру a Блок схема НОД алгоритма трех чисел, четырех чисел итд.
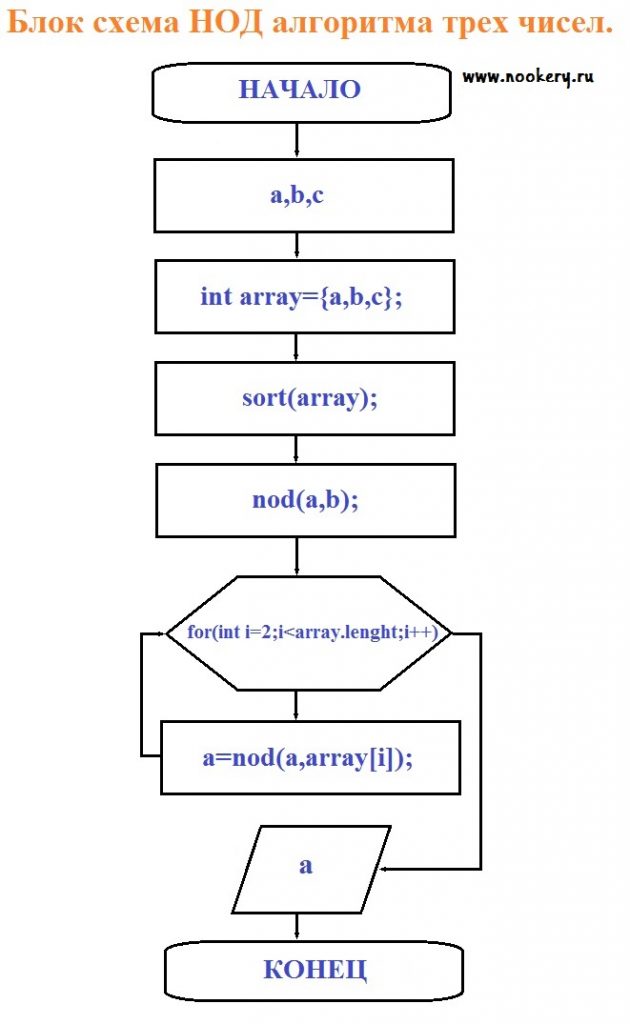
Разберем по подробнее работу программы блок схемы из рис. 4.
- У нас подается 3 числа, но их может быть сколько угодно.
- Их мы записываем в массив array.
- Выполняем метод sort(); Это мой метод он принимает массив чисел, делает сортировку по убыванию, пузырьковым методом, о нем вы можете прочитать из уроков о массивах.
- Выполняем метод nod(), который принимает первые два числа. Я создал метод по аналогии как написано выше в этой статье.
- В следующем блоке я помещаю в тело цикла метод nod(), который присваиваю возвращаемое число из метода nod() переменной a.
- Выводим результат.
- Завершаем работу программы.
Скачать калькулятор НОК и НОД .
Пока писал статью, написал программу НОК и НОД вычисления, которую можете скачать с сайта. Работа программы очень простая, достаточно в текстовое поле вписать цифры через пробел или запятую, нажать на кнопку вычислить или Enter и программа выведет результат. Программа написана на языке java. Может запускаться со всех систем.
Скачать калькулятор НОК и НОД .
Уроки 46 — 47
Сочетание циклов и ветвлений. Алгоритм Евклида
(§ 16. Алгоритм Евклида)
Использование алгоритма Евклида при решении задач
Алгоритм Евклида
Алгоритм Евклида






Наибольший общий делитель
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они оба делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НОД(12, 18) = 6.
Обозначим исходные данные как М и N. Постановка задачи выглядит следующим образом:
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если M > N, то
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М и N (М > N). Это значит, что М = mК, N = nК, где m, n — натуральные числа, причем m > n. Тогда М — N = К(m — n), откуда следует, что К — делитель числа М — N. Значит, все общие делители чисел М и N являются делителями их разности М — N, в том числе и наибольший общий делитель.
Второе очевидное свойство:
Для «ручного» счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) заменить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
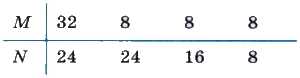
Получили: НОД(32, 24) = НОД(8, 8) = 8, что верно.
Описание алгоритма Евклида блок-схемой
На рисунке 2.8 приведена блок-схема алгоритма Евклида.
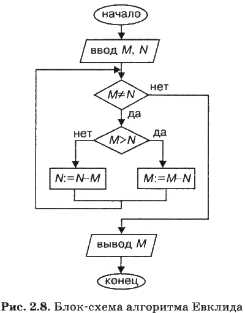
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24:
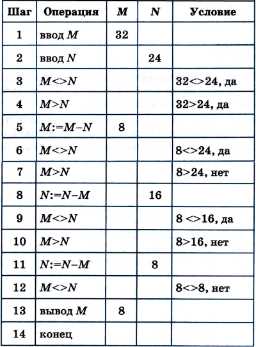
В итоге получился верный результат.

Коротко о главном
Алгоритм Евклида предназначен для получения наибольшего общего делителя двух натуральных чисел. Структура алгоритма Евклида — цикл с вложенным ветвлением.
Ручная трассировка может использоваться для проверки правильности лишь сравнительно простых алгоритмов. Поиск алгоритмических ошибок в программе производится с помощью тестирования.
Вопросы и задания
1. Выполните на компьютере программу Evklid (из параграфа). Протестируйте ее на значениях М = 32, N = 24; М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:


Следующая страница Дополнительный материал к главе II (§§ 8 — 21). Сложность алгоритмов
Источник: remnabor.net
Представления алгоритмов
Рассмотрим способы представления алгоритмов на примере алгоритма Евклида (алгоритма нахождения наибольшего общего делителя двух натуральных чисел).
Алгоритм Евклида для нахождения НОД двух натуральных чисел заключается в следующем: большее из чисел делится на меньшее, затем делитель делится на полученный остаток до тех пор пока остаток не станет равным нулю. Последний ненулевой остаток дает НОД чисел.
Обозначим наибольший общий делитель двух чисел и через , а остаток от деления на – через .
Легко находим НОК или НОД с помощью алгоритма Евклида
Любая сложная задача всегда может быть разбита на несколько простых задач. Те в свою очередь могут быть разбиты на ещё1 более мелкие задачи. В олимпиадных задачах по программированию очень часто требуется найти НОД(наибольший общий делитель) или НОК(наименьшее общее кратное) двух или более чисел. Это может быть задача по фасовке предметам по ящикам (целочисленное деление) или формирование людей в бригады. Короче там где нужно искать целые числа после деления.
Пример двух чисел 6 и 15. Очевидно, что НОД (наибольшим общим делителем) будет число 3. А далее находим НОК (наименьшее) общее кратное). Которое будет равно 30.
Для небольших чисел это легко вычисляется в уме. Но вот с пятиначными числами, так легко не получится. Поэтому предлагаю обратиться к алгоритму Евклида. Математические выкладки и детали в данной статье затрагивать не буду, хотя там много есть интересного.
Но суть достаточно простая. Их двух чисел выбираем большее и аычитаем из него меньшее. Далее выбираем снова большое и вычитаем из него снова, до тех пор пока разница не будет равна одному из чисел. Это и будет искомое число. Предлагаю проверить сперва на очевидных примерха.