Рабочая программа разработана на основе программы четырёхлетней начальной школы УМК «Школа России» система уроков по учебнику «Математика. 1 класс» (в 2 частях), 2016г. Авторы: М.И.Моро, С.В.Степанова.
Валеева Елена Сергеевна
Содержимое разработки
РАБОЧАЯ ПРОГРАММА ПО ПРЕДМЕТУ «МАТЕМАТИКА»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа курса «Математика» разработана на основе Федерального государственного образовательного стандарта начального общего образования, Концепции духовно-нравственного развития и воспитания личности гражданина России, планируемых результатов начального общего образования и авторской программы М.И. Моро, Ю.М. Колягина, М.А. Бантовой, Г.В. Бельтюковой, С.И.
Волковой, С.В. Степановой «Математика. 1-4 классы».
Начальное обучение математике закладывает основы для формирования приёмов умственной деятельности: школьники учатся проводить анализ, сравнение, классификацию объектов, устанавливать причинно-следственные связи, закономерности, выстраивать логические цепочки рассуждений. Изучая математику, они усваивают определённые обобщённые знания и способы действий. Универсальные математические способы познания способствуют целостному восприятию мира, позволяют выстраивать модели его отдельных процессов и явлений, а также являются основой формирования универсальных учебных действий. Универсальные учебные действия обеспечивают усвоение предметных знаний и интеллектуальное развитие учащихся, формируют способность к самостоятельному поиску и усвоению новой информации, новых знаний и способов действий, что составляет основу умения учиться.
Математика 4 класс (Урок№1 — Нумерация. Счёт предметов. Разряды.)
Усвоенные в начальном курсе математики знания и способы действий необходимы не только для дальнейшего успешного изучения математики и других школьных дисциплин, но и для решения многих практических задач во взрослой жизни.
Основными целями начального обучения математике являются:
— математическое развитие младших школьников;
— освоение начальных математических знаний;
— развитие интереса к математике, стремление использовать математические знания в повседневной жизни;
— привитие умений и качеств, необходимых человеку ХХI века.
Программа определяет ряд задач, решение которых направлено на достижение основных целей начального математического образования:
— формирование элементов самостоятельной интеллектуальной деятельности на основе овладения несложными математическими методами познания окружающего мира (умения устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения);
— развитие основ логического, знаково-символического и алгоритмического мышления;
— развитие пространственного воображения;
— развитие математической речи;
— формирование системы начальных математических знаний и умение их применять для решения учебно-познавательных и практических задач;
— формирование умения вести поиск информации и работать с ней;
Сравнительный анализ современного учебника по математике за 2 класс и учебника СССР.
— формирование первоначальных представлений о компьютерной грамотности;
— развитие познавательных способностей;
— воспитание стремления к расширению математических знаний;
— формирование критичности мышления;
— развитие умений аргументировано обосновывать и отстаивать высказанное суждение, оценивать и принимать суждения других.
Решение названных задач обеспечит осознание младшими школьниками универсальности математических способов познания мира, усвоение начальных математических знаний, связей математики с окружающей действительностью и с другими школьными предметами, а также личностную заинтересованность в расширении математических знаний.
Начальный курс математики является курсом интегрированным: в нём объединён арифметический, геометрический и алгебраический материал.
Математические знания и представления о числах, величинах, геометрических фигурах лежат в основе формирования общей картины мира и познания законов его развития. Именно эти знания и представления необходимы для целостного восприятия объектов и явлений природы, многочисленных памятников культуры, сокровищ искусства.
В соответствии с Образовательной программой школы, рабочая программа по математике рассчитана на 132 часа в год при 4 часах в неделю (33 учебные недели).
Для реализации программного содержания используются следующие учебные пособия:
1. Моро М.И. Математика: учебник для 1 класса: в 2 частях / М.И. Моро, С.И. Волкова, С.В. Степанова. — М.: Просвещение, 2016.
2. Моро М.И. Тетрадь по математике для 1 класса: в 2 частях/ М.И. Моро, С.И. Волкова. — М.: Просвещение, 2016.
3. Электронное приложение к учебнику «Математика», 1 класс (диск СD-RОМ), автор М.И. Моро.
УЧЕБНО — ТЕМАТИЧЕСКИЙ ПЛАН
Наименование разделов
Всего часов
Подготовка к изучению чисел. Пространственные и временные представления
Числа от 1 до 10. Число 0. Нумерация
Числа от 1 до 10. Сложение и вычитание
Числа от 1 до 20. Нумерация
Числа от 1 до 20. Сложение и вычитание
Примечание: в планировании предусмотрены резервные уроки, которые учитель может использовать как дополнительные. Они могут быть резервными при карантине или других форс-мажорных обстоятельствах.
СОДЕРЖАНИЕ ПРОГРАММЫ
Подготовка к изучению чисел. Пространственные и временные представления
Признаки предметов. Сравнение предметов по размеру (больше — меньше, выше — ниже, длиннее — короче) и по форме (круглый, квадратный, треугольный и т.д.).
Взаимное расположение предметов в пространстве и на плоскости (выше — ниже, слева — справа, за — перед, между, вверху — внизу, ближе — дальше и др.).
Направления движения: слева направо, справа налево, сверху вниз, снизу вверх.
Временные представления: сначала, потом, до, после, раньше, позже.
Сравнение групп предметов: больше, меньше, столько же, на сколько больше (меньше).
Числа от 1 до 10. Число 0. Нумерация (27 часов)
Название, последовательность и обозначение чисел от 1 до 10. Счет реальных предметов и их изображений, движений, звуков и др. Получение числа путем прибавления единицы к предыдущему, вычитания единицы из числа, следующего за данным при счете.
Число 0. Его получение и обозначение.
Равенство, неравенство. Знаки , =.
Состав чисел в пределах первого десятка.
Точка. Линии (кривая, прямая). Отрезок. Ломаная. Многоугольник.
Углы, вершины и стороны многоугольника.
Длина отрезка. Сантиметр.
Решение задач в одно действие на сложение и вычитание (на основе пересчета предметов).
Практическая работа: сравнение длин отрезков, измерение длины отрезка, построение отрезка заданной длины.
Числа от 1 до 10. Сложение и вычитание (54 часа)
Конкретный смысл и названия действий сложения и вычитания. Знаки «=», «—«, «+».
Названия компонентов и результатов сложения и вычитания (их использование при чтении и записи числовых выражений). Нахождение значений числовых выражений в одно два действия без скобок.
Переместительное свойство сложения.
Приемы вычислений: прибавление числа по частям, перестановка чисел; вычитание числа по частям и вычитание на основе знания соответствующего случая сложения.
Таблица сложения в пределах 10. Соответствующие случаи вычитания.
Сложение и вычитание с числом 0.
Нахождение числа, которое на несколько единиц больше или меньше данного.
Решение задач в одно действие на сложение и вычитание.
Числа от 1 до 20. Нумерация (12 часов)
Название и последовательность чисел от 1 до 20. десятичный состав чисел от 11 до 20. Чтение и запись чисел от 11 до 20. Сравнение чисел.
Сложение и вычитание чисел вида 10+8, 18—8 18—10.
Сравнение чисел с помощью вычитания.
Единица времени: час. Определение времени по часам с точностью до часа.
Единицы длины: сантиметр, дециметр. Соотношение между ними. Построение отрез ков заданной длины.
Единицы массы: килограмм.
Единицы объема: литр.
Числа от 1 до 20. Сложение и вычитание (22 часа)
Сложение двух однозначных чисел, сумма которых больше 10, с использованием изученных приемов вычислений.
Таблица сложения и соответствующие случаи вычитания.
Решение задач в одно-два действия на сложение и вычитание.
Итоговое повторение (6 часов)
Числа от 1 до 20. Нумерация.
Табличное сложение и вычитание.
Геометрические фигуры (квадрат, треугольник, прямоугольник, многоугольник). Измерение и построение отрезков.
Решение задач изученных видов.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ
К концу первого класса учащийся научится:
— назвать числа от 0 до 20; называть и обозначать действия сложения и вычитания;
— называть результаты сложения чисел в пределах 10 и соответствующие случаи вычитания;
— называть результаты сложения чисел в пределах 20 и соответствующие случаи вычитания;
— оценивать количество предметов числом и проверять результат подсчетом в пределах 20;
— вести счет как в прямом, так и в обратном порядке в пределах 20;
— записывать и сравнивать числа в пределах 20;
— находить значение числового выражения в 1-2 действия в пределах 20 (без скобок);
— решать задачи в 1-2 действия, раскрывающие конкретный смысл действий сложения и вычитания, а также задачи на нахождение числа, которое на несколько единиц больше (меньше) данного;
— проводить измерение длины отрезка и длины ломаной;
— строить отрезок заданной длины.
К концу обучения в первом классе ученик получит возможность научиться:
— сравнивать и упорядочивать объекты по разным признакам: длине, массе, вместимости;
— решать задачи, связанные с бытовыми жизненными ситуациями (покупка, измерение, взвешивание и др.);
— оценивать величины предметов на глаз.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ ПРЕДМЕТА
Программа обеспечивает достижение первоклассниками следующих личностных, метапредметных и предметных результатов.
Изучение курса «Математика» в первом классе направлено на получение следующих личностных результатов:
— чувство гордости за свою Родину, российский народ и историю России;
— осознание роли своей страны в мировом развитии, уважительное отношение к семейным ценностям, бережное отношение к окружающему миру;
— целостное восприятие окружающего мира;
— развитая мотивация учебной деятельности и личностного смысла учения, заинтересованность в приобретении и расширении знаний и способов действий, творческий подход к выполнению заданий;
— рефлексивная самооценка, умение анализировать свои действия и управлять ими;
— навыки сотрудничества со взрослыми и сверстниками;
— установка на здоровый образ жизни, наличие мотивации к творческому труду, к работе на результат.
Метапредметными результатами изучения курса «Математика» в первом классе является формирование регулятивных, познавательных и коммуникативных универсальных учебных действий.
Регулятивные универсальные учебные действия:
— способность понимать, принимать и сохранять учебную задачу, соответствующую этапу обучения, ориентироваться в учебном материале, предоставляющем средства для ее решения;
— сформированность на начальном этапе умений планировать учебные действия (два-три шага) в соответствии с поставленной задачей;
— начальный уровень сформированности умений проводить самоконтроль и самооценку результатов своей учебной деятельности.
Познавательные универсальные учебные действия:
— осознанное чтение, построение речевых высказываний, использование введенных математических символов, знаков, терминов математической речи;
— первоначальные методы нахождения и чтения информации, представленной разными способами (текст, таблица) в разных носителях (учебник, справочник, аудио- и видеоматериалы и др.);
— начальное освоение способов решения задач творческого и поискового характера;
— первоначальные умения использования знаково-символических средств представления информации для создания моделей изучаемых объектов, в том числе и при решении текстовых задач;
— способность излагать свое мнение и аргументировать его;
— начальный уровень овладения логическими действиями сравнения, анализа, синтеза, обобщения, классификации по разным признакам на доступном материале;
— овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации по родовидовым признакам, установления аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям;
— овладение базовыми предметными и межпредметными понятиями, отражающими существенные связи и отношения между объектами и процессами.
Коммуникативные универсальные учебные действия:
— готовность слушать собеседника и вести диалог; готовность признать возможность существования различных точек зрения и права каждого иметь свою; излагать своё мнение и аргументировать свою точку зрения;
— способность определять общую цель и пути её достижения;
— способность договариваться о распределении функций и ролей в совместной деятельности, осуществлять взаимный контроль в совместной деятельности, адекватно оценивать собственное поведение и поведение окружающих.
Предметными результатами изучения курса являются:
— использование приобретённых математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также для оценки их количественных и пространственных отношений;
— овладение основами логического и алгоритмического мышления, пространственного воображения и математической речи, основами счёта, измерения, прикидки результата и его оценки, наглядного представления данных в разной форме (таблицы, схемы, диаграммы), записи и выполнения алгоритмов;
— приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач;
— выполнение устно и письменно арифметических действий с числами и числовыми выражениями, решение текстовых задач, выполнение и построение алгоритмов и стратегий в игре: исследование, распознавание и изображение геометрических фигур, работа с таблицами, схемами, графиками и диаграммами, цепочками; представление, анализ и интерпретация данных;
— приобретение первоначальных навыков работы на компьютере (набирать текст на клавиатуре).
СИСТЕМА ОЦЕНКИ ДОСТИЖЕНИЯ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ
ОСВОЕНИЯ ПРЕДМЕТА. КРИТЕРИИ ОЦЕНИВАНИЯ
В соответствии с требованиями Федерального государственного образовательного стандарта начального общего образования, необходимо использовать систему оценки, ориентированную на выявление и оценку образовательных достижений учащихся с целью итоговой оценки подготовки выпускников на ступени начального общего образования. Особенностями такой системы оценки являются:
— комплексный подход к оценке результатов образования (оценка предметных, метапредметных и личностных результатов общего образования);
— использование планируемых результатов освоения основных образовательных программ в качестве содержательной и критериальной базы оценки;
— оценка динамики образовательных достижений обучающихся;
— сочетание внешней и внутренней оценки как механизма обеспечения качества образования;
— использование накопительной системы оценивания (портфолио), характеризующей динамику индивидуальных образовательных достижений;
— использование наряду со стандартизированными письменными или устными работами таких форм и методов оценки, как проекты, практические работы, творческие работы, самоанализ, самооценка, наблюдения и др.
В первом классе ведется безотметочное обучение, основная цель которого — сформировать и развить оценочную деятельность детей, сделать педагогический процесс гуманным и направленным на развитие личности ребенка. Необходимо учитывать, что это не обучение традиционного вида, из которого изъяты отметки, а качественно новое обучение в начальных классах — на содержательно-оценочной основе.
При использовании безотметочной системы нельзя оценивать личностныё качества:
особенности памяти, внимания, восприятия. Оцениванию подлежат интеллектуальные, творческие и инициативные проявления ребёнка: умные вопросы, самостоятельный поиск, изучение дополнительного учебного материала и др.
Системная оценка личностных, метапредметных и предметных результатов реализуется в рамках накопительной системы — рабочего Портфолио. Система оценки достижения планируемых результатов изучения математики предполагает комплексный уровневый подход к оценке результатов обучения. Объектом оценки предметных результатов служит способность первоклассников решать учебно-познавательные и учебно-практические задачи. Оценка индивидуальных образовательных достижений ведётся «методом сложения», при котором фиксируется достижение опорного уровня и его превышение.
Портфолио ученика:
— является современным педагогическим инструментом сопровождения развития и оценки достижений учащихся, ориентированным на обновление и совершенствование качества образования;
— реализует одно из основных положений Федеральных государственных образовательных стандартов общего образования второго поколения — формирование универсальных учебных действий;
— позволяет учитывать возрастные особенности развития универсальных учебных действий учащихся младших классов; лучшие достижения Российской школы на этапе начального обучения; а также педагогические ресурсы учебных предметов образовательного плана;
— предполагает активное вовлечение учащихся в оценочную деятельность на основе проблемного анализа, рефлексии и оптимистического прогнозирования.
Преимущества рабочего Портфолио как метода оценивания достижений учащихся заключаются в следующем:
— сфокусирован на процессуальном контроле новых приоритетов современного образования, которыми являются УУД (универсальные учебные действия);
— учитывает особенности развития критического мышления учащихся путем использования трех стадий: вызов (проблемная ситуация) — осмысление — рефлексия;
— позволяет помочь учащимся самим определять цели обучения, осуществлять активное присвоение информации и размышлять о том, что они узнали.
В рабочих тетрадях по математике для первого класса учащимся предлагаются странички для контроля и самоконтроля овладения предметными результатами обучения математики «Что узнали? Чему научились».
Источник: videouroki.net
Программа по математике по УМК «Школа России» авторов М.И. Моро, Ю.М.Колягина, М.А. Бантовой, Г.В. Бельтюковой, С.И.Волковой, С.В. Степановой «Математика. 1 – 4 классы»
рабочая программа по математике по теме
Рабочая программа предмета «Математика» составлена на основе Федерального государственного стандарта начального общего образования, Примерной программы начального общего образования по математике для образовательных учреждений и программы общеобразовательных учреждений авторов М.И. Моро, Ю.М.Колягина, М.А. Бантовой, Г.В. Бельтюковой, С.И.Волковой, С.В. Степановой «Математика.
1 – 4 классы» (учебно – методический комплект «Школа России»).
Скачать:
Предварительный просмотр:
Рабочая программа предмета «Математика» составлена на основе Федерального государственного стандарта начального общего образования, Примерной программы начального общего образования по математике для образовательных учреждений и программы общеобразовательных учреждений авторов М.И. Моро, Ю.М.Колягина, М.А. Бантовой, Г.В. Бельтюковой, С.И.Волковой, С.В. Степановой «Математика.
1 – 4 классы» (учебно – методический комплект «Школа России»).
Рабочая программа разработана в целях конкретизации содержания образовательного стандарта с учетом межпредметных и внутрипредметных связей, логики учебного процесса и возрастных особенностей младших школьников. Обучение математике является важнейшей составляющей начального общего образования. Этот предмет играет важную роль в формировании у младших школьников умения учиться.
Начальное обучение математике закладывает основы для формирования приемов умственной деятельности: школьники учатся проводить анализ, сравнение, классификацию объектов, устанавливать причинно – следственные связи, закономерности, выстраивать логические цепочки рассуждений. Изучая математику, учащиеся усваивают определенные обобщенные знания и способы действий. Универсальные математические познания способствуют целостному восприятию мира, позволяют выстраивать модели его отдельных процессов и явлений, а также являются основой формирования универсальных учебных действий. Универсальные учебные действия обеспечивают усвоение предметных знаний и интеллектуальное развитие учащихся, формируют способность к самостоятельному поиску и усвоению новой информации, новых знаний и способов действий, что составляет основу умения учиться.
Основными целями начального обучения математики являются:
- Математическое развитие младших школьников
- Формирование системы начальных математических знаний
- Воспитание интереса к математике, к умственной деятельности
Общая характеристика учебного предмета
Программа определяет ряд задач , решение которых направлено на достижение основных целей начального математического образования:
— формирование элементов самостоятельной интеллектуальной деятельности на основе овладения несложными математическими методами познания окружающего мира (умения устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения);
— развитие основ логического, знаково – символического и алгоритмического мышления;
— развитие пространственного воображения;
— развитие математической речи;
— формирование системы начальных математических знаний и умений, умение их применять для решения учебно – познавательных и практических задач;
— формирование вести поиск информации и работать с ней;
— формирование первоначальных представлений о компьютерной грамотности;
— развитие познавательных способностей;
— воспитание стремления к расширению математических знаний;
— формирование критичности мышления;
— развитие умений аргументировано обосновывать и отстаивать высказанное суждение, оценивать и принимать суждения других.
Решение названных задач обеспечит осознание младшими школьниками универсальности математических способов познания мира, усвоение начальных математических знаний, связей математики с окружающей действительностью и другими школьными предметами, а также личную заинтересованность в расширении математических знаний.
Начальный курс математики является курсом интегрированным: в нем объединен арифметический, геометрический и алгебраический материал.
Содержание обучения представлено в программе разделами: «Числа и величины», «Арифметические действия», «Текстовые задачи», «Пространственные отношения. Геометрические фигуры», «Геометрические величины», «Работа с информацией».
Основа арифметического содержания – представления о натуральном числе и нуле, арифметических действиях (сложение, вычитание, умножение и деление). На уроках математики у младших школьников будут сформированы представления о числе как результате счёта, о принципах образования, записи и сравнения целых неотрицательных чисел. Учащиеся научатся выполнять устно и письменно арифметические действия с целыми неотрицательными числами в пределах миллиона; узнают, как связаны между собой компоненты и результаты арифметических действий; научатся находить неизвестный компонент арифметического действия по известному компоненту и результату действия; усвоят связи между сложением и вычитанием, умножением и делением; освоят различные приёмы проверки выполненных вычислений. Младшие школьники познакомятся с калькулятором и научатся пользоваться им при выполнении некоторых вычислений, в частности при проверке результатов арифметических действий с многозначными числами.
Программа предусматривает ознакомление с величинами (длин а , площадь, масс а , вместимость, время) и их измерением, с единицами измерения однородных величин и соотношениями между ними.
Важной особенностью программы является включение в неё элементов алгебраической пропедевтики (выражения с буквой, уравнения и их решение). Как показывает многолетняя школьная практика, такой материал в начальном курсе математики позволяет повысить уровень формируемых обобщений, способствует более глубокому осознанию взаимосвязей между компонентами и результатом арифметических действий, расширяет основу для восприятия функциональной зависимости между величинами, обеспечивает готовность выпускников начальных классов к дальнейшему освоению алгебраического содержания школьного курса математики.
Особое место в содержании начального математического образования занимают текстовые задачи. Работа с ними в данном курсе имеет свою специфику и требует более детального рассмотрения.
Система подбора задач, определение времени и последовательности введения задач того или иного вида обеспечивают благоприятные условия для сопоставления, сравнения, противопоставления задач, сходных в том или ином отношении, а также для рассмотрения взаимообратных задач. При таком подходе дети с самого начала приучаются проводить анализ задачи, устанавливая связь между данными и искомым, и осознанно выбирать правильное действие для её решения. Решение некоторых задач основано на моделировании описанных в них взаимосвязей между данными и искомым.
При решении текстовых задач используется и совершенствуется знание основных математических понятий, отношений, взаимосвязей и закономерностей. Работа с текстовыми задачами способствует осознанию смысла арифметических действий и математических отношений, пониманию взаимосвязи между компонентами и результатами действий, осознанному использованию действий.
Программой предусмотрено целенаправленное формирование совокупности умений работать с информацией. Эти умения формируются как на уроках, так и во внеурочной деятельности — на факультативных и кружковых занятиях. Освоение содержания курса связано не только с поиском, обработкой, представлением новой информации, но и с созданием информационных объектов: стенгазет, книг, справочников. Новые информационные объекты создаются в основном в рамках проектной деятельности. Проектная деятельность позволяет закрепить, расширить и углубить полученные на уроках знания, создаёт условия для творческого развития детей, формирования позитивной самооценки, навыков совместной деятельности с взрослыми и сверстниками, умений сотрудничать друг с другом, совместно планировать свои действия и реализовывать планы, вести поиск и систематизировать нужную информацию.
Большое внимание в программе уделяется формированию умений сравнивать математические объекты (числа, числовые выражения, различные величины, геометрические фигуры и т. д.), выделять их существенные признаки и свойства, проводить на этой основе классификацию, анализировать различные задачи, моделировать процессы и ситуации, отражающие смысл арифметических действий, а также отношения и взаимосвязи между величинами, формулировать выводы, делать обобщения, переносить освоенные способы действий в изменённые условия.
Знание и понимание математических отношений и взаимозависимостей между различными объектами (соотношение целого и части, пропорциональные зависимости величин, взаимное расположение объектов в пространстве и др.), их обобщение и распространение на расширенную область приложений выступают как средство познания закономерностей, происходящих в природе и в обществе. Это стимулирует развитие познавательного интереса школьников, стремление к постоянному расширению знаний, совершенствованию освоенных способов действий.
Изучение математики способствует развитию алгоритмического мышления младших школьников. Программа предусматривает формирование умений действовать по предложенному алгоритму, самостоятельно составлять план действий и следовать ему при решении учебных и практических задач, осуществлять поиск нужной информации, дополнять ею решаемую задачу, делать прикидку и оценивать реальность предполагаемого результата. Развитие а лгоритмическо го мышлени я послужит базой для успешного овладения компьютерной грамотностью.
В процессе освоения программного материала младшие школьники знакомятся с языком математики, осваивают некоторые математические термины, учатся читать математический текст, высказывать суждения с использованием математических терминов и понятий, задавать вопросы по ходу выполнения задани й , обосновывать правильность выполненных действий, характеризовать результаты своего учебного труда и свои достижения в изучении этого предмета.
Овладение математическим языком, усвоение алгоритмов выполнения действий, умения строить планы решения различных задач и прогнозировать результат являются основой для формирования умений рассуждать, обосновывать свою точку зрения, аргументировано подтверждать или опровергать истинность высказанного предположения. Освоение математического содержания создаёт условия для повышения логической культуры и совершенствования коммуникативной деятельности учащихся.
Программа ориентирована на формирование умений использовать полученные знания для самостоятельного поиска новых знаний, для решения задач, возникающих в процессе различных видов деятельности, в том числе и в ходе изучения других школьных дисциплин.
Математические знания и представления о числах, величинах,
геометрических фигурах лежат в основе формирования общей картины мира и познания законов его развития. Именно эти знания и представления необходимы для целостного восприятия объектов и явлений природы, многочисленных памятников культуры, сокровищ искусства.
Обучение младших школьников математике на основе данной программы способствует развитию и совершенствованию основных познавательных процессов (включая воображение и мышление, память и речь). Дети научатся не только самостоятельно решать поставленные задачи математическими способами, но и описывать на языке математики выполненные действия и их результаты, планировать, контролировать и оценивать способы действий и сами действия, делать выводы и обобщения, доказывать их правильность. Освоение курса обеспечивает развитие творческих способностей, формирует интерес к математическим знаниям и потребность в их расширении, способствует продвижению учащихся начальных классов в познании окружающего мира.
Содержание курса имеет концентрическое строение, отражающее последовательное расширение области чисел. Такая структура позволяет соблюдать необходимую постепенность в нарастании сложности учебного материала, создаёт хорошие условия для углубления формируемых знаний, отработки умений и навыков, для увеличения степени самостоятельности (при освоении новых знаний, проведении обобщений, формулировании выводов), для постоянного совершенствования универсальных учебных действий.
Структура содержания определяет такую последовательность изучения учебного материала, которая обеспечивает не только формирование осознанных и прочных, во многих случаях доведённых до автоматизма навыков вычислений, но и доступное для младших школьников обобщение учебного материала, понимание общих принципов и законов, лежащих в основе изучаемых математических фактов, осознание связей между рассматриваемыми явлениями. Сближенное во времени изучение связанных между собой понятий, действий, задач даёт возможность сопоставлять, сравнивать, противопоставлять их в учебном процессе, выявлять сходства и различия в рассматриваемых фактах.
Место курса в учебном плане
На изучение математики в каждом классе начальной школы отводится по 4 ч в неделю. Курс рассчитан на 540 ч: в 1 классе — 4 часа в неделю, 132 ч (33 учебные недели), во 2-4 классах – по 4 часа в неделю, 136 ч (34 учебные недели). Увеличение количества часов по данному курсу осуществлено за счёт школьного компонента во 2 классах — 1 час в неделю (34 часа), 3 классе – 1 час в неделю (34 часа), в 4 классах — 1 час в неделю (34 часа).
Количество часов в неделю
Количество учебных недель
Источник: nsportal.ru
По программам М.И. Моро и др., Н.Б. Истоминой
К алгебраическим понятиям, которые изучают в начальных классах, относят: числовые и буквенные выражения, числовые равенства и неравенства, уравнения.
Этот материал включен в курс математики с целью:
1) более осознанного усвоения математических понятий;
2) для установления преемственности с курсом математики в средней школе.
С начала 1 класса учащихся знакомят с понятиями: числовое выражение, равенство и неравенство.
Числовым выражением называют запись, состоящую из чисел, знаков действий и скобок. Например, 2+(6+4).
Числовым равенством называют запись, состоящую из чисел, знаков действий и знака равно (или: два выражения, соединенные знаком = называют равенством). Например, 2+5=3+4.
Два выражения, соединенные знаками «больше» или «меньше» называют числовым неравенством. Например, 7+5
Число, получаемое в результате выполнения всех действий в числовом выражении, называют значением числового выражения.
Если числовое значение найти нельзя, то говорят, что числовое выражение не имеет смысла. Например, 23: (12-12).
В начальных классах, т.к. изучают действия только с целыми положительными числами, к выражениям, не имеющим смысл, относят и такие (4 — 11).
С начала 1 класса вводят простейшие числовые выражения в одно действие, постепенно количество действий увеличивают. При этом, т.к. это только сложение и вычитание, то сообщают, что все действия надо выполнять по очереди: слева направо, независимо сложение это или вычитание.
(М1М ч.2 стр.7)
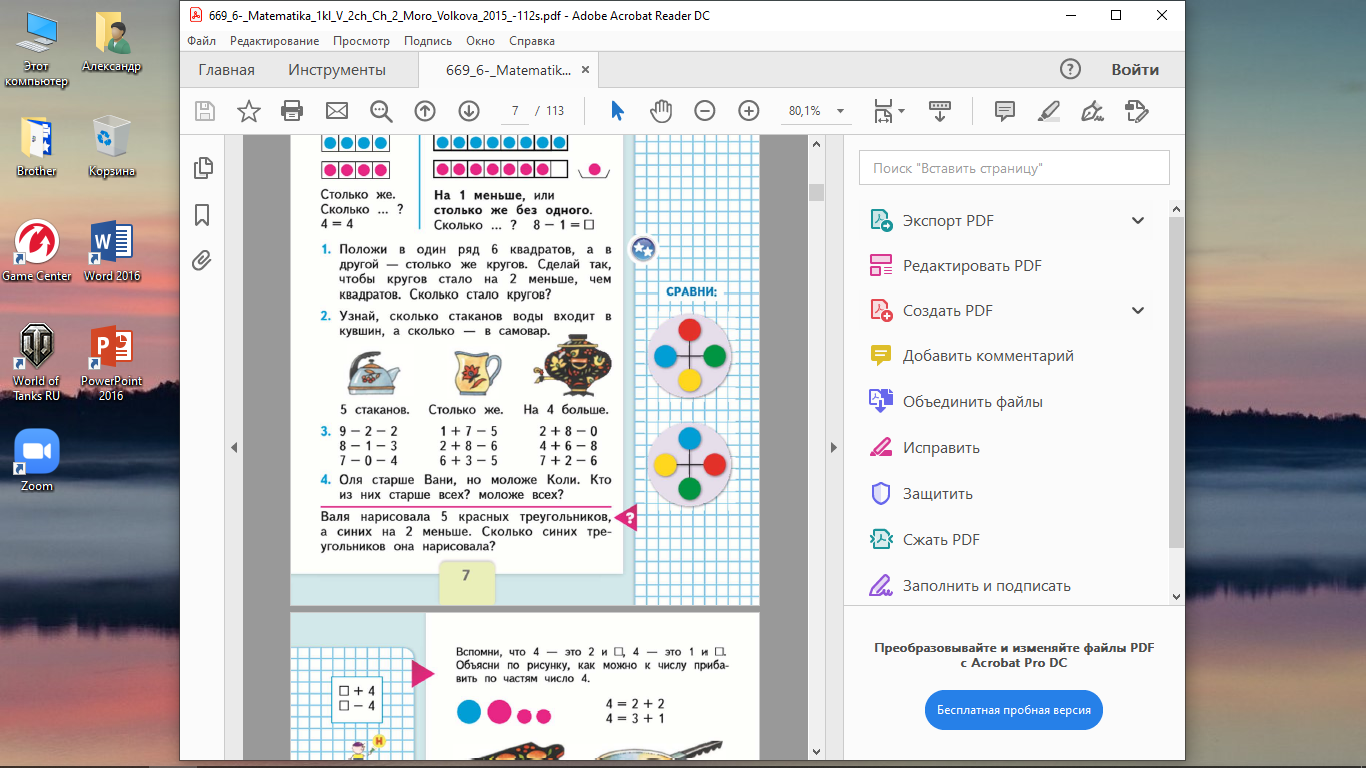
Кроме числовых, изучают буквенные выражения, равенства и неравенства.
Буквенным называют выражение, содержащее букву.
Смысл буквы двоякий, с одной стороны – это неизвестное число, но с другой стороны – переменная величина.
При введении буквенных выражений можно использовать такую методику. На подготовительном этапе рассматривается выражение с «окошками». На уроке введения также берем такое выражение с «окошками», например, 10+ . Рассуждаем, какое число можно поставить в «окошко»? Здесь можно использовать специальное наглядное пособие – абак с движущейся лентой.
Учитель передвигает ленту и последовательно получает несколько числовых выражений, каждый раз находим значение нового выражения и приходим к выводу, что вместо «окошка» можно поставить любое число и при этом значение выражения будет меняться. Далее предлагают взять это же выражение с «окошком», но поменять его форму. Например, 10+Օ, 10+∆.
Рассуждаем, влияет ли форма окошка на то, какие числа будем подставлять и на значение числового выражения (нет). Следовательно, в данном случае «окошко» — знак, обозначающий, что второе слагаемое неизвестно.
Далее идет ознакомление с буквенным выражением.
(М2Мч.1 с.76)

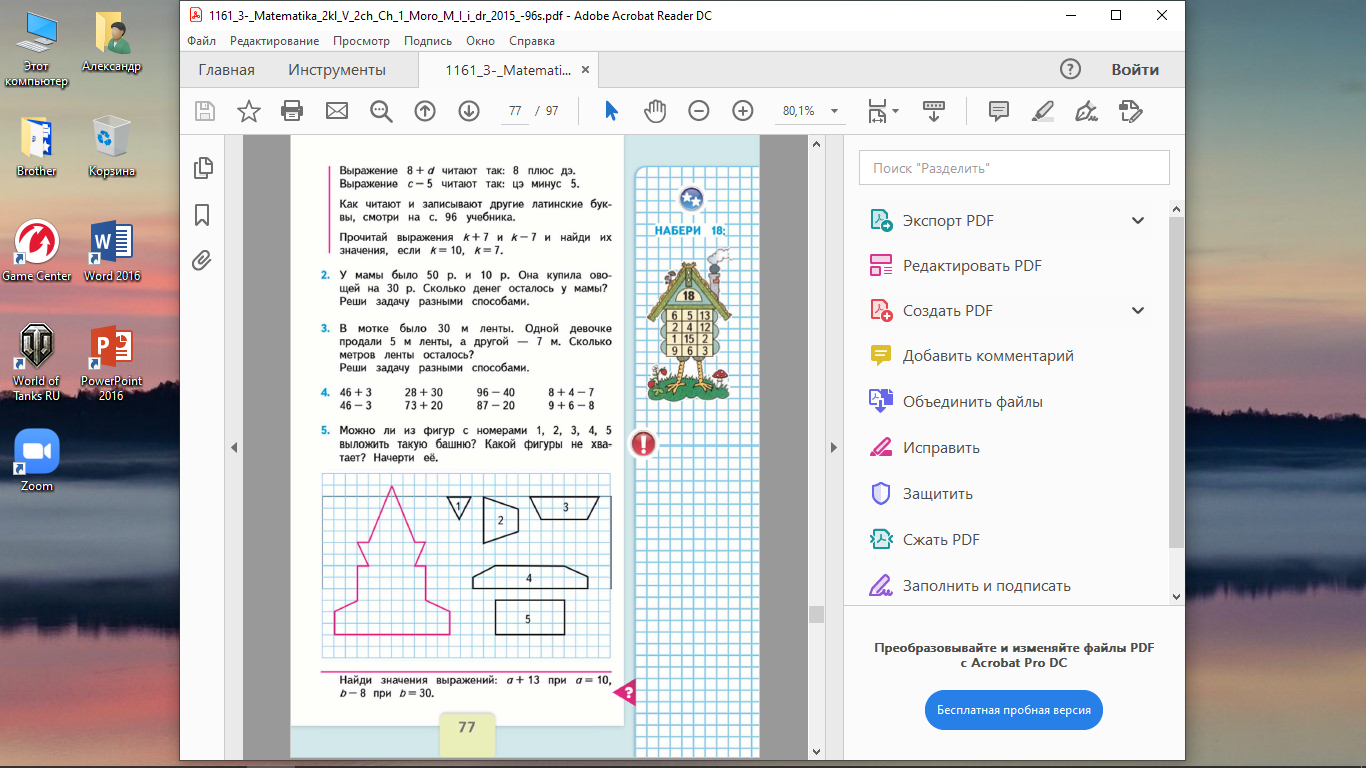
Сообщаем, что в математике для обозначения неизвестного числа используют буквы латинского алфавита, можно вывесить таблицу с латинским алфавитом или записать на доске несколько таких букв (обычно а, b, с, d).
В соответствии со стандартом начальной математической подготовки должны рассматривать только простейшие буквенные выражения, содержащие одну букву. Например, а+5, 8•с. Позднее в 3-4 классах рассматривают буквенные выражения, содержащие две буквы в 1-3 действия. а:3+в:2
Для закрепления предлагают такие упражнения.
1. Найдите значение буквенного выражения при следующих значениях буквы. Например, 8 – b, при b=2,3,4.
2. Самостоятельно подберите несколько значений буквы и найдите значение буквенного выражения. Например, 8 – b. В этом случае обсуждаем, что b не может быть больше 8.
3. Часто в этом случае используется таблица.
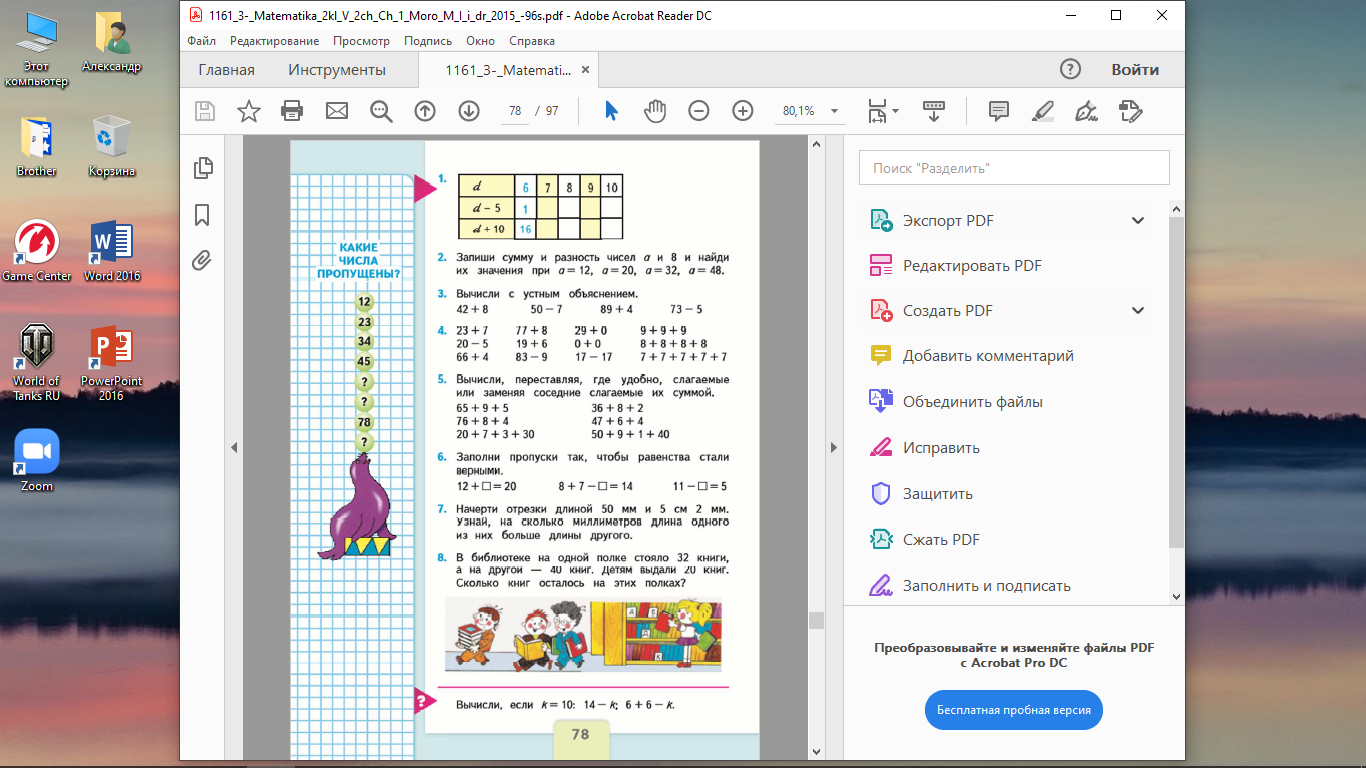
Такие упражнения способствуют не только формированию вычислительных навыков, но и функциональной пропедевтике, т.к. уже в этот период учитель обсуждает с детьми значение переменной величины и функции, хотя термин «функция» не вводится. Учитель показывает, как зависит значение от буквенного выражения, от значения переменных.
Особое внимание в начальных классах уделяют решению уравнений, хотя решение уравнений является основным лишь в средней школе. В начальной школе осуществляется первичное ознакомление с уравнениями и способами их решения. По программе М.И. Моро – во 2 классе ч.1 с.80.

Дети выполняют разнообразные упражнения
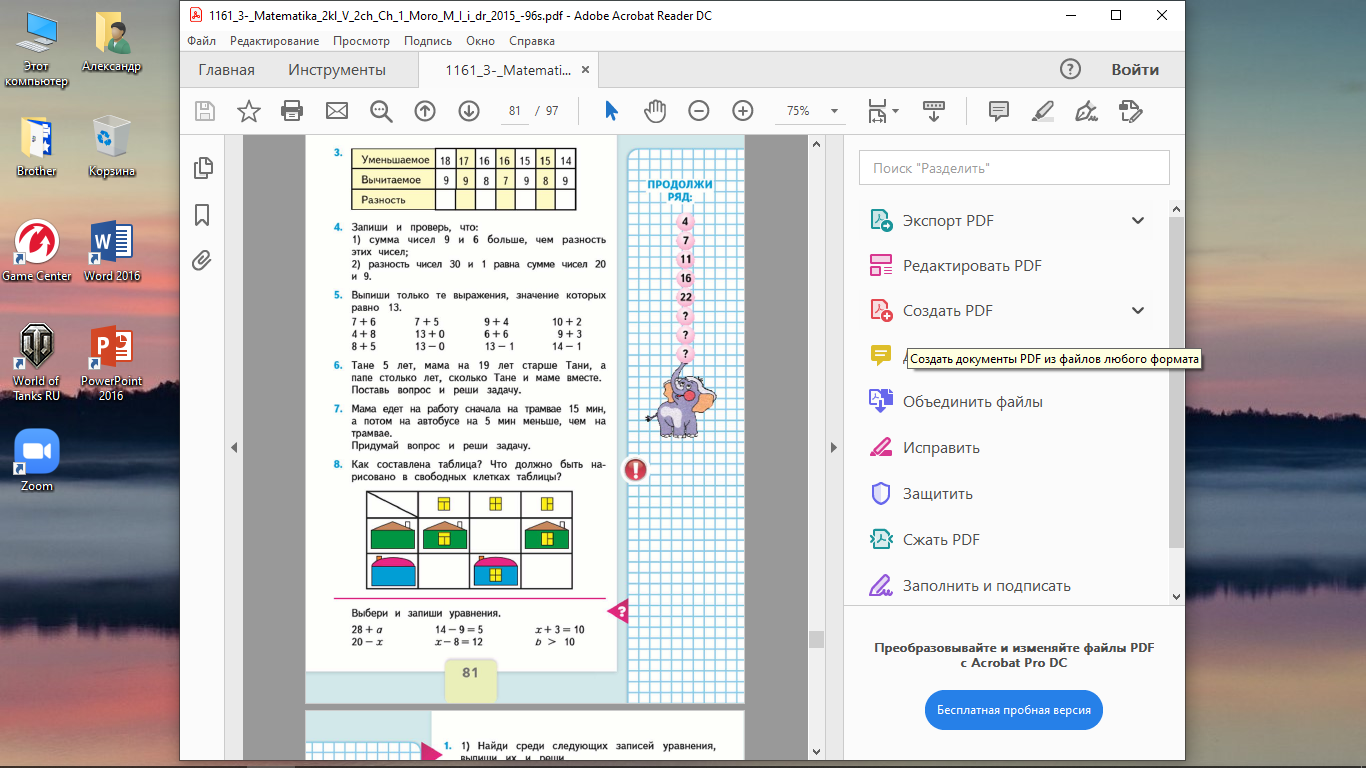


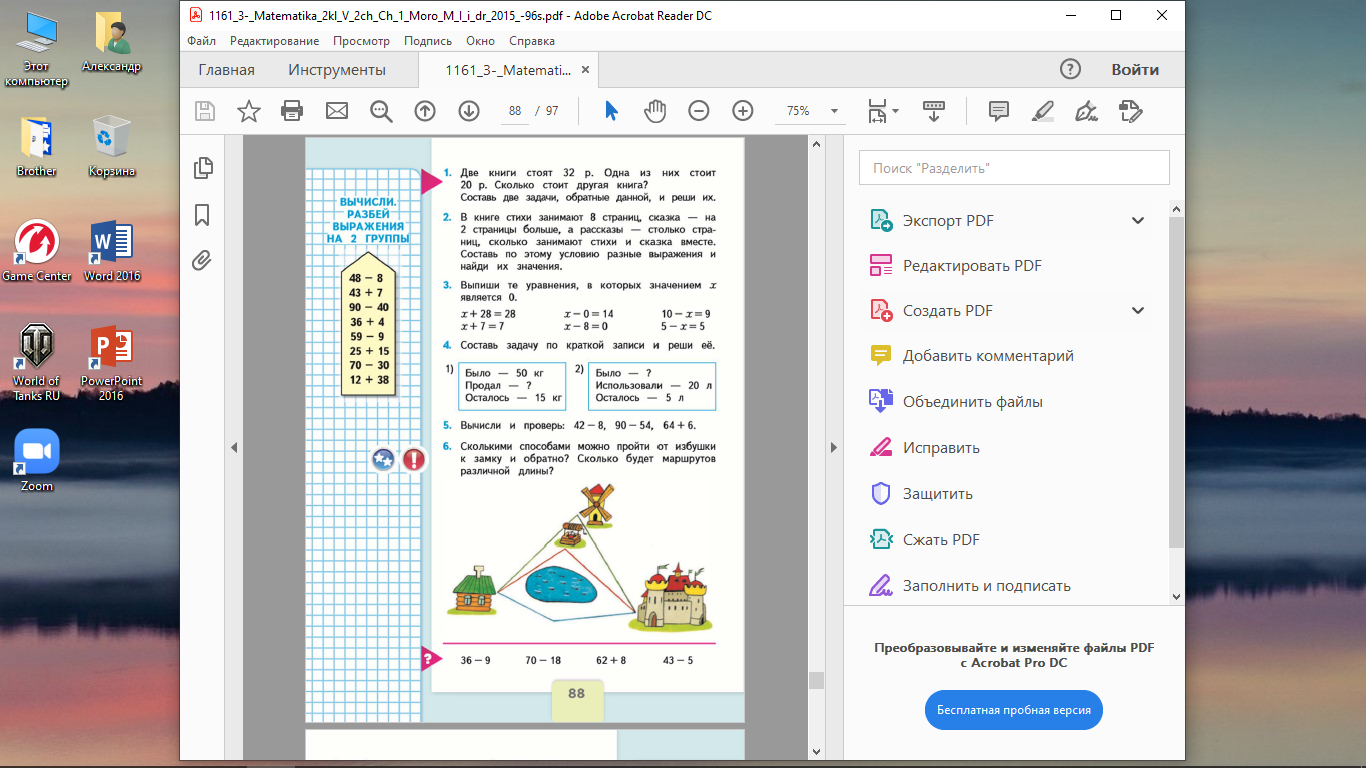
К концу 2 класса начинают изучать «Действия умножения (М2М ч.2 с.48) и деления (М2М ч.2 с.58)», но выражения, в которых есть действия разных ступеней (1 ступень – сложение и вычитание, 2 ступень – умножение и деление) дают только такие, в которых порядок действий «слева направо» будет верным.
Выражения с другим порядком действий появляются лишь в 3 классе при изучении темы «Порядок действий в выражениях». (М3М ч.1 с.24)
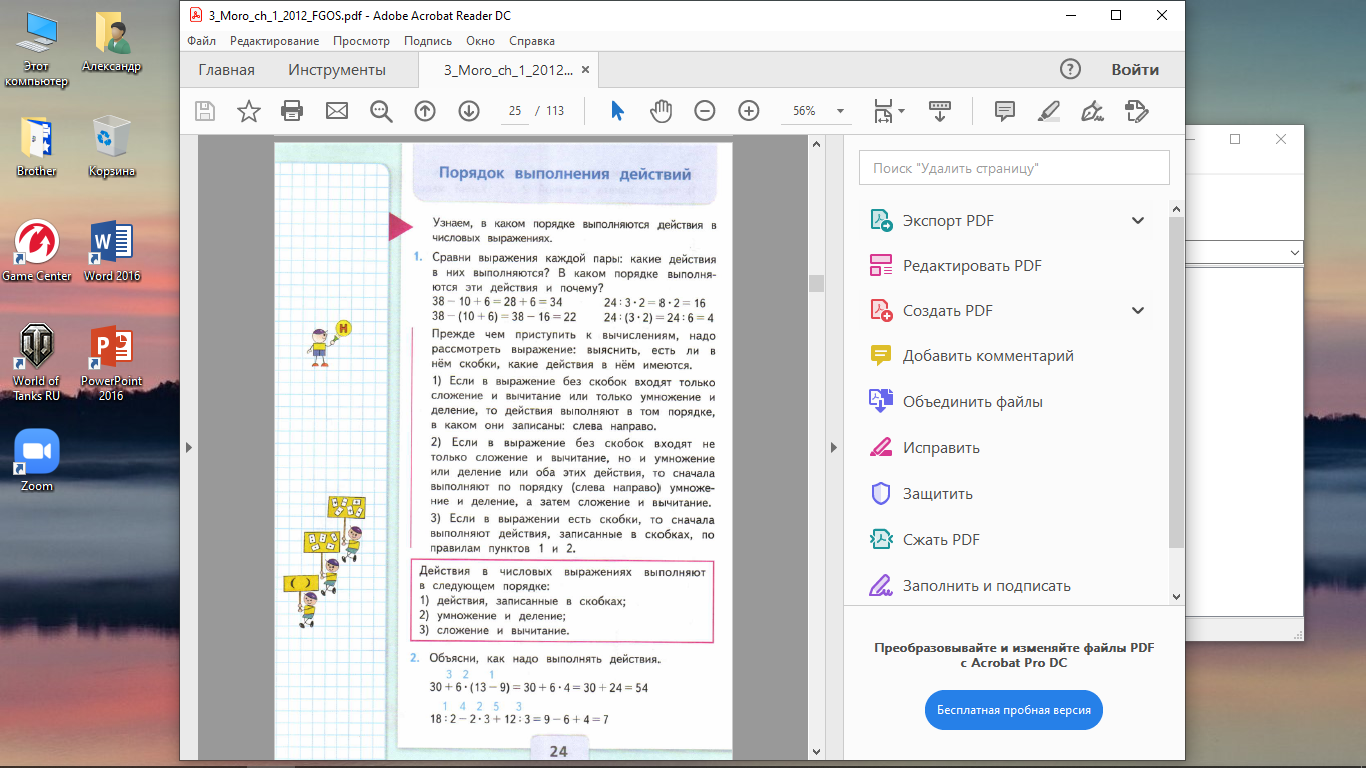
В этой теме по всем программам изучают 3 правила.
Правило 1. Отражает порядок действий в выражениях, содержащих действия одной ступени (сложения и вычитания или умножения и деления). В этом случае действия выполняют по очереди слева направо.
Правило 2. Отражает порядок действий в выражениях, содержащих действия двух ступеней, в этом случае сначала по очереди слева направо выполняют действия 2 ступени, потом действия 1 ступени.
Правило 3. Отражает порядок действий в выражениях со скобками и говорит о том, что действия в скобках надо выполнять в первую очередь. Скобки по всем программам вводят перед изучением сочетательного свойства сложения.
Перед введением скобок можно создать проблемную ситуацию, предложив такое выражение: из 10 вычесть сумму 3 и 2. Пока дети не знают знака «скобки», они запишут без скобок и, следовательно, изменится порядок действий и значение выражений.
Сравним результат, который получился при устном выполнении и при записи. Видим противоречие. Учитель сообщает, что в математике есть специальный знак, показывающий, что это действие надо выполнить в первую очередь. (Найти в учебниках правила выполнения порядка действий).
Среди упражнений, связанных с формированием понятий «числовое выражение», «значение числового выражения» ведущее место принадлежит тем, в которых надо найти значение числового выражения. Этот процесс связан с тождественными преобразованиями числовых выражений, т.е. заменой одного числового выражения другим, тождественно равным ему.
В начальных классах эта терминология не вводится, хотя идентичные преобразования выполняются. В начальных классах их выполняют на основе:
1) правил порядка действий в выражениях;
2) использования свойств действий. Например, (5+2)+3=5+(2+3);
3) вычислительных приемов. Например, 15•3=(10+5)•3=10•3+5•3=30+15=45.
Таким образом, к концу 4 класса, учащиеся должны уметь находить значение числовых выражений в несколько действий (4-6 действий).
Источник: cyberpedia.su