Anova что за программа

Дисперсионный анализ (ANOVA) — это статистический метод, который используется для сравнения средних значений двух или более выборок. Он позволяет определить, различаются ли средние значения между группами, или же различия случайны. ANOVA используется в различных областях, включая науку, инженерию, медицину, социологию и многие другие, где необходимо доказать связь между переменными.

ANOVA является мощным инструментом, который может использоваться в статистическом анализе для оценки влияния исследуемого фактора на зависимую переменную. Это помогает установить, является ли фактор значимым, и позволяет идентифицировать взаимодействие между переменными. ANOVA также позволяет определить, насколько сильно различия между группами, что может быть полезно при выборе стратегий манипулирования факторами.

Правильное применение ANOVA может доставить большую пользу и сделать исследование намного более информативным.

ANOVA дисперсионный анализ STATISTICA #05 | СТАТИСТИКА STATISTICA

Теория дисперсионного анализа

ANOVA может быть использован для различных целей, например, для сравнения средних значений для разных групп или для проверки влияния факторов на исходы. Для проведения ANOVA необходимо определить несколько гипотез:

Нулевая гипотеза — это гипотеза, согласно которой никаких статистически значимых различий между группами не существует. В контексте дисперсионного анализа (ANOVA) она утверждает, что средние значения всех групп равны между собой.

Например, при проведении исследования по сравнению среднего уровня дохода людей в разных группах (например, по возрасту или образованию) нулевая гипотеза будет звучать так: «Средний уровень дохода во всех группах одинаков».

Установление нулевой гипотезы является важным шагом в проведении статистического тестирования, поскольку это позволяет определить статистическую значимость различий между группами. Если результаты тестирования указывают на то, что нулевую гипотезу можно отвергнуть, то это говорит о том, что существует статистически значимое различие между группами.

Нулевая гипотеза может быть отвергнута при помощи статистических инструментов, таких как p-значение, которое оценивает вероятность того, что различия между группами являются случайными. Чем меньше p-значение, тем больше вероятность того, что нулевая гипотеза является ложной и существуют статистически значимые различия между группами. Обычно, если p-значение меньше 0,05, то нулевая гипотеза считается отвергнутой.

Альтернативная гипотеза — это гипотеза, которая предполагает, что статистически значимые различия между группами существуют. В контексте дисперсионного анализа (ANOVA), альтернативная гипотеза утверждает, что хотя бы одно из средних значений групп отличается от среднего значения других групп.

Важно отметить, что нулевая гипотеза всегда предполагается исходной (default hypothesis), и ее опровержение ставит вопрос об альтернативной гипотезе. Поэтому при проведении дисперсионного анализа, рассматриваемые гипотезы обычно выглядят так: «Нулевая гипотеза: средние значения всех групп равны между собой.» и «Альтернативная гипотеза: хотя бы одно из средних значений групп отличается от среднего значения других групп.»

ANOVA дисперсионный анализ | АНАЛИЗ ДАННЫХ #9

Нулевая и альтернативная гипотезы в ANOVA используются для оценки различий между группами и определения статистической значимости этих различий. Результаты теста ANOVA могут помочь исследователям выявить факторы, влияющие на исходы исследования. Если нулевая гипотеза была отвергнута, то это означает, что между группами есть статистически значимые различия, и изучение этих различий может помочь исследователям понять, какой фактор оказывает наибольшее влияние на исходы.

ANOVA использует три типа дисперсии: межгрупповая дисперсия, внутригрупповая дисперсия и общая дисперсия. Межгрупповая дисперсия представляет различия между средними значениями групп, внутригрупповая дисперсия представляет изменчивость внутри каждой группы, а общая дисперсия — это сумма межгрупповой и внутригрупповой дисперсий.

Для проведения ANOVA существует несколько типов тестов, каждый из которых может быть использован в зависимости от типа данных и количества групп. Например, однофакторный дисперсионный анализ используется для сравнения средних значений при одном факторе, а двухфакторный дисперсионный анализ используется для сравнения средних значений при двух или более факторах.

Типы ANOVA

1. Однофакторный ANOVA (однофакторный дисперсионный анализ) – это метод статистического анализа данных, который используется для определения наличия статистически значимых различий между двумя или более группами по одной независимой переменной. Данный метод широко используется в научных исследованиях, маркетинговых исследованиях и других областях, где необходимо определить различия между двумя или более группами объектов или явлений. Входными данными для однофакторного ANOVA являются значения зависимой переменной и групповой фактор, на основе которых проводится анализ. Фактор может быть любой номинальной или порядковой переменной, которая разделяет выборку на группы (в простом случае, это может быть пол, возраст, уровень образования и т.д.). Зависимая переменная – это та переменная, которую мы хотим сравнить в различных группах. Однофакторный ANOVA проверяет нулевую гипотезу о том, что среднее значение зависимой переменной одинаково во всех группах. Если p-значение меньше заданного уровня значимости (обычно 0.05), тогда мы можем сделать вывод о том, что средние значения по группам различаются статистически значимо друг от друга. Кроме того, однофакторный ANOVA дает множество других статистических показателей, включая среднее значение, стандартное отклонение, диапазон, размах, медиану, аномальные значения и т.д. В качестве дополнительного анализа для определения различий между группами могут быть использованы такие методы, как Т-тест, АНКОВА и другие. Однофакторный ANOVA является базовым методом анализа для исследования факторов, которые влияют на зависимые переменные в различных группах. Использование этого метода помогает объективно оценивать результаты и достоверно определять, какие факторы играют ключевую роль в исследуемом явлении или процессе.
2. Двухфакторный ANOVA (двухфакторный дисперсионный анализ) – это метод статистического анализа данных, который позволяет определить наличие статистически значимых различий между группами по двум независимым переменным (факторам). Такой подход позволяет оценить влияние каждой независимой переменной на зависимую переменную, а также выявить возможное взаимодействие между факторами. В случае значимых различий, производится дополнительный анализ, чтобы установить, между какими группами существуют различия.
3. Многовариантный ANOVA (analysis of variance) — это статистический метод, который используется для анализа различий между группами (факторами) и влияния различных переменных (факторов) на исследуемую зависимую переменную. Он позволяет выявить, есть ли статистически значимое влияние одного или нескольких факторов на зависимую переменную, и определить, какие из факторов оказывают наибольшее влияние. Многовариантный ANOVA может использоваться для анализа различных типов данных, включая непрерывные, дискретные и категориальные переменные. Он также может рассчитываться для различных уровней взаимодействия между факторами, что позволяет учитывать сложные взаимодействия между переменными. Основная идея многовариантного ANOVA заключается в том, что общее количество изменений в зависимой переменной разделяется на две части: изменения, связанные с факторами, и изменения, которые не могут быть объяснены факторами (остаток). Факторы могут быть любого типа, но обычно они бывают двух типов: факторы, которые могут быть контролируемыми или экспериментальными (например, воздействие на здоровье человека разных типов диет), и факторы, которые являются неконтролируемыми или наблюдаемыми (например, пол, возраст, образование). Метод многовариантного ANOVA может быть выполнен в несколько шагов. Сначала нужно провести анализ на уровне каждого фактора (унимодальный анализ — one-way ANOVA). Затем производится многовариантный анализ, который позволяет оценить влияние всех факторов на зависимую переменную одновременно. Для этого используется многовариантный тестовый показатель F-статистики. Многовариантный ANOVA также может использоваться для оценки взаимодействия между факторами, например, могут ли переменные влиять друг на друга или быть нелинейными. Для этого используется двуфакторный или трехфакторный ANOVA, в котором изучается влияние нескольких факторов на зависимую переменную. Многовариантный ANOVA является полезным инструментом для исследования дисперсии и определения значимости факторов в зависимой переменной. Он также может использоваться в более сложных исследованиях, таких как оценка взаимодействия между группами и изучения различных факторов, влияющих на зависимую переменную.

Шаги проведения ANOVA

1. Определение гипотезы — это основной шаг, который необходимо проделать перед проведением ANOVA. Гипотеза должна содержать утверждение о том, что средние значения переменной одинаковы в нескольких группах. Например, предположим, что мы хотим узнать, есть ли статистически значимые различия в среднем росте людей в трех группах: мужчинах, женщинах и детях. Тогда нулевая гипотеза будет состоять в том, что средний рост одинаков во всех трех группах. Альтернативная гипотеза будет заключаться в том, что средний рост отличается в двух или более группах. Нулевая гипотеза всегда формулируется таким образом, что она может быть отвергнута на основе статистических данных. Например, если p-value меньше выбранного уровня значимости, то можно отбросить нулевую гипотезу и предположить, что существуют различия между группами. Важно, чтобы гипотеза была четкой и такой, которую можно проверить с помощью статистических данных. В противном случае, проведение ANOVA становится бессмысленным.
2. Сбор данных — это следующий шаг после определения гипотезы, который необходимо выполнить перед проведением ANOVA. Для сбора данных нужно определить, какие переменные изучаются, какие группы данных будут сравниваться и какой размер выборки необходим. Выбор уровня значимости — это важный шаг ANOVA, который определяет вероятность того, что различия между группами являются случайными. Обычно уровень значимости принимается равным 0,05 (5%), что означает, что различия между группами, имеющие вероятность меньше 5%, считаются статистически значимыми. Выбор правильного уровня значимости очень важен, так как неправильно выбранный уровень значимости может привести к неверным выводам. Если уровень значимости выбран слишком высоким, то могут быть найдены статистически значимые различия, которых на самом деле нет. Если уровень значимости слишком низкий, то могут быть пропущены настоящие статистически значимые различия. Правильный выбор уровня значимости зависит от цели исследования, характеристик групп и размеров выборки. Этот выбор должен быть продуманным и основываться на знаниях и опыте в данной области.
3. Определение степеней свободы и критических значений: степени свободы — это количество наблюдений, которые могут быть свободно изменены в каждой группе данных. Критическое значение — это значение, при котором различия между группами становятся статистически значимыми.
4. После сбора данных и выбора уровня значимости необходимо рассчитать статистические показатели для проведения ANOVA. Статистические показатели, которые используются в ANOVA — это F-статистика и p-value. F-статистика (F-значение) измеряет различия между группами, то есть отношение между средними значениями в группах и дисперсией внутри групп. Если F-значение большое, то это указывает на статистически значимые различия между группами. p-value (вероятность) — это вероятность того, что различия между группами были случайными и не связаны с фактором, который изучается. Если p-value меньше выбранного уровня значимости, то можно отбросить нулевую гипотезу и утверждать, что между группами есть статистически значимые различия. Важно знать, что F-статистика и p-value не являются самостоятельными критериями для определения статистической значимости. Они должны использоваться вместе с другими статистическими методами для получения более точных результатов.
5. Оценка результатов и интерпретация полученных данных: после проведения ANOVA необходимо проанализировать полученные результаты. Если значение p-value меньше уровня значимости, то можно отбросить нулевую гипотезу и утверждать, что между группами есть статистически значимые различия. Интерпретируя эти различия, можно выйти на конкретный вывод, касающийся фактора, который изучается.

Пример применения ANOVA

Представим, что у нашего интернет-магазина есть три различных дизайна для главной страницы сайта, и мы хотим определить, какой из них наиболее эффективен в увеличении количества продаж. В этом случае мы можем провести эксперимент, в котором будут участвовать три группы покупателей, каждой группе будет показан только один из дизайнов главной страницы.

Для начала, мы должны определить, сколько покупателей нужно включить в каждую группу. Чтобы определить размер каждой группы, мы можем использовать статистические методы для расчета минимального размера выборки. Допустим, мы решили, что каждая группа должна состоять из 1000 покупателей.

Для этого эксперимента мы должны также определить, какие метрики будут измеряться. Для нашего примера мы будем измерять среднее количество продаж на каждого покупателя в каждой группе.

Когда эксперимент будет завершен, мы будем иметь данные о количестве продаж для каждой группы. Мы можем использовать ANOVA для анализа данных и определения, есть ли значимые различия между группами.

Перед проведением анализа необходимо проверить данные на нормальность распределения и выполнить другие необходимые условия для проведения анализа.

После проведения ANOVA мы получаем статистические показатели, такие как F-значение и p-значение. F-значение показывает различия между средними значениями групп, а p-значение показывает статистическую значимость различий между группами. Если p-значение меньше заданного уровня значимости (обычно 0,05), то мы можем сделать вывод о наличии значимых различий между группами.

Например, если мы получили F-значение 3,5 и p-значение 0,02, то мы можем сделать вывод о наличии статистически значимых различий между группами. Это означает, что один дизайн главной страницы сильнее влияет на увеличение продаж, чем другие.

Дополнительно, если у нас есть статистически значимые различия между группами, мы можем провести дополнительный анализ, например, сравнение каждой группы с другой с помощью теста Тюрки или Холма, чтобы определить, где именно находятся различия. Также мы можем рассмотреть другие важные метрики, такие как время проведения эксперимента и влияние внешних факторов на продажи. Важно понимать, что ANOVA — это только инструмент, который помогает нам делать выводы на основе данных. Поэтому проведение эксперимента должно быть тщательно спланировано и осуществлено в соответствии с научными методами для того, чтобы результаты были надежными и полезными для бизнеса.

Заключение

ANOVA очень важен для статистического анализа данных и исследований. Этот метод позволяет определить, какие факторы влияют на изменения в группах и имеет множество применений.

Рекомендации по применению ANOVA:

1. Необходимо тщательно выбирать данные для анализа и проверять их на соответствие критериям ANOVA.
2. Всегда проводите тесты на нормальность, чтобы проверить, являются ли данные нормально распределенными.
3. При использовании ANOVA следует учитывать влияние других факторов, которые не связаны с переменной, которую вы исследуете.
4. Помните, что ANOVA рассчитывает только показатели среднего значения, поэтому может не учитывать взаимодействие между переменными.
5. Всегда проверяйте статистическую значимость результата ANOVA и учитывайте размер выборки и разброс данных.
6. Используйте ANOVA для сравнения трех или более групп, но не забывайте о других методах анализа, таких как t-тест, если вы хотите сравнить всего две группы.
7. Наконец, не забывайте, что результаты ANOVA могут быть интерпретированы по-разному и, если это возможно, используйте другие методы анализа для проверки ваших выводов.

В целом, ANOVA является мощным методом статистического анализа, который можно использовать для исследования различий между группами. Он помогает находить значимые различия и определить факторы, влияющие на результаты исследования. Однако, для более точных результатов, необходимо учитывать все факторы влияния и применять другие методы анализа, если это необходимо.

В завершение хочу порекомендовать бесплатный вебинар от OTUS, где преподаватели покажут как настроить мониторинг PostgreSQL с помощью grafana и Prometheus.

• дисперсионный анализ
• анализ данных
• anova
• статический анализ

Источник: habr.com

Тесты — ANOVA на C#

Дисперсионный анализ (analysis of variance, ANOVA) — классический статистический метод, применяемый для заключения о том, являются ли средние трех или более групп равными, в ситуациях, где в наличии только одна выборка данных. Например, в университете есть три разных вводных курса в компьютерную науку. Каждый курс ведет один и тот же преподаватель, но использует другой учебник и другую методику преподавания. Вы хотите узнать, одинакова ли академическая успеваемость студентов.

Вы проводите экзамен, в ходе которого оцениваете подготовку в области компьютерной науки по шкале от 1 до 15, но, поскольку этот экзамен очень дорогостоящий и занимающий много времени, вы можете проэкзаменовать лишь шесть случайным образом выбранных студентов с каждого курса. Вы ведете экзамен и выполняете ANOVA на выборках, чтобы сделать заключение, являются ли средние оценки по всем трем курсам одинаковыми.

Если вы новичок в ANOVA, название этого метода может слегка сбить с толку, так как его цель — анализ средних значений наборов данных. ANOVA назван так потому, что закулисно он анализирует дисперсии (variances) для логических заключений о средних.

Хороший способ получить представление о том, что такое ANOVA и куда я клоню в этой статье, — взглянуть на демонстрационную программу на рис. 1. В демонстрации подготавливаются «зашитые» в код оценки для трех групп. Заметьте, что в Group1 только четыре оценки, а в Group3 — пять. Размеры выборок весьма часто неравные, поскольку испытуемые объекты могут выпадать либо данные могут быть утрачены или повреждены.

Рис. 1. Демонстрация ANOVA на C#

В ANOVA две главные стадии. На первой вычисляются F-статистическое значение (критерий Фишера) и пара значений, называемых степенями свободы (degrees of freedom, df), используя данные выборки. На второй стадии на основе значений F и df определяется вероятность того, что все популяционные средние (population means) одинаковы (p-значение). Первая стадия сравнительно несложна, а вторая очень трудна.

В демонстрации значение F равно 15.884. В целом, чем больше F, тем менее вероятно, что все популяционные средние одинаковы. Вскоре я поясню, почему df = (2, 12). На основе F и df вычисленное p-значение равно 0.000425. Оно очень мало, поэтому вы заключили бы, что популяционные средние скорее всего не одинаковы.

В этот момент вы могли бы выполнить дополнительные статистические проверки, чтобы определить, какие популяционные средние отличаются друг от друга. В случае демонстрационных данных оказывается, что Group1 (среднее выборки = 4.50) хуже Group2 (среднее = 9.67) и Group3 (среднее = 10.60).

Демонстрационная программа

Чтобы создать демонстрационную программу, я запустил Visual Studio, открыл File | New | Project и выбрал шаблон C# Console Application. В этой программе нет значимых зависимостей от .NET Framework, поэтому подойдет любая версия Visual Studio. После загрузки кода шаблона в окно редактора я переименовал в окне Solution Explorer файл Program.cs в более описательный AnovaProgram.cs, и Visual Studio автоматически переименовала класс Program за меня.

В начале кода я удалил все лишние выражения using, оставив только ссылку на пространство имен верхнего уровня System. Общая структура программы показана на рис. 2. Демонстрационная программа слишком длинна, чтобы представить ее здесь во всей полноте, но весь исходный код вы найдете в пакете, сопутствующем этой статье.

Рис. 2. Структура демонстрационной программы

using System; namespace Anova < class AnovaProgram < static void Main(string[] args) < Console.WriteLine(«Begin ANOVA using C# demo»); // Подготавливаем данные выборки. // Используем данные для вычисления F и df. // Используем F и df для вычисления p-значения Console.WriteLine(«End ANOVA demo»); >static double Fstat(double[][] data, out int[] df) < . . >static double LogGamma(double z) < . . >static double BetaIncCf(double a, double b, double x) < . . >static double BetaInc(double a, double b, double x) < . . >static double PF(double a, double b, double x) < . . >static double QF(double a, double b, double x) < . . >static void ShowData(double[][] data, string[] colNames) < . . >> >

Статический метод Fstat вычисляет и возвращает F-статистику на основе данных, хранящихся в объекте «массив массивов». Этот метод также вычисляет и возвращает два значения df в выходном параметре-массиве. ShowData — это просто небольшая вспомогательная функция для отображения средних по выборке.

Остальные пять методов используются для вычисления p-значения. QF — основной метод. Он вызывает метод PF, который в свою очередь обращается к методу BetaInc, а тот вызывает методы BetaIncCf и LogGamma.

После некоторых предваряющих сообщений через WriteLine метод Main подготавливает и отображает данные выборок:

double[][] data = new double[3][]; // 3 группы data[0] = new double[] < 3, 4, 6, 5 >; data[1] = new double[] < 8, 12, 9, 11, 10, 8 >; data[2] = new double[] < 13, 9, 11, 8, 12 >; string[] colNames = new string[] < «Group1», «Group2», «Group3» >; ShowData(data, colNames);

В реальном сценарии ваши данные скорее всего хранились бы в текстовом файле, и вы написали бы вспомогательную функцию для чтения и загрузки данных в массив массивов.

F-статистика и df вычисляются так:

int[] df = null; double F = Fstat(data, out df);

В случае ANOVA df для набора данных представляет собой пару значений. Первое является K–1, где K — количество групп, а второе — N–K, где N — общее количество значений в выборке. Поэтому для демонстрационных данных df = (K–1, N–K) = (3–1, 15–3) = (2, 12).

Затем p-значение вычисляется и отображается следующим образом:

double pValue = QF(df[0], df[1], F); Console.Write(«p-value = «);

Итак, при выполнении ANOVA выражения вызовов очень просты. Но за кулисами осуществляется большой объем работы.

Вычисление F-статистики

Вычисление значения F-статистики (критерия Фишера) происходит в несколько этапов. Допустим, значения данных в выборке такие же, как в демонстрации:

Group1: 3.00, 4.00, 6.00, 5.00 Group2: 8.00, 12.00, 9.00, 11.00, 10.00, 8.00 Group3: 13.00, 9.00, 11.00, 8.00, 12.00

Первый этап — вычисление средних для каждой группы и совокупного среднего по всем значениям выборки. В случае демонстрационных данных имеем следующее:

means[0] = (3.0 + 4.0 + 6.0 + 5.0) / 4 = 4.50 means[1] = (8.0 + 12.0 + 9.0 + 11.0 + 10.0 + 8.0) / 6 = 9.67 means[2] = (13.0 + 9.0 + 11.0 + 8.0 + 12.0) / 5 = 10.60 gMean = (3.0 + 4.0 + . . . + 12.0) / 15 = 8.60

Определение метода Fstat начинается с:

static double Fstat(double[][] data, out int[] df) < int K = data.Length; // количество групп int[] n = new int[K]; // число элементов в каждой группе int N = 0; // общее количество точек данных for (int i = 0; i < K; ++i) < n[i] = data[i].Length; N += data[i].Length; >.

К этому моменту локальный массив n содержит количество значений в каждой группе, K — число групп, а N — общее количество значений во всех группах. Затем вычисляются групповые средние (group means) и помещаются в массив means, а вычисленное среднее по совокупности (grand mean) записывается в переменную gMean:

double[] means = new double[K]; double gMean = 0.0; for (int i = 0; i < K; ++i) < for (int j = 0; j < data[i].Length; ++j) < means[i] += data[i][j]; gMean += data[i][j]; >means[i] /= n[i]; > gMean /= N;

Следующий этап — вычисление суммы квадратов между группами (SSb) и среднего квадрата между группами (MSb). SSb — это взвешенная сумма квадратов разностей между средним каждой группы и совокупным средним. MSb = SSb / (K–1), где K — количество групп. В случае демонстрационных данных это выглядит так:

SSb = (4 * (4.50 — 8.60)^2) + (6 * (9.67 — 8.60)^2) + (5 * (10.60 — 8.60)^2) = 94.07 MSb = 94.07 / (3-1) = 47.03

Вот код, вычисляющий SSb и MSb:

double SSb = 0.0; for (int i = 0; i < K; ++i) SSb += n[i] * (means[i] — gMean) * (means[i] — gMean); double MSb = SSb / (K — 1);

Очередной этап — вычисление суммы квадратов внутри групп (SSw) и среднего квадрата внутри групп (MSw). SSw — это сумма квадратов разностей между каждым значением выборки и ее групповым средним. MSw = SSw / (N–K). В случае демонстрационных данных это выглядит так:

SSw = (3.0 — 4.50)^2 + . . + (8.0 — 9.67)^2 + . . + (12.0 — 10.60)^2 = 35.53 MSw = 35.53 / (15-3) = 2.96

Вот код, вычисляющий SSw и MSw:

double SSw = 0.0; for (int i = 0; i < K; ++i) for (int j = 0; j < data[i].Length; ++j) SSw += (data[i][j] — means[i]) * (data[i][j] — means[i]); double MSw = SSw / (N — K);

Последний этап — вычисление двух значений df и F-статистики. Двумя значениями df являются K–1 и N–K. F = MSb / MSw. В случае демонстрационных данных это выглядит так:

df = (K-1, N-K) = (3-1, 15-3) = (2, 12) F = 47.03 / 2.96 = 15.88.

Демонстрационный код, вычисляющий df и F, представляет собой следующее:

. df = new int[2]; df[0] = K — 1; df[1] = N — K; double F = MSb / MSw; return F; > // Fstat

Полагаю, вы согласитесь, что при знании математических уравнений вычислений значений F-статистики и df по набору данных является механистичным и сравнительно простым.

Вычисление p-значения

Преобразование значений F-статистики и df в p-значение, сообщающее вам вероятность того, что все популяционные средние равны на основе данных выборки, которая дает F и df, несложное в принципе, но крайне трудное на практике. Я постараюсь пояснить это как можно короче, не вдаваясь в колоссальное количество деталей, которые потребовали бы огромного объема отдельных разъяснений. Взгляните на график на рис. 3.

Рис. 3. Вычисление p-значения по значениям F-статистики и df

F(x)	F(x)
F-Distribution, df1 = 4, df2 = 12	F-распределение, df1 = 4, df2 = 12
The area under curve from calculated F statistic to +infinity is probability that all means are equal	Область под кривой от вычисленного значения F-статистики до +бесконечности отражает вероятность того, что все средние равны
F-statistic = 2.67	F-статистика = 2.67

Каждая возможная пара значений df определяет график, называемый F-распределением (или распределением отношения дисперсии). Форма F-распределения может меняться в широких пределах в зависимости от значений df. График на рис. 3 показывает F-распределение для df = (4, 12). Я использовал df = (4, 12) вместо df = (2, 12) из демонстрационных данных, потому что форма F-распределения при df = (2, 12) очень атипична..

Общая площадь под любым F-распределением составляет ровно 1.0. Если вам известно значение F-статистики, то p-значение — это площадь под F-распределением от F до +бесконечности. Немного сбивает с толку, что площадь под F-распределением от 0 до F-статистики часто называют PF, а площадь под F-распределением от F-статистики до +бесконечности (представляющей p-значение) — QF. Поскольку общая площадь под распределением равна 1, значит, PF + QF = 1. Оказывается, вычислить PF немного легче, чем QF, поэтому, чтобы найти p-значение (QF), как правило, вычисляют PF, а затем вычитают его из единицы и получают QF.

Вычислить PF чертовски трудно, но, к счастью, уже в течение десятилетий известны волшебные оценочные уравнения. Эти математические уравнения и сотни других вы найдете в знаменитом справочнике Абрамовица (Abramowitz) и Стигана (Stegun) «Handbook of Mathematical Functions». Среди программистов в научных областях эту книгу часто называют просто «AS имеет идентификационный номер.

В демонстрации метод PF на самом деле является не более чем оболочкой метода BetaInc:

static double PF(double a, double b, double x) < double z = (a * x) / (a * x + b); return BetaInc(a / 2, b / 2, z); >

Имя метода BetaInc образовано от сокращения «incomplete Beta» (неполная бета-функция). Метод BetaInc использует уравнения AS даны другие алгоритмы, способные вычислять LogGamma, но аппроксимация Ланцоша, не известная на момент публикации AS под номером 26.5.8.

Заключение

В ANOVA делаются три математических допущения: элементы групп данных математически независимы, наборы популяционных данных распределены нормально (как в гауссовом распределении) и эти наборы имеют равные дисперсии.

Существует несколько способов проверки этих допущений, но интерпретация их результатов является трудной задачей. Проблема заключается в следующем. Крайне маловероятно, что реальные данные имеют одинаковое нормальное распределение и в точности равные дисперсии, хотя ANOVA все равно работает, когда данные имеют несколько отличные дисперсии и небольшие отклонения от нормального распределения. Вывод состоит в том, что чрезвычайно сложно доказать допущения ANOVA, поэтому следует проявлять максимальную консервативность при интерпретации результатов.

ANOVA тесно связана с t-критерием (t-test). Последний определяет, действительно ли популяционные средние ровно двух групп одинаковы в ситуациях, где вы располагаете только данными выборки. Так что, если у вас есть три группы, как в этой демонстрации, то вместо использования ANOVA вы могли бы три проверки по t-критериям, сравнивая группы 1 и 2, группы 1 и 3 и группы 2 и 3. Однако этот подход не рекомендуется, поскольку он вводит так называемую ошибку Type 1 (ложноположительный результат).

Разновидность ANOVA, рассмотренная в этой статье, называется однонаправленной (или однофакторной) ANOVA. Другой метод, двунаправленная ANOVA, используется при наличии двух факторов.

ANOVA основана на вычислении значения F-статистики по набору данных. Существуют другие статистические проверки, в которых применяется F-статистика (критерий Фишера). Например, вы можете использовать F-статистику для логического определения, одинаковы ли дисперсии двух групп данных.

Выражаю благодарность за рецензирование статьи экспертам Microsoft Крису Ли (Chris Lee) и Кирку Олинику (Kirk Olynyk).

Источник: learn.microsoft.com

9.6. Дисперсионный анализ anova в планировании экспериментов

Для определения, является фактор значимым или нет, использу­ется дисперсионный анализ ANOVA (analysis of variance), который применим только к количественным факторам. C помощью него определяются количественные отклонения наблюдений от среднего значения. Если какой-либо фактор не оказывает влияние на отклик, то он является незначимым.

C другой стороны, если фактор влияет на отклик, то его (фактора) количественное значение сравнивают c оценкой изменчивости наблюдения, то есть со стандартной ошибкой. Это делается для исключения эффектов, которые являются не более чем случайной флуктуацией. Неявно в ANOVA используется аддитивная математическая мо­дель, которая определяет компоненты изменения в наблюдениях.

Ее называют статистической моделью. Самая простая статистическая модель: 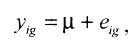т.е. каждое i-e наблюдение представляет собой общее среднее по всем опытам μ, и случайную ошибку eig. B этой модели общее среднее не изменяется от опыта к опыту, в отличие от ошибки.

Статистическая модель для анализа данных экспериментов c од­ним фактором А имеет следующий вид: 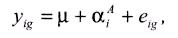где α A i – главный эффект фактора А на уровне i. Все наблюдения на данном уровне обработки анализируются, используя то же самое зна­чение для α A . Так как в этом эксперименте имеется только один фак гор, число комбинаций обработки определяется числом уровней I этого фактора.

Для двух факторов общая модель факторного плана такова: 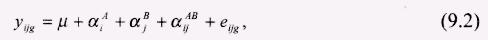где α B j – главный эффект фактора В на уровне j; – взаимодействие фактора А на уровне i и фактора В на уровне j. Сумма эффектов двух факторов не равна сумме их отдельных эффектов из-за взаимодейст­вия между ними.

Главный эффект фактора определяет долю участия фактора в значении функции отклика во время перехода его c нижне­го уровня к верхнему. Дисперсионный анализ, основанный на статистической модели (9.2), заканчивается построением таблицы ANOVA, в которой анали­зируется влияние факторов А, В, взаимодействие между факторами AB и случайные помехи наблюдения.

C помощью ANOVA проверяется гипотеза об отсутствии влия­ния фактора. Если справедлива гипотеза об отсутствии влияния фак­тора, то считается, что все наблюдения получены из одной генераль­ной совокупности. Для проверки гипотезы используется F-распределение Фишера. Критерий Фишера определяет отношение двух выборочных дисперсий.

Если фактор существенно влияет на отклик, то значения F-распределения принимает большие значения и F-cтатистика становится значимой. Таким образом, большие значения F приводят к отбрасыванию гипотезы об отсутствии влияния фактора, т.е. фактор является значимым.

9.7. Библиотечная процедура anova

Библиотечная процедура ANOVA системы GPSS World анали­зирует эксперименты от 1 до 6 факторов, включая взаимодействия 2-го и 3-го порядка между факторами. На рис. 9.3 [19] представлена таблица ANOVA, полученная в GPSS World. Сначала рассмотрим среднюю часть таблицы. Полная сумма квадратов (Total) отделена от компонентов, связанных c эффектами факторов и их взаимодействиями (А, В, AB).

В строке Error (ошибка) приведена остаточная сумма квадратов. Средняя сумма квад­ратов (Mean Square) остаточного члена используется для оценки стан­дартной ошибки эксперимента (в данном случае это величина 2,5). Каждая сумма квадратов делится на число степеней свободы для уровней.

Из статистических соображений степени свободы – это де­литель, который должен использоваться для получения несмещенной оценки стандартной ошибки. Для наших целей, достаточно представ­лять степени свободы как соответствующий делитель, связанный c суммой квадратов в таблице ANOVA. Система GPSS World всегда вычисляет степени свободы.

Каждый фактор и взаимодействие в статистической модели представлены отдельной строкой в верхней части таблицы ANOVA. В каждой строке указана сумма квадратов и число степеней свободы, связанные c оценкой факторов и их взаимодействий. Это – основы, из которых получены другие числа.

Частное от деления определяет средний квадрат ошибки, и в предпоследнем столбце таблицы выда­ется F-статистика для этого эффекта. Сделаем некоторые заключения. Необходимо решить, достаточ­но ли большое значение F-критерия получено для объявления эффек­та значимым.

Пороговое значение, которое используется для сравне­ния, называется «критическим значением F» и помещено справа от F-статистики в той же самой строке. Если полученное значение F пре­вышает критическое значение, то делаем заключение, что имеем дело со значимым эффектом фактора.

Если нет, то считаем, что эффект фактора незначимый и игнорируем любое связанное c ним изменение в наблюдениях, считая, что оно вызвано случайными помехами. Представленная на рис. 9.3 таблица ANOVA показывает, что эффект фактора А значимый, А эффект фактора В и взаимодействие AB незна­чимы.

Иногда при выполнении эксперимента невозможно обнаружить эффект даже в том случае, если он фактически существует. Одна из задач эксперимента заключается в том, чтобы сделать это маловероятным. Из таблицы ANOVA видно, что для получения лучших ре­зультатов необходимо иметь или большую F-статистику или меньшее значение F-критерия.

Желательно удалить часть суммы квадратов ошибки из-за какого-либо важного эффекта, не включенного в ана­лиз. Если это можно сделать, то F-статистика будет больше. Для это­го определяют дополнительные факторы, которые должны быть включены в эксперимент. 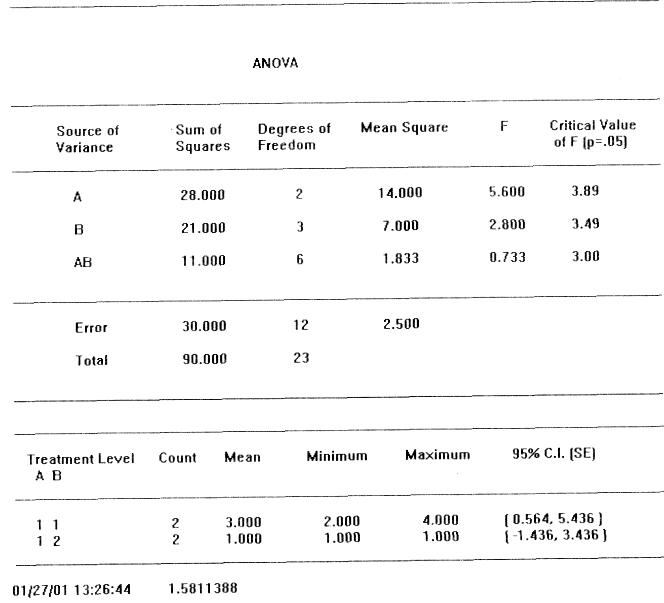Puc.

9.3 Для увеличения степени свободы остаточного члена можно ис­пользовать два подхода. Первый просто увеличивает число повторе­ний в эксперименте. Этот подход обычно более дорогой, но может быть весьма эффективным. Второй касается плана эксперимента и статистической модели дисперсионного анализа.

Средний квадрат ошибки – фактически остаточный член, оставшийся после удаления других квадратов. Если можно найти приемлемый способ, который позволит большему количеству данных оставаться после удаления эффектов, то получим оценку стандартной ошибки c большим числом степеней свободы. Окончательное значение F-критерия будет умень­шаться при увеличении мощности анализа.

При этом фактически иг­норируются некоторые из взаимодействий. В многофакторных экспериментах для упрощения статистиче­ской модели и уменьшения количества экспериментов игнорируют взаимодействия самого высокого порядка.

Например, статистическая модель c двумя факторами без учета их взаимодействия имеет сле­дующий вид: 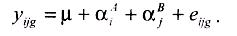Если действительно эффектами этих взаимодействий можно пренебречь, то это позволит использовать дополнительные степени свободы для получения лучших оценки F-статистики. Кроме того, большее число степеней свободы означает также и меньшее значение F-критерия.

Однако необходимо понимать, что удаление членов из статистической модели предполагает, что не существует взаимодей­ствий более высоких порядков. В GPSS World от учета взаимодействий высоких порядков мож­но отказаться, используя третий параметр процедуры ANOVA. Ино­гда целесообразней учитывать только одну случайность.

В этом случае для улучшения статистических оценок просто добавляются по­вторения наблюдений. Число повторений задается во втором пара­метре процедуры ANOVA. Для работы процедуры ANOVA ей необходимо передать имя GPSS-матрицы c сохраненными результатами всех прогонов модели. Можно иметь несколько матриц результатов и для каждой их них вы­полнить эту процедуру.

Любые матрицы GPSS World могут иметь максимальную размерность 6, эта величина ограничивает максималь­ное число анализируемых факторов. Прежде чем начать эксперимент, необходимо инициализировать элементы матрицы в НЕОПРЕДЕЛЕННОЕ (UNSPECIFIED) состоя­ние c помощью оператора: INITIAL MyResuItMatrix,UNSPECIFIED Этот оператор сообщает программе ANOVA, что эксперимент не был закончен.

Позиция в матрице результатов для каждого результата экспе­римента определена комбинацией уровней обработки, как было пока­зано в таблице 9.1. Например, если в эксперименте рассматривается 3 вида рабочих и два значения их численности (минимальное и макси­мальное) для каждого вида, то результат моделирования для третьего вида c максимальной численностью помещается в матрицу результа­тов в позицию [3, 2].

Так как число повторений указывается в третьем индексе матрицы, то результат первого прогона этой комбинации уровней обработки помещается в элемент [3, 2, 1] матрицы результа­тов. Каждое измерение в матрице результатов анализируется библио­течной процедурой ANOVA, как фактор.

Размерность матрицы ре­зультатов должна быть, по крайней мере, такой же, как и число уров­ней обработок этого фактора или максимальное рассчитанное число повторений. Нет никакого предела для числа уровней обработок фак­торов (вернее, предел накладывается только виртуальной памятью используемого компьютера).

Пример 9.2 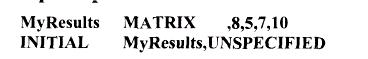В этом примере созданная матрица результатов может содержать результаты эксперимента c 4-мя факторами (по числу заданных опе­рандов – В, C, D, E) или c З-мя факторами (операнды В, C, D) и 10-ю повторениями прогонов (последний операнд). Фактор А может иметь до 8-х уровней обработок, фактор В может иметь до 5 и так далее.

Оператор INITIAL устанавливает все элементы в матрице в со­стояние UNSPECIFIED. При обращении к процедуре ANOVA надо задать 3 параметра. Первый – имя матрицы результатов, например, MyResults. Второй необязательный параметр – размерность (индекс) мат­рицы результатов, которую нужно использовать для повторений.

Каждый уровень в этой размерности представляет прогон c различными начальными значениями случайных чисел. Процедура ANOVA ис­пользует информацию, связанную c числом повторений прогонов для оценки стандартной ошибки. Чем больше повторений, тем больше число степеней свободы и тем точнее статистические результаты мо­делирования.

Некоторые экспериментальные планы не используют размер­ность повторения. В том случае второй параметр равен 0. Третий параметр задает взаимодействия между факторами, ко­торые будут включены в статистическую модель. Если параметр ра­вен 2, то взаимодействия второго порядка будут включены в анализ. Если параметр равен 1, то взаимодействия не будут учитываться.

При равенстве значения параметра 3 – взаимодействия 2-го и 3-го поряд­ков будут включены в статистическую модель. Взаимодействия более высоких порядков GPSS World не поддерживает. Еще раз отметим, что если при экспериментировании c моделью не учитываются взаи­модействия между факторами, то это увеличивает число степеней свободы и улучшает оценки стандартной ошибки. Главная цель процедуры ANOVA состоит в создании стандарт­ной таблицы ANOVA, где указывается окончательная F-статистика и ее критическое значение. Кроме того, при вызове процедуры ANOVA из программы PLUS при завершении процедуры возвращается стан­дартная ошибка.

Источник: studfile.net