Чалыкина, Е. Г. Разработка и конструирование логического калькулятора / Е. Г. Чалыкина, И. В. Сухан. — Текст : непосредственный // Молодой ученый. — 2018. — № 20 (206). — С. 39-44. — URL: https://moluch.ru/archive/206/50486/ (дата обращения: 17.06.2023).
В статье описан процесс разработки и создания собственного логического калькулятора, позволяющего решать основные расчетные задачи математической логики.
В сети Интернет имеется большое количество пользовательских программ, доступных для online-использования или для скачивания. В том числе есть и программы-«попытки» анализа логических формул, но ни одна не содержит всех необходимых компонентов анализа, либо вовсе предоставляет некорректный результат. В ходе анализа соответствующего потребительского рынка были выявлены основные проблемы, встречающиеся во всех инструментах для работы с логическими формулами: недостаток основных компонентов для анализа формулы; неграмотное использование алгоритмов, что приводит в большинстве случаев к некорректному результату; неудобный пользовательский интерфейс. Зачастую с попыткой компенсации последнего недостатка определяется еще одна основная проблема — неинформативно составленная инструкция к пользованию программой, или же, напротив, нагромождение таковой излишней информацией.
Программируемые графические калькуляторы! Casio fx-cg50
Был разработан логический калькулятор со следующими возможностями обработки логической формулы: построение таблицы истинности; определение типа формулы; определение класса формулы; определение логического следования; нахождение конъюнктивной и дизъюнктивной нормальных форм и соответствующих совершенных форм; построение упрощенной формы; построение полинома Жегалкина.
Из анализа пользовательских потребностей следует, что программа должна соответствовать следующим требованиям: удобный интерфейс; возможность применения стандартных функций ОС Windows: копирования и вставки; возможность ввода информации с клавиатуры; возможность корректирования введенной формулы; обработка ошибок ввода с выводом соответствующего сообщения.
Основой для содержательного и комплексного ответа на заявленные требования является качественно продуманный интерфейс калькулятора.
Код программы организован посредством нескольких связанных между собой классов. Каждый класс отвечает за определенную функцию в программе. Базовым для всех операций является класс для построения таблицы истинности. Таблица истинности необходима для поиска корректного ответа при запросе любой опции, заявленной в калькуляторе, поэтому программно реализованный класс таблицы истинности используется во всех других классах, то есть является родителем.
При запуске программы открываются два окна: стартовая страница (рисунок 1) и главное окно программы (рисунок 2).
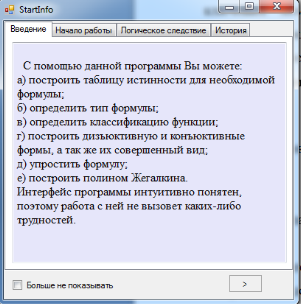
Рис. 1. Стартовая страница программы
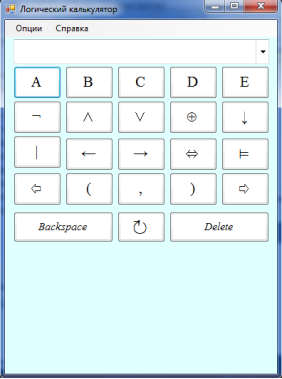
Рис. 2. Главное окно программы
Пользователю предлагается ввести формулу, содержащую до пяти переменных, однако есть возможность использования ввода с клавиатуры, что значительно увеличивает максимальное количество используемых переменных. Программа может обрабатывать девять заявленных операций (инверсия, конъюнкция, дизъюнкция, сложение по модулю два, стрелка Пирса, Штрих Шеффера, импликация, репликация, эквивалентность), причем их приоритетность соответствует порядку следования операций в формате чтения (слева направо).
Информатика ОГЭ 2020 — задание 5. Анализ алгоритмов для исполнителя (калькулятор)
По завершении программной реализации каждая опция калькулятора была протестирована на индивидуально подготовленной выборке, которая учитывала все возможные конфликтные ситуации. При обнаружении сбоев были внесены необходимые корректировки, после чего производилось повторное тестирование. После чего был сделан вывод, что программа пригодна для анализа любой логической формулы, все опции калькулятора работают исправно.
Приведем несколько примеров.
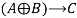
Для тестирования опции «Класс» пример был подобран таким образом, чтобы программа определила отношение формулы к классу «Сохраняющая константу» сразу в двух случаях. В соответствии с правилом классификации, формула является сохраняющей константы 1 и 0 одновременно (рисунок 3).
Рис. 3. Демонстрация опции «Класс»
Программа верно отрабатывает конфликтную ситуацию и производит корректную классификацию формулы.
Определение типа формулы представлено на рисунке 4.
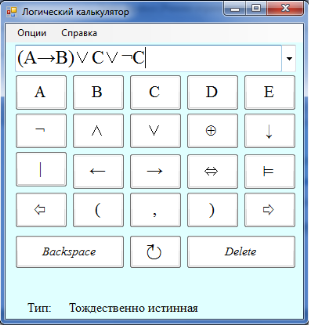
Рис. 4. Демонстрация опции «Тип» на примере тождественно истинной формулы
Проверка логического следования представлена на рисунке 5.
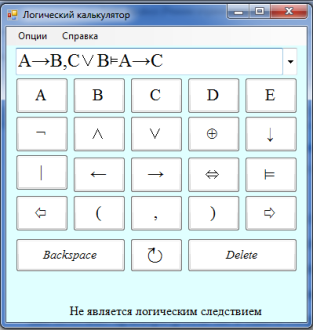
Рис. 5. Демонстрация опции «Логическое следствие»
Тестирование опции «СКНФ и СДНФ» было принято осуществить на трех примерах: СКНФ отсутствует, СДНФ отсутствует и есть обе совершенные формы. Программа всегда выдает верный результат (рисунки 6, 7).
.
Рис. 6. Вывод результата для тождественно истинной формулы
.
Рис. 7. Вывод результата для опции «СКНФ и СДНФ»
Опция «Упрощенный вид» является самой сложной в реализации по отношению к другим. Это обусловливается большим количеством содержащихся в ней вычислительных операций. Необходимо отметить, что для некоторых формул существует два или более варианта упрощенного вида (минимальной ДНФ). Формулой для теста стала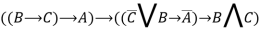 
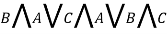и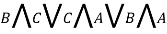 
. Результат работы программы приведен на рисунке 8.
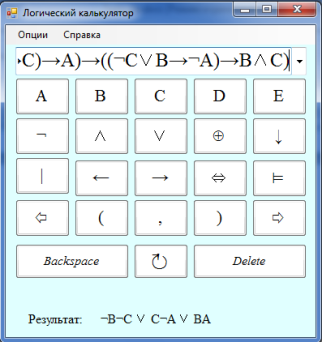
Рис. 8. Демонстрация опции «Упрощенный вид»
Из иллюстрации видно, что программа вывела один из заявленных результатов, при нахождении удовлетворяющего результата работа программы была корректно завершена.
Программа обладает функцией сохранения истории. Сохранение истории предполагает необходимость ее очистки, следовательно, была создана кнопка очистки истории.
Созданная программа выгодно выделяется на фоне подобных разработок. Во-первых, функциональность калькулятора значительно выше, чем у других. Во-вторых, интерфейс и его составляющие в первую очередь адаптированы под пользователя, которым может быть как студент в целях обучения, так и преподаватель — для более быстрого и эффективного анализа проверочных работ обучающихся.
Основные термины (генерируются автоматически): демонстрация опции, программа, вывод результата, главное окно программы, истинная формула, логическая формула, логическое следование, некорректный результат, опция калькулятора, построение таблицы истинности.
Похожие статьи
Решение логической задачи разными способами и сравнение их.
Ключевые слова: логика, логическая задача, алгебра логики, метод таблиц, метод рассуждений.
Оба выше приведенных способа дают результат при решении данной задачи.
Iспособ. С использованием таблицы истинности.
Построение логических схем с использованием Matlab/Simulink.
Рис. 2. Программа «Анализ и синтез логических систем управления» [1].
Область построения логической схемы разобьем на 4 блока: блок входных переменных, блок инверсий (может отсутствовать), блок логических операций и блок результата (рис. 5). В.
Применение булевых функций к релейно-контактным схемам
Из этого можно сделать вывод, что методы логического анализа и синтеза
Построение логических схем с использованием Matlab/Simulink.
Схемы и таблицы на уроках истории помогают выделить главное, они «запирают» информацию в замкнутое пространство.
Особенности изучения способа тестирования базового пути.
Цикломатическая сложность — это метрика программного обеспечения, которая обеспечивает количественную оценку логической сложности программы.
— количество узлов потокового графа ; 3) Цикломатическая сложность формируется по формуле
Равносильные преобразования формул. Нормальные формы. СДНФ. СКНФ. Логическое следование.
Модуль 3. Исчисление высказываний. Аксиоматическое построение логики высказываний. Аксиомы, правила вывода.
Создание и использование программы для статистического.
Цена игры находится по формуле: , а вероятности использования тактик игроком 2 по формуле: . Из таблицы, в которой содержатся значения
Интерфейс и пример решения показан на рис. 1. Рис. 1. Демонстрация интерфейса и решения с помощью прикладной программы.
Формирование логического мышления учащихся через.
Анализ основной образовательной программы по математике [5] показывает, что развитие мышления учащихся (в том числе, логического
Осталось подставить найденные значения х в формулу 3х‑2у‑12=0. Если х=2, то у=‑3. Если х= , то у=‑5. Ответ: (2; ‑3), ( ; ‑6) (рис. 4).
Метод обобщённого правила рекурсии как средство развития.
Одно из основных преимуществ языка Пролог — возможность создания программы в терминах решаемой задачи.
Этот метод позволяет решить практически любую задачу в Прологе путём построения правильных логических формул на языке предикатов.
Использование прогнозной аналитики.
Результатом такого обучения будет сформированная программой модель, которая
Успех построения прогнозной модели зависит, прежде всего, от объема истории и ширины профиля
Исходя из данных таблицы формируется вывод, что используемый метод прогнозирования.
Источник: moluch.ru
На примере «Калькулятора»
Тесты, проделанные нами на прошлом семинаре, как правило, проводятся не вручную. Для целей тестирования пишут специальную программу — тестовый драйвер, который и проводит тестирование. Более того, такие программы часто пишутся на другом языке, нежели тестируемая программа, или создаются автоматически, с помощью специальных утилит.
Синицын С.В., Налютин Н.Ю. Верификация программного обеспечения
На этом семинаре мы сами напишем простой тестовый драйвер на C# для тестирования функций «Калькулятора», используя спецификацию второго семинара.
Замечание. Код программы слегка изменен для упрощения компиляции отдельных модулей. Так, исключена работа с переменной
Program.res,а класс CalcClass объявлен как public.
Для начала рассмотрим функцию деления. Тест-требования к ней мы уже составили. Для простоты будем пользоваться лишь четырьмя общими тест- требованиями.
- 1. Оба входных параметра принадлежат допустимой области, и выходное значение принадлежит допустимой области.
- 2. Первый входной параметр принадлежит допустимой области, второй не принадлежит допустимой области
- 3. Первый входной параметр не принадлежит допустимой области, второй принадлежит допустимой области
- 4. Оба входных параметров принадлежат допустимой области, а значение функции не принадлежит допустимой области.
private void buttonStartDel_Click(object sender, EventArgs e)
richTextBoxl.Text = richTextBoxl.Text += ‘Test Case l «;
richTextBoxl.Text += ‘Входные данные: a= 78508, b = -304 «; richTextBoxl.Text += «Ожидаемый результат: res = 78204 error = ‘»»+’ «;
int res = CalcClass.Add(78508, -304); string error = CalcClass.lastError; richTextBoxl.Text += ‘Код ошибки:» + error + » «; richTextBoxl.Text += ‘Получившийся результат: » +»res = «+ res.ToString() +» error = ‘Terror. ToString() +» «; if (res == 78204 error == «»)
Синицын С.В., Налютин Н.Ю. Верификация программного обеспечения
richTextBoxl.Text += ‘Тест пройденпп»;
richTextBoxl.Text += ‘Тест не пройденпп»;
catch (Exception ex)
richTextBoxl.Text += «Перехвачено исключение: » + ex.ToString() + «пТест не пройденЛп»;
richTextBoxl.Text += ‘Test Case 2 «;
richTextBoxl.Text += ‘Входные данные: a= -2850800078, b = 3000000000 «;
richTextBoxl.Text += «Ожидаемый результат: res = 0 error = YError 06» «;
int res = CalcClass.Add(-2850800078, 3000000000); string error = CalcClass.lastError; richTextBoxl.Text += «Код ошибки:» + error + » «; richTextBoxl.Text += ‘Получившийся результат: » + «res = » + res.ToString() + » error = » + error.ToString() + » «; if (res == 0 error == ‘Error 06»)
richTextBoxl.Text += ‘Тест пройденпп»;
richTextBoxl.Text += ‘Тест не пройденпп»;
catch (Exception ex)
richTextBoxl.Text += ‘Перехвачено исключение: » + ex.ToString() + «пТест не пройденЛп»;
richTextBoxl.Text += ‘Test Case 3 «;
richTextBoxl.Text += ‘Входные данные: a= 3000000000, b = — 2850800078 «;
richTextBoxl.Text += «Ожидаемый результат: res = 0 error = «Error 06» «;
int res = CalcClass.Add(3000000000, -2850800078); string error = CalcClass.lastError; richTextBoxl.Text += «Код ошибки: » + error+» «; richTextBoxl.Text += «Получившийся результат: » + «res = » + res.ToStringO + » error = » + error.ToString() + » «; if (res == 0 error == ‘Error 06»)
richTextBoxl.Text += ‘Тест пройденпп»;
richTextBoxl.Text += ‘Тест не пройденпп»;
catch (Exception ex)
richTextBoxl.Text += ‘Перехвачено исключение: » + ex.ToString() + «пТест не пройденЛп»;
richTextBoxl.Text += ‘Test Case 4 «;
richTextBoxl.Text += ‘Входные данные: a= 2000000000, b = 2000000000 «;
richTextBoxl.Text += «Ожидаемый результат: res = 0 error = YError 06» «;
int res = CalcClass.Add(2000000000, 2000000000); string error = CalcClass.lastError; richTextBoxl.Text += ‘Код ошибки: » + error +» «; richTextBoxl.Text += ‘Получившийся результат: » + «res error = » + error.ToString() + » «; if (res == 0 error == ‘Error 06»)
richTextBoxl.Text += ‘Тест пройденпп»;
richTextBoxl.Text += ‘Тест не пройденпп»;
catch (Exception ex)
richTextBoxl.Text += «Перехвачено исключение: » + ex.ToString() + «пТест не пройденЛп»;
Листинг 7.1. Текст программы
Каждый тестовый пример находится внутри блока try-catch для того, чтобы перехватить любое сгенерированное исключение внутри методов Add () .
При этом файл CalcClass.dll, в котором и реализованы все математические методы, необходимо добавить в References проекта.
Проведем тестирование и получим следующий результат:
Входные данные: а= 78508, b = -304 Ожидаемый результат: res = 78204 error = «»
Получившийся результат: res = 78204 error =
Входные данные: а= -2850800078, b = 3000000000 Ожидаемый результат: res = 0 error = ‘Error 06″
Код ошибки: Error 06
Получившийся результат: res = 0 error = Error 06
Синицын С.В., Налютин Н.Ю.
Тест пройден Test Case 3
Входные данные: а= 3000000000, b = -2850800078 Ожидаемый результат: res = 0 error = ‘Error 06″
Код ошибки: Error 06
Получившийся результат: res = 0 error = Error 06 Тест пройден
Входные данные: а= 2000000000, b = 2000000000 Ожидаемый результат: res = 0 error = ‘Error 06″
Код ошибки: Error 06
Получившийся результат: res = 0 error = Error 06 Тест пройден
Точно такой же результат мы бы получили и при ручном тестировании, если бы выявленные ошибки были исправлены. Заметим, что при таком подходе к тестированию нам удается локализовать ошибки. Если что-то работает не так, как надо, то можно с уверенностью утверждать, что ошибка содержится именно в функции деления, в то время, как на прошлом семинаре мы не могли сказать, где именно она произошла.
Замечание. Мы считаем, что тестовый драйвер сам не содержит ошибок. Тестирование тестового драйвера выходит за пределы изучаемой темы.
7.4.1. Программа
Будут выданы .dll файлы, которые нужно протестировать методом «черного ящика», и пример тестового драйвера.
Составить тест-план и провести модульное тестирование следующих методов:
1. Нахождение остатка.
/// Деление по модулю ///
/// ocTaTOK public static int Mod(long a, long b)
Ш унарный плюс ///
III public static int ABS(long a)
3. Унарный минус.
Ш унарный минус ///
III public static int IABS(long a)
Ш вычитание III
уменыпаемое Ш
вычитаемое III pa3HOCTb public static int Sub(long a, long b)
Синицын С.В., Налютин Н.Ю.
множитель /// npoH3BefleHHe public static int Mult(long a, long b)
Ш частное III
III 4acTHoe public static int Div(long a, long b)
Источник: bstudy.net
Проект по информатике «Разработка калькулятора для решения квадратного уравнения в среде программирования Pascal»
Моя цель работы: Разработать калькулятор для решения квадратного уравнения в среде программирования Pascal .
Моя гипотеза: подростки могут разработать калькулятор для решения любого квадратного уравнения.
Объект исследования: разработка калькулятора .
Предмет исследования: программирование.
Практическая значимость: данный материал может быть использован для самообучения, на дополнительных уроках информатики.
Скачать:
Предварительный просмотр:
МАОУ «Средняя общеобразовательная школа № 24 с углубленным изучением отдельных предметов»
«Разработка калькулятора для решения квадратного уравнения в среде программирования Pascal»
Ученика 9 «Д» класса
1.1. Способы решения квадратного уравнения
1.2. Изучение языка программирования Paskal
2.1. Проектирование прототипа калькулятора
2.2. Моделирования прототипа с использованием языка программирования.
2.3. Тестирование и откладка программного продукта.
3. Список литератур
Моя цель работы: Разработать калькулятор для решения квадратного уравнения в среде программирования Pascal.
Моя гипотеза: подростки могут разработать калькулятор для решения любого квадратного уравнения.
Объект исследования: разработка калькулятора .
Предмет исследования: программирование.
Практическая значимость: данный материал может быть использован для самообучения, на дополнительных уроках информатики.
Актуальность темы: Для программиста создать программу калькулятор, является начальным этапом по созданию сложным программ.
1.1.Способы решения квадратных уравнений
Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ : Разложение левой части уравнения на множители.
х 2 + 10х — 24 = 0.
Разложим левую часть на множители:
х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х 2 + 6х — 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2* х * 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2* х * 3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
прибавляя к ней и вычитая 3 2 . Имеем:
х 2 + 6х — 7 = х 2 + 2* х * 3 + 3 2 — 3 2 — 7 = (х + 3) 2 — 9 — 7 = (х + 3) 2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 — 16 =0, (х + 3) 2 = 16.
Следовательно, х + 3 — 4 = 0, х 1 = 1, или х + 3 = -4, х 2 = -7.
3. СПОСОБ : Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах 2 + bх + с = 0, а ? 0
на 4а и последовательно имеем:
4а 2 х 2 + 4аbх + 4ас = 0,
((2ах) 2 + 2ах * b + b 2 ) — b 2 + 4ac = 0,
(2ax + b) 2 = b 2 — 4ac,
2ax + b = ± v b 2 — 4ac,
2ax = — b ± v b 2 — 4ac,
а) Решим уравнение: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 — 4ac = 7 2 — 4 * 4 * 3 = 49 — 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b 2 — 4ac >0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х 2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b 2 — 4ac = (-4) 2 — 4 * 4 * 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах 2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 — 4ac = 3 2 — 4 * 2 * 4 = 9 — 32 = — 13 , D
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b 2 — 4ac
уравнение ах 2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р
x 2 — 3x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = — 3
x 2 + 8x + 7 = 0; x 1 = — 7 и x 2 = — 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q 0 .
x 2 + 4x — 5 = 0; x 1 = — 5 и x 2 = 1, так как q= — 5 0;
x 2 — 8x — 9 = 0; x 1 = 9 и x 2 = — 1, так как q = — 9
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + bх + с = 0, где а ? 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.
х 1 = у 1 /а и х 1 = у 2 /а.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х 2 — 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 — 11у + 30 = 0.
Согласно теореме Виета
у 1 = 5 х 1 = 5/2 x 1 = 2,5
у 2 = 6 x 2 = 6/2 x 2 = 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение
ах 2 + bх + с = 0, где а ? 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1,
Доказательство. Разделим обе части уравнения на а ? 0, получим приведенное квадратное уравнение
x 2 + b/a * x + c/a = 0.
Согласно теореме Виета
По условию а — b + с = 0, откуда b = а + с. Таким образом,
x 1 + x 2 = — а + b/a= -1 — c/a,
x 1 x 2 = — 1* ( — c/a),
т.е. х 1 = -1 и х 2 = c/a, что м требовалось доказать.
1) Решим уравнение 345х 2 — 137х — 208 = 0.
Решение. Так как а + b + с = 0 (345 — 137 — 208 = 0), то
х 1 = 1, х 2 = c/a = -208/345.
2)Решим уравнение 132х 2 — 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 — 247 + 115 = 0), то
х 1 = 1, х 2 = c/a = 115/132.
- Изучение языка программирования Paskal.
Язык был создан Никлаусом Виртом в 1968—1969 годах после его участия в работе комитета разработки стандарта языка Алгол-68 . Язык назван в честь французского математика, физика, литератора и философа Блеза Паскаля , который создал одну из первых в мире механических машин, складывающую два числа . Первая публикация Вирта о языке датирована 1970 годом; представляя язык, автор в качестве цели его создания указывал построение небольшого и эффективного языка, способствующего хорошему стилю программирования, использующему структурное программирование и структурированные данные.
Особенностями языка являются строгая типизация и наличие средств структурного (процедурного) программирования . Паскаль был одним из первых таких языков. По мнению Вирта, язык должен способствовать дисциплинированному программированию, поэтому, наряду со строгой типизацией, в Паскале сведены к минимуму возможные синтаксические неоднозначности, а сам синтаксис автор постарался сделать интуитивно понятным даже при первом знакомстве с языком.
2.1. Проектирование прототипа калькулятора.
Для создания прототипа калькулятора, мне понадобится среда программирования pascal. Для прототипа я использовал программу PascalABC.
1.Для начала обозначим все необходимые значения действительными числами, используя команду :real
2. Далее обозначаем начало нашего калькулятора, с помощью команды writeln и readln.
3.Вводим формулу дискриминанта и обозначаем, что для всех значений D
4.расписать действия для всех возможных исходив:
1.если дискриминант равен 0.
2.если дискриминант положительный .
X2:=(-b-sqrt(d))/2/a
Исходя из этих действий мой прототип имеет следующий вид:
if d then writeln(‘кореней нет’);
2.2 Моделирование прототипа с использование языка программирования.
Прототип — это моделирование конечного продукта. Это интерактивный макет, который может иметь любую степень точности. Основная цель создания прототипов – проверить, насколько последователен путь пользователя, и выявить препятствия, которые могут возникнуть в процессе его взаимодействия с продуктом.
Прототипы не только позволяют проверить юзабилити разрабатываемого продукта до начала написания кода, они также приводят к неожиданным открытиям и новым идеям, которые могут вывести проектируемый продукт на новый уровень (а могут и нет).
2.3. Тестирование и откладка программного продукта.
Тестирование программного средства (ПС) — это процесс выполнения программ на некотором наборе данных, для которого заранее известен результат применения или известны правила поведения этих программ. Указанный набор данных называется тестовым или просто тестом . Тестирование программ является одной из составных частей более общего понятия — «отладка программ». Под отладкой понимается процесс, позволяющий получить программу, функционирующую с требующимися характеристиками в заданной области изменения входных данных.
Во время тестирования и откладки программного продукта я не выявил критических ошибок. И считаю, что мой продукт готов к использованию.
1. ТЕХНОЛОГИЯ РАЗРАБОТКИ ПРИКЛАДНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Соловьев С. В., Цой Р. И., Гринкруг Л. С
- Википедия.
- Сайт infoshell.
Поделиться:
Нас с братом в деревню отправили к деду.
«Портрет». Н.В. Гоголь
Зимняя ночь. Как нарисовать зимний пейзаж гуашью
Как представляли себе будущее в далеком 1960-м году
Агния Барто. Сережа учит уроки
Источник: nsportal.ru