Алгоритмы и программы как информационные модели

6.1.1. Различные подходы к понятию “алгоритм”. Алгоритм – одно из фундамен — тальных понятий информатики . Алгоритмизация наряду с моделированием выступает в ка — честве общего метода информатики . Особенность положения состоит в том , что при реше — нии практических задач , предполагающих разработку алгоритмов для реализации на ЭВМ , почти всегда можно не опираться на высокую формализацию данного понятия . В таких слу — чаях достаточно содержательного толкования понятия алгоритма и рассмотрения его основ — ных свойств . При таком подходе алгоритмизация выступает как набор определенных прак — тических приемов , особых навыков рационального мышления в рамках заданных языковых средств . Понятие алгоритма в математике прошло большой путь развития . Общее определение алгоритма , имеющее интуитивный характер следующее . Алгоритм – это общий , единообразный , точно установленный способ решения любой задачи из данной массовой проблемы . Таким образом , алгоритм всегда связан с решением массовой проблемы . Задачи такого класса отличаются друг от друга значениями входящих в них параметров . Примеры алгоритмов : извлечение квадратного корня , предельный переход , нахождение производной и тому подобное . Приведенное понятие алгоритма нестрогое . В нем встречаются слова , точный смысл которых не установлен , например , “ способ ”. Тем не менее , даже при таком определении можно выделить некоторые характерные черты алго — ритма : § дискретность . Каждая последующая величина получается из значений преды — дущих по определенному закону . Все величины получаются последовательно друг за другом ; § детерминированность . Между всеми величинами , получаемыми алгоритмом , существует жесткая причинная связь . Последующие значения зависят от пре — дыдущих ; § элементарность шагов алгоритма . Закон получения последующей системы ве — личин из предшествующей должен быть простым ; § массовость . Начальная система величин выбирается из некоторого множества . Начальные условия могут варьироваться в бесконечных пределах ; § результативность . Конечный результат всегда должен быть получен . Описанные свойства алгоритма следует считать эмпирическими . Они выявлены на основе обобщения свойств алгоритмов различной природы и имеют прикладной характер . Слово “ алгоритм ” происходит от имени математика аль Хорезми ( ал Горезми – алгоритм ). Интуитивное понятие алгоритма работает , когда речь идет о найденном алгоритме решения конкретной задачи . Положение существенно меняется , если возникает алгоритмическая про — блема , решение которой не найдено , и требуется установить , имеет ли она решение . В этом случае надо доказать либо существование алгоритма , либо его отсутствие . Первое можно сделать путем фактического описания процесса , решающего задачу . В этом случае достаточ — но и интуитивного понятия алгоритма , чтобы удостовериться в том , что описанный процесс есть алгоритм . Доказать не существование алгоритма таким путем невозможно . Для этого необходимо точное формальное определение . В уточнении понятия алгоритма выделяются три направления : Абу Джафар Мухаммад ибн Муса ал — Хорезми ( ок . 783- ок . 850) – арабский математик .

АЛГОРИТМЫ в ПРОГРАММИРОВАНИИ для новичков | Левенштейн, Фибоначчи, Факториал и т.д.

q уточнение понятия эффективно вычислимой функции . Этим занимались А . Чёрч и К . Гёдель . В результате был выделен класс частично рекурсивных функций , имеющих строгое математическое определение ; q машинную арифметику . Здесь сущность понятия алгоритма раскрывается пу — тем рассмотрения процессов , осуществляемых в вычислительной машине ; q направление , связанное с понятием нормальных алгоритмов из работ А . Маркова . Существование различных определений понятия алгоритма имеет и свои преимуще — ства , так как для решения различных задач удобно использовать различные наиболее подхо — дящие для этого случая определения . Первое направление уточнение – понятия алгоритма – связано с точным описанием специального класса функций , называемых рекурсивными . Числовые функции , значения ко — торых можно вычислить посредством алгоритма , называются вычислимыми функциями . По — нятие алгоритма здесь не определено формально точно , поэтому понятие вычислимой функ — ции оказывается интуитивным . Однако совокупность вычислимых функций , соответствую — щих условиям 1-5, т . е . удовлетворяющих характерным чертам алгоритма для многих процес — сов , оказалась одной и той же , легко описываемой в математических терминах . Эта точно описанная совокупность числовых функций , совпадающая с совокупностью всех вычисли — мых функций при самом широком понимании алгоритма , называется совокупностью рекур — сивных функций . Рекурсивные функции впервые описаны Гёделем , затем в 1936 году Чёрч пришел к такому же классу функций . Анализ идей , лежащих в основе определения рекурсивных функ — ций , позволил Чёрчу высказать гипотезу о том , что класс рекурсивных функций тождестве — нен с классом всюду определенных вычислимых функций . Эта гипотеза известна под именем тезиса Чёрча ; доказать ее нельзя , так как понятие вычислимой функции точно не определе — но . В силу тезиса Черча вопрос о вычислимости функции равносилен вопросу о её рекурсив — ности . Понятие рекурсивной функции строгое . Поскольку в алгоритмических проблемах речь обычно идет не об алгоритмах , а о вычислимости некоторых , специальным образом по — добранных решающих проблему функциях , то можно строго доказать , что решающая кон — кретную задачу функция не может быть рекурсивной , а , следовательно , не существует и ал — горитма решения этой задачи . Именно этим путем Чёрч доказал неразрешимость алгоритми — ческой проблемы логики предикатов . Если первое направление уточняет понятие алгоритма через класс рекурсивных функ — ций , то второе , связанное с машинной арифметикой , сначала уточняет понятие алгоритма , а затем определяет класс вычислимых функций . Это направление развито Э . Постом и А . Тьюрингом . Основная идея этого направления заключается в том , что алгоритмиче — ские процессы – это процессы , которые могут имитироваться на подходяще построенных машинах , которые описываются в точных математических терминах . В результате оказыва — ется , что сложные процессы можно моделировать на простых устройствах . Всякий алгоритм может быть задан некоторой функциональной схемой и реализован в соответствующей ма — шине Тьюринга . Эта гипотеза называется тезисом Тьюринга . Его также нельзя доказать , по той же причине , что и тезис Чёрча . Все известные до сих пор алгоритмы могут быть заданы посредством тьюринговых функциональных схем . Третье направление – теория нормальных алгоритмов Маркова . Алонзо Чёрч (1903 – 1995) – американский математик и логик . Курт Фридрих Гёдель (1906 – 1978) – немецкий математик и логик . Андрей Андреевич Марков (1903 – 1979) – советский математик . Эмиль Леон Пост (1897 – 1954) – американский математик и логик . Алан Матисон Тьюринг (1912 – 1954) – английский математик .

Будем называть алфавитом A всякое непустое конечное множество символов , сами символы называются буквами . Словом в алфавите A называется всякая конечная последова — тельность букв этого алфавита . Простейшими действиями в нормальных алгоритмах Марко — ва являются последовательные замены вхождений подслов специального вида на другие сло — ва . Нормальный алгоритм может переводить слово α в слово β , причем на множестве слов используемого алфавита слово β однозначно определяется этим алфавитом и словом α . Нормальный алгоритм может быть и не применим к слову α , если он не преобразует α ни в какое слово . Основное положение об “ универсальности ” нормальных алгоритмов – принцип нор — мализации : любой алгоритм над конечным алфавитом A эквивалентен относительно A не — которому нормальному алгоритму над A . Этот принцип подобен тезисам Чёрча и Тьюринга и недоказуем из — за неопределенности формального понятия алгоритма . На практике доста — точно ограничиться алгоритмами , действующими на последовательностях натуральных чи — сел и выдающих в качестве значений также последовательности натуральных чисел . Дейст — вия нормальных алгоритмов Маркова похожи на действия машин Тьюринга . Все эти возникшие исторически независимо друг от друга подходы оказались впо — следствии эквивалентными . Вместе с тем , формально определенный любым из известных способов алгоритм не может в практическом программировании заменить данное в начале текущего раздела нестрогое определение . Основная причина состоит в том , что формальное определение резко сужает круг рассматриваемых задач , делая многие практически важные задачи недоступными для рассмотрения .

6.1.2. Графическое представление алгоритмов . Алгоритм , составленный для неко —

торого исполнителя , можно представить различными способами : с помощью графического или словесного описания , в виде таблицы , последовательностью формул , записанным на ал — горитмическом языке . Рассмотрим следующие способы описания алгоритма : словесное опи — сание , псевдокод , блок — схема , программа . Словесное описание представляет структуру алгоритма на естественном языке . Ника — ких правил составления словесного описания не существует . Этот способ строго не форма — лизуем , допускает неоднозначность толкования при описании некоторых действий , страдает многословностью , поэтому не имеет широкого распространения . Псевдокод – описание структуры алгоритма на естественном , но частично формали — зованном языке . В псевдокоде используются некоторые формальные конструкции и обще — принятая математическая символика , и он позволяет выявить основные этапы решения зада — чи перед точной ее записью на языке программирования . Единого формального определения псевдокода не существует , поэтому возможны различные псевдокоды . Блок — схема – это описание структуры алгоритма с помощью геометрических фигур с линиями — связями , показывающими порядок выполнения отдельных инструкций , т . е . это ориентированный граф , указывающий порядок исполнения команд алгоритма . Этот способ весьма нагляден , обеспечивает “ читаемость ” алгоритма . Описания алгоритма в словесной форме , на псевдокоде или в виде блок — схемы допускает некоторый произвол при изображении команд . Вместе с тем эти способы позволяют человеку понять суть дела и исполнить алгоритм . Однако для компьютера алгоритм должен быть записан на “ понятном ” ему языке , такой формализованный язык называют языком программирования . Программа – описание структуры алгоритма на языке программирования .

Рассмотрим подробнее некоторые конструкции , использующиеся для построения
блок — схем ( см . рис . 6.1 а — д ). Блоки , характеризую —
		щие начало и конец алгоритма , изображаются
а	Начало			Конец
			прямоугольником со скругленными вершинами ;
обычным прямоугольником – блоки , предназна —
		ченные для описания отдельных действий . Анало —
гичным образом изображаются блоки для вво —
		б	Действие		Ввод / Вывод		в		да / вывода с неопределенного носителя и вывода
на печатающее устройство . Наконец , условный
		блок изображается в виде ромба . Вершины графа ,
представляющего блок — схему , могут быть одного
		из трех типов : функциональная вершина	( F ) ,
г	Вывод на			Нет	Проверка		Да	д имеющая один вход и один выход , предикатная
печать		условия		вершина ( P ) , имеющая один вход и два выхода , в
этом случае функция P передает управление по
		Рис . 6.1. Основные конструкции блок — схем								одной из ветвей в зависимости от значения	P ,
объединяющая вершина ( U ) , обеспечивающая пе —

редачу управления от одного из двух входов к выходу . Особое значение для практики алго — ритмизации имеют четыре блок — схемы : композиция или следование ( рис . 6.2 а ); альтернати — ва или ветвление ( рис . 6.2 б ); итерация или цикл с предусловием ( рис . 6.2 в ) или постуслови — ем ( рис . 6.2 г ).

U	U
нет			да		да
						F1	P	P	F
F1			F2							нет	да
F2
	U	F	P
нет
		а	б	в		г

Рис . 6.2. Основные алгоритмические структуры Доказано , что логическая структура любой программы может быть выражена комбинацией трех базовых структур : следования , ветвления и цикла ( теорема Боэма – Якопини ). Следование – самая важная из структур . Она означает , что действия могут быть вы — полнены друг за другом . Прямоугольники , показанные на рисунке 6.2 а , могут представлять как одну единственную команду , так и множество операторов , необходимых для выполнения сложной обработки данных . Ветвление – это структура , обеспечивающая выбор между двумя альтернативами . Выполняется проверка , а затем выбирается один из путей ( см . рис . 6.2 б ). Эта структура на — зывается также ЕСЛИ – ТО – ИНАЧЕ . Каждый из двух путей ведет к общей точке слияния , так что выполнение программы продолжается независимо от того , какой путь был выбран . Цикл предусматривает повторное выполнение некоторого набора команд программы и позволяют записать длинные последовательности операций обработки данных с помощью небольшого числа повторяющихся команд . Каждый цикл либо начинается , либо заканчива — Коррадо Боэм ( р . 1923) — итальянский математик .

Источник: studfile.net

Урок 19
Моделирование и формализация

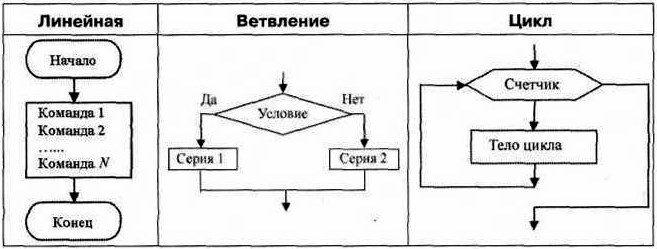
Человек при разработке и исполнении алгоритмов использует язык блок-схем. Блок-схема позволяет сделать алгоритм более наглядным и выделить в нем основные алгоритмические структуры (линейная, ветвление, цикл и др.). Человек может по блок-схеме легко проследить выполнение алгоритма, так как элементы блок-схем соединены стрелками, указывающими последовательность действий.

Элементы алгоритма изображаются на блок-схеме с помощью различных геометрических фигур (табл. 2.1), внутри которых записывается программный код.

Таблица 2.1

Блок-схемы основных алгоритмических структур

Следующая страница §2.3. Формы представления моделей. Контрольные вопросы

Cкачать материалы урока

Источник: xn—-7sbbfb7a7aej.xn--p1ai

Методика математического моделирования на компьютере

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

Просмотр содержимого документа
«Методика математического моделирования на компьютере»

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Кафедра физики, информационных технологий и методик обучения

МЕтодика математического моделирования на компьютере

Подготовил студент группы МДИ-118____________________Д.С. Винокурова

Направление подготовки 44.03.05 Педагогическое образование (с двумя профилями подготовки)

Профиль Информатика. Математика.

канд. физ.-мат. наук, доцент _________________________ Т. В. Кормилицына

Абстрактный характер теоретических построений в современных науках и появление специальных языков – это свидетельство развития познания от непосредственного контакта с окружающей человека действительностью к опосредованному её освоению, которое совершается, в частности, с помощью методов и средств моделирования. При этом не только научное познание, но и процесс обучения базируется на использовании методов информационного моделирования, так как любая передача знаний подразумевает их описание на том или ином языке и представление в той или иной форме.Поэтому знакомство школьников с методами информационного моделирования актуально для современной школы, особенно в условиях постоянно увеличивающегося объёма учебной информации, появления новых её носителей (электронные учебники, компьютерные энциклопедии) и средств доступа к ней. Учащимся необходимо осмыслить сам процесс познания, определить место в этом процессе таких познавательных приёмов, как моделирование, формализация, символизация, структуризация и др.

Мир моделей, используемых в познании, общении, практической деятельности, многообразен. В обучении важное место занимает такой класс моделей, как информационные модели. Это всевозможные формулы, графики, словесное описание, таблицы, схемы, формулировки законов, алгоритмы и пр.

Курс информатики в наибольшей степени способствует приведению в систему знаний учащихся о моделях и осознанному применению информационного моделирования в своей учебной, а затем и практической деятельности.

Модель (фр. modele , ит. modello , лат. modulus – мера, образец)

« Модель — трехмерное представление субъекта, вещи или структуры; обычно в уменьшенном масштабе».

« Модель — упрощенное описание некоей системы для дальнейших расчетов».

Оксфордский Толковый Словарь

В узком смысле — модель это «устройство, воспроизводящее, имитирующее строение и действие какого-либо другого (моделируемого) устройства в научных, производственных или практических целях».

В широком смысле — « модель — любой образ какого-либо объекта, процесса, явления, используемый в качестве его заместителя или представителя»

Советский Энциклопедический Словарь

« Модель — это новый объект, который отражает некоторые стороны изучаемого объекта или явления, существенные с точки зрения цели моделирования».

С. Бешенков, Е. Ракитина, Информатика. Систематический курс

Сперва выделим определение, которое предлагает Оксфордский Толковый Словарь. В нем приведено семь определений понятия «модель», из которых наибольший интерес представляют два: «Модель — трехмерное представление субъекта, вещи или структуры; обычно в уменьшенном масштабе» и «Модель — упрощенное описание некоей системы для дальнейших расчетов». Иными словами, авторам не удается выделить настоящие существенные признаки модели и они предлагают различные определения для различных видов моделей. Основная ошибка данных определений — их узость, объем понятия «модель» неизмеримо больше, чем предлагаемый авторами словаря.

Сходная проблема возникает и при анализе определения «модели» в Советском Энциклопедическом Словаре (СЭС). В узком смысле — это «устройство, воспроизводящее, имитирующее строение и действие какого-либо другого (моделируемого) устройства в научных, производственных или практических целях». Слово «устройство», встречающееся в определении автоматически приводит к сужению понятия «модель» как минимум до понятия «материальная модель». Тем не менее, это определение представляет собой гораздо большую ценность, чем первое определение оксфордского словаря, так как содержит внутри себя чрезвычайно важную формулировку, раскрывающую сущность моделирования — «строение и действие».

Ещё одно определение «модели» приведено в учебнике Могилёва, Пака и Хеннера: «Модель является представлением объекта в некоторой форме, отличной от формы его реального существования». Фактически, оно почти совпадает с «широким» определением СЭС, но и здесь авторы заменяют слово «отражение» синонимичным оборотом. Кроме того, использование термина «объект» может быть оправдано в рамках школьного (но не вузовского) учебника, но неприемлемо для полного определения. Современная наука занимается изучением не столько отдельных самостоятельных элементов, сколько их взаимодействий. Потому более оправдано использование в определении термина «система», который вбирает в себя как отдельные элементы, так и их отношения и связи.

В целом же, последние два определения можно признать вполне удовлетворительными и пользоваться ими.

Мир моделей многообразен. Для человека же характерно стремление систематизировать большой объём данных, чтобы «навести порядок» в разнообразии. Наиболее распространённым способом научной систематизации является классификация, то есть распределение изучаемых объектов по классам (разрядам, отделам) в зависимости от их общих признаков. Подходы к выделению классов моделей могут быть самыми различными. Рассмотрим некоторые из них.

Статические модели отображают объект в какой-то момент времени без учёта происходящих с ним изменений, как находящийся в состоянии покоя и равновесия. В этих моделях отсутствует временной параметр.

Динамические модели описывают поведение объекта во времени. Эти модели отображают процессы, происходящие с объектом во времени. В частности, таковыми являются модели функционирования и развития.

Детерминированные модели отображают процессы, в которых отсутствуют случайные воздействия.

Вероятностные (стохастические от греч. Stochasis – догадка) модели – описания объектов, поведение которых определяется случайными воздействиями (внешними и внутренними); описания вероятностных процессов и событий, характер изменения которых во времени точно предсказать невозможно.

Имитационная компьютерная модель – отдельная программа, совокупность программ, программный комплекс, позволяющий с помощью последоваетльности вычислений и графического отображения их результатов воспроизводить (имитировать) процессы функционирования объекта, системы объектов при условии воздействия на объект различных, как правило случайных, факторов.

Материальные модели иначе можно назвать предметными, физическими. Они всегда имеют реальное воплощение. Такие модели могут отражать: внешние свойства исходных объектов; внутреннее устройство исходных объектов;

Суть процессов и явлений, происходящих с объектами-оригиналами.

Материальные модели помогают узнать свойства реальных объектов и понять «механизм» сложных явлений, они часто используются в процессе обучения. Материальными моделями являются скелет человека и чучело птицы в кабинете биологии, объёмная модель Солнечной системы и макет многоступенчатой ракеты в кабинете физики и т.д.

Абстрактные модели нельзя потрогать, они не имеют вещественного воплощения. Основу таких моделей составляет информация, а такой тип моделирования реализует теоретический метод познания окружающей действительности.

Основанием для дальнейшей классификации абстрактных моделей выберем возможность их реализации и исследования при помощи компьютера. По этому признаку выделяются следующие подклассы:

• Мысленные и вербальные;
• Информационные.

• Построении модели предметной области, то есть в выделении её объектов и установлении их свойств и отношений между ними;
• Определении структуры данных;
• Определении и описании процессов и действий, допустимых в предметной области;
• Выявлении известных методов решения задачи.

• Постановка цели моделирования.
• Анализ моделирования объекта и выделение всех его известных свойств.
• Анализ выделенных свойств с точки зрения цели моделирования и определение, какие из них следует считать существенными.
• Выбор формы представления модели.
• Формализация.
• Анализ полученной модели на противоречивость.
• Анализ адекватности полученной модели объекту и цели моделирования.

• Идентификации (узнавания) объекта;
• Долговременного хранения образа.

• Её наглядного представления;
• Изучения свойств объекта;
• Выявления значимых связей;
• Изучения стабильности объекта.

• планировании, прогнозировании;
• Установлении связей с другими объектами;
• Выявлении причинно-следственных связей;
• Управлении;
• Конструировании технических устройств и т.п.

• анализ – расчленение целого на части;
• синтез – объединение частей в целое;
• абстрагирование – отвлечение от несущественных в данном конкретном случае свойств и отношений;
• обобщение – установление общих свойств и признаков объектов;
• индукция – построение общего вывода на основе частных предпосылок;
• дедукция – выведение заключения частного характера из общих посылок;
• аналогия – на основе сходства в одних признаках делается заключение о существовании сходства в других;
• моделирование – исследование модели, замещающей оригинал;
• классификация – разделение всех изучаемых объектов на отдельные группы.

• Определяется точная последовательность действий, предписанных методом решения;
• Выбирается способ записи алгоритма;
• Последовательность действий записывается по правилам этого способа.

• проведением сложных математических расчётов (численное моделирование);
• построением и исследованием наглядных и/или динамических моделей (компьютерное моделирование).

Заключение Важно помнить, что на компьютере моделируется не объективная реальность, а наши теоретические представления о ней. Объектом компьютерного моделирования являются математические и другие научные модели, а не реальные объекты, процессы, явления.

Критерием верности любого из результатов компьютерного моделирования был и остаётся натурный (физический, химический, социальный) эксперимент. В научных и практических исследованиях компьютерный эксперимент может лишь сопутствовать натурному, чтобы исследователь, сравнивая их результаты, мог оценить качество модели, глубину наших представлений о сути явлений природы. План эксперимента Схема компьютерного эксперимента План эксперимента должен чётко отражать последовательность работы с моделью. Тестирование – процесс проверки правильности построения модели.
Математическая модель выражает существенные свойства объекта или процесса на языке уравнений и других математических средств. Список литературы 1. Гарнаев, Ф. Ю. Самоучитель Visual Studio.NET 2003 – Санкт-Петербург : БХВ-Петербург, 2005. – 688 с. 2. Подлин, Ш. Освой самостоятельно программирование для Micrsoft Excel 2000. : учебное пособие. – Москва : Издательский дом «Вильямс», 2006. – 304 с. 3. Харитонова, И. А. Microsoft ACCESS 2000: Разработка приложений. – Санкт-Петербург : БХВ-Петербург, 2004. – 832 с. 4. Одинцев, И. О. Профессиональное программирование. Системный подход. – Санкт-Петербург : БХВ-Петербург, 2003. – 512 с.

Источник: kopilkaurokov.ru