Алгоритм программы в паскале

В настоящее время ЭВМ является важнейшим средством для решения инженерных, научных и управленческих задач, которые характеризуются ярко выраженной практической направленностью и значительным объёмом выполняемой вычислительной работы. Как правило, инженерные задачи решают специалисты, имеющие техническое образование, но не являющиеся профессиональными программистами. Поэтому является необходимостью знание базовых принципов алгоритмизации и основ программирования.

Несмотря на повсеместный переход на программирование под Windows, например, с использованием среды визуального программированияDelphi,Turbo Pascalсохраняет своё значение языка для первого знакомства с программированием. Это связано как с его чёткой логической структурой, так и с теми возможностями, которые позволяют использоватьТурбо Pascalдля решения разнообразных задач.

Учебное пособие предназначено для развития практических навыков работы на персональных компьютерах. Основные цели:

• получение знаний по основам алгоритмизации и программирования
• овладение основами одного из наиболее распространённых языков программирования;
• изучение и освоение основных приёмов программирования;
• программирование базовых алгоритмов различной структуры;
• освоение алгоритмов численного решения математических задач;
• получение практических навыков отладки и тестирования программ;
• ознакомление с процессом прохождения заданий при их решении на ЭВМ.

Тема 1 Алгоритмы и способы их описания

Для составления программы, предназначенной для решения на ЭВМ какой-либо задачи, требуется составление алгоритма её решения. Алгоритм– это точное предписание, которое определяет процесс, ведущий от исходных данных к требуемому конечному результату.

Программирование на Pascal. Переменные, типы данных, линейные алгоритмы. Видеокурс.

Алгоритмами, например, являются правила умножения и деления, решения алгебраических уравнений, вычисление квадратных корней и т.п. Слово алгоритм происходит отalgoritmi, являющегося латинской транслитеризацией арабского имени хорезмийского математикаIXвека аль-Хорезми. По его работам европейцы вXIIвеке познакомились с позиционной системой счисления, и в средневековой Европе алгоритмом называлась десятичная позиционная система счисления и правила счёта в ней. Применительно к ЭВМ алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности исходных данных и направленный на получение результатов, определённых этими исходными данными. Если вычислительный процесс заканчивается получением результатов, то говорят, что соответствующий алгоритм применим к рассматриваемым данным. Любой применимый алгоритм обладает следующими основными свойствами:

• результативностью– возможностью получения результата после выполнения конечного количества операций;
• определённостью – совпадении получаемых результатов независимо от пользователя и применяемых технических средств;
• массовостью – возможностью применения алгоритма к целому классу однотипных задач, различающихся конкретными значениями исходных данных.

Для задания алгоритма необходимо описать следующие элементы:

Pascal Полный курс с нуля за 4 часа

• набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов;
• правило начала;
• описание последовательности действий;
• правило окончания;
• правило извлечения результатов.

Алгоритм всегда рассчитан на конкретного исполнителя. В нашем случае таким исполнителем является ЭВМ. Для обеспечения возможности реализации на ЭВМ алгоритм должен быть описан на языке, понятном компьютеру, то есть на языке программирования. Основные способы описания алгоритмов:

• словесно-формульный;
• структурный (в виде блок-схем);
• с помощью граф-схем;
• с помощью сетей Петри.

При составлении программ чаще всего используют первые два способа. При словесно-формульномспособе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий. Пусть, например, необходимо найти значение выражения: y = 2a – (x + 6) Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:

1. Ввести значения аих;
2. Сложить хи 6;
3. Умножить ана 2;
4. Вычесть из 2асумму (х + 6);
5. Вывести yкак результат вычисления выражения.

При блок-схемномописании алгоритм изображается геометрическими фигурами (блоками), связанными по управлению линиями (направлениями потоков) со стрелками. В блоках записывается последовательность действий. Данный способ имеет ряд преимуществ. Он наиболее нагляден, поскольку каждая операция вычислительного процесса изображается отдельной геометрической фигурой.

Корме того, графическое изображение алгоритма наглядно показывает разветвление путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали. Оформление алгоритмов и распечаток текста программ должно соответствовать требованиям, установленным в системе стандартов ЕСПД (единой системе программной документации) Российской Федерации, которая устанавливает правила разработки, оформления программ и программной документации.

В ЕСПД определены и правила оформления блок-схем алгоритмов (ГОСТ 19.701-90). Операции обработки данных и носители информации изображаются на схеме соответствующими блоками. Большая часть блоков по построению условно вписана в прямоугольник со сторонами aиb. Минимальное значениеaравно 10 мм, увеличениеaпроизводится на число, кратное 5 мм. Размерb=1,5a.

Для отдельных блоков допускается соотношение междуaиb, равное 1:2. В пределах одной схемы рекомендуется изображать блоки одинаковых размеров. Все блоки нумеруются. Виды и назначение основных блоков приведено в табл. 1.1. Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводиться параллельно линиям рамки.

Стрелка в конце линии может не ставиться, если линия направлена слева направо, или сверху вниз. В блок может входить несколько линий. Из блока (кроме логического) может выходить только одна линия. Логический блок может иметь в качестве продолжения один из двух блоков, и из него выходят две линии. Если на схеме имеет место слияние линий, то место пересечения выделяется точкой.

В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить. Схему алгоритма следует выполнять как единое целое, однако, в случае необходимости, допускается обрывать линии, соединяющие блоки.

Если при обрыве линии продолжение схемы находится на этом же листе, то на одном и другом конце разорванной линии изображается специальный символ-соединитель– окружность диаметром 1,5а. Внутри парных окружностей указывается один и тот же идентификатор, в качестве которого используется порядковый номер блока, к которому направлена соединительная линия.

Если схема занимает более одного листа, то в случае разрыва линии используется межстраничный соединитель. Внутри каждого межстраничного соединителя указывается адрес – откуда и куда направлена соединительная линия. Адрес записывается в две стоки: в первой указывается номер листа, во второй – порядковый номер блока.

Блок-схема должна содержать все разветвления, циклы и обращения к подпрограммам, содержащиеся в программе. Одним из свойств алгоритма является дискретность – возможность расчленения процесса вычислений, предписанных алгоритмом, на отдельные этапы, возможность выделения участков программы с определённой структурой. Можно выделить и наглядно представить графически три простейшие структуры: выбор двух или более операций; выбор направления; повторение. Таблица 1.1. Условные обозначения блоков схем алгоритмов

Наименование	Обозначение	Функции
Процесс		Выполнение операции или группы операций, в результате которых изменяется значение, форма представления или расположение данных
Ввод-вывод		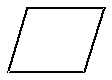Преобразование данных в форму, пригодную для обработки (ввод) или отображение результатов обработки (вывод)
Решение		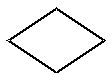Выбор направления выполнения алгоритма в зависимости от некоторых переменных условий
Предопределённый процесс		Использование ранее созданных и отдельно написанных программ (подпрограмм)
Документ		Вывод данных на бумажный носитель
Магнитный диск		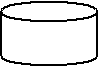Ввод-вывод данных, носителем которых служит магнитный диск
Пуск-останов		Начало, конец, прерывание процесса обработки данных
Соединитель		Указание связи между прерванными линиями, соединяющими блоки
Межстраничный соединитель		Указание связи между прерванными линиями, соединяющими блоки, расположенные на разных листах
Комментарий		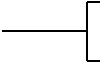Связь между элементом схемы и пояснением

Любой вычислительный процесс может быть представлен как комбинация этих элементарных структур. Соответственно, вычислительные процессы, выполняемые на ЭВМ по заданной программе, можно разделить на три основных вида: линейные; ветвящиеся; циклические. Линейнымпринято называть вычислительный процесс, в котором операции выполняются последовательно, в порядке их записи.

Каждая операция является самостоятельной, независимой от каких-либо условий. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности. Линейные вычислительные процессы имеют место, например, при вычислении арифметических выражений, когда имеются конкретные вычислительные данные и над ними выполняются соответствующие условию задачи действия.

На рис.1.1. показан пример линейного алгоритма, определяющего процесс вычисления арифметического выражения y = (b2 — ac)/(a + c) Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе – это выбор одной из нескольких последовательностей команд при выполнении программы.

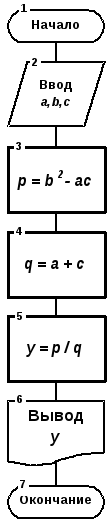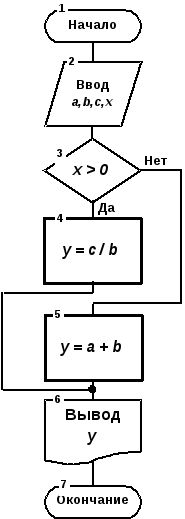Рис. 1.1. Пример линейного алгоритма	Рис. 1.2. Пример разветвляющегося алгоритма

Выбор направления зависит от заранее определённого признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений. Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей – сложным.

Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» – условие выполнено; «нет» – условие не выполнено.

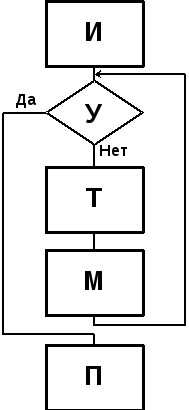
Следует иметь в виду, что хотя на схеме алгоритма должны быть показаны все возможные направления вычислений в зависимости от выполнения определённого условия, при однократном прохождении программы процесс реализуется только по одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса. На рис. 1.2. показан пример алгоритма с разветвлением для вычисления следующего выражения: 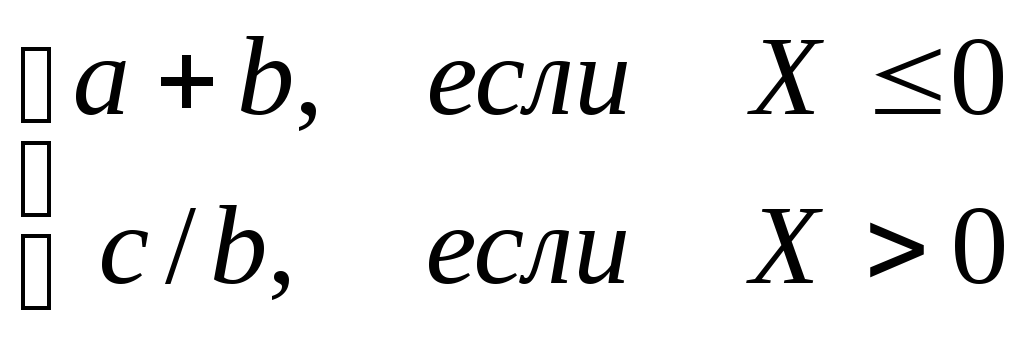Циклическиминазываются программы, содержащие циклы. Цикл – это многократно повторяемый участок программы.

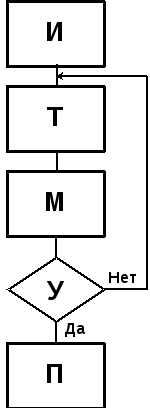а	б
Рис. 1.3. Примеры циклических алгоритмов

В организации цикла можно выделить следующие этапы:

• подготовка (инициализация) цикла (И);
• выполнение вычислений цикла (тело цикла) (Т);
• модификация параметров (М);
• проверка условия окончания цикла (У).

Порядок выполнения этих этапов, например, ТиМ, может изменяться. В зависимости от расположения проверки условия окончания цикла, различают циклы с нижним и верхним окончанием (рис.1.3). Для цикла с нижним окончанием (рис.1.3а) тело цикла выполняется как минимум один раз, так как сначала выполняются вычисления, а затем проверяется условие выхода из цикла. В случае цикла с верхним окончанием (рис.1.3б) тело цикла может не выполниться ни разу в случае, если сразу соблюдается условие выхода.

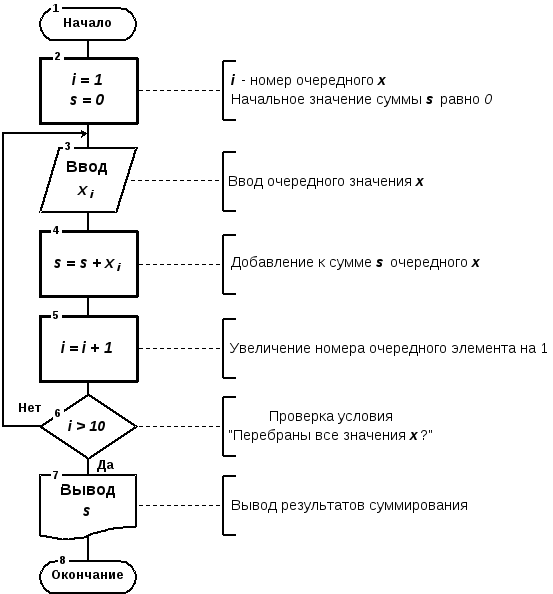Рис.1.4. Алгоритм вычисления суммы десяти чисел

Цикл называется детерминированным, если число повторений цикла заранее известно, или определено. Цикл называется итерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях. На рис.1.4 показан пример циклического алгоритма вычисления суммы десяти чисел.

Источник: studfile.net

Основы программирования в Pascal

Основы программирования в Pascal. Основы программирования в Pascal. Структура программы Линейные алгоритмы Ветвления Циклы Одномерные массивы Двумерные массивы Символьные и строковые переменные. Пример линейного алгоритма и программы в Паскале.

Uploaded on Aug 31, 2014

• Olwen Betrys
• + Follow

Download Presentation

Основы программирования в Pascal

Presentation Transcript

1. Основы программирования в Pascal
2. Основы программирования в Pascal Структура программы Линейные алгоритмы Ветвления Циклы Одномерные массивы Двумерные массивы Символьные и строковые переменные
3. Пример линейного алгоритма и программы в Паскале Задача 1.Составить алгоритм сложения двух чисел А и В, вводимых с клавиатуры. Результат сложения записать в виде переменной С. По данному алгоритму написать программу в Паскале Program summa; Var a,b,sum : integer; Begin readln(a); readln(b); sum := a + b; writeln(sum) end. Программа в Паскале Алгоритмический язык Блок-схема алг сложение цел А, В, С нач ввод А ввод В С := А + В вывод С кон начало Ввод А, В С:=A+B Вывод C конец
4. Структура программы в Паскале (минимальные требования) Program имя программы; Var имя переменной : тип; Begin операторы end. — Имя программы — Раздел описания переменных — Раздел операторов
5. Раздел описания переменных Var: ; Типы переменных: integer – целый тип (в интервале [-32.768, 32.767] – 2 байта Longint – длинный целый [-2.147.483.648, 2.147.483.647]– 4 байта real – вещественный тип — 6 байт и др.
6. Ввод исходных данных с клавиатуры read(); readln(); read(a); read(b); read(a,b);
7. Вывод данных на экран монитора write(); writeln(); Для целого типа: writeln(a); writeln(b); write(a,b); write(a,’ ‘,b); write(a:5,b:5); Для вещественного типа: writeln(a:5:2); writeln(b:7:3); write(a:7:2,b:9:3); writeln(b); (При b=1,234 на экран выведется: 1234e-3)
8. Вывод данных на экран монитора Для целого типа: writeln(‘a=‘,a); writeln(‘b=‘,b); Для вещественного типа: writeln(‘a=‘,a:5:2); writeln(‘b=‘,b:7:3); При b=1,234 на экран выведется: b= 1,234
9. Арифметические выражения в Паскале Сложение + Вычитание — Умножение * Деление / Целочисленное деление div Остаток от деления mod например: 11 div 5 = 2 2 div 3 = 0 17 div -5 = -3 -17 div 5 = -3 -17 div -5 = 3 например: 10 mod 5 = 0 10 mod 3 = 1 3 mod 5 = 3 17 mod -5 = 2 -17 mod 5 = -2 -17 mod -5 = -2
10. Приоритет операций • Минус, not • *, /, div, mod, and • +, -, or • =, <>, , =
11. Стандартные функции в Паскале
12. Этапы программирования • Постановка задачи • Математическая формализация • Построение алгоритма • Алгоритмический язык • Язык блок-схем • Составление программы на языке программирования (Паскаль) • Отладка и тестирование программы
13. Линейные алгоритмы Задача 2.Написать программу нахождения периметра прямоугольного треугольника по известным катетам a и b(a и b – целые числа, вводимые с клавиатуры). алг периметр целa, b вещc, p нач ввод a ввод b c := p:= a + b +c вывод p кон нач Периметр Ввод a Ввод b c := p:= a + b +c Вывод p кон
14. Линейные алгоритмы Задача 2.Написать программу нахождения периметра прямоугольного треугольника по известным катетам a и b(a и b – целые числа, вводимые с клавиатуры). Program perimetr; Var a,b : integer; c,p : real; Begin write(‘a=‘); readln(a); write(‘b=‘); readln(b); c := sqrt(sqr(a)+sqr(b)); p := a + b + c; writeln(‘p=‘,p:5:1); readln end.
15. Линейные алгоритмы Задача 2.Написать программу нахождения периметра прямоугольного треугольника по известным катетам a и b(a и b – целые числа, вводимые с клавиатуры). Program perimetr; Var a,b : integer; p : real; Begin write(‘a=‘); readln(a); write(‘b=‘); readln(b); p := a + b + sqrt(sqr(a)+sqr(b)); writeln(‘p=‘,p:5:1); readln end.
16. Линейные вычислительные алгоритмы Задача 2Даны переменные Xи YТребуется произвести между ними обмен значениями (№9 стр. 190) алг обмен вещ X, Y, Z нач ввод X ввод Y Z:= X X := Y Y := Z вывод X, Y кон Таблица трассировки:
17. Решение задач Записать математические выражения в Паскале и вычислить их значения при a=2, b=3: Задача. Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.
18. Домашнее задание Задачник 1§ 4.4.1стр. 218-222; № 1, 13, 28

Источник: www.slideserve.com

Программирование линейных алгоритмов

Паскаль (англ. Pascal) — процедурный язык структурного
программирования. Является одним из наиболее известных языков
программирования, используется для обучения программированию
в старших классах и на первых курсах вузов, является базой для
ряда других языков.

3. Структура программы на Паскале

4. Типы данных, определенных в Паскале

Паскаль характеризуется большим разнообразием типов данных.
Каждый тип имеет свой идентификатор.
Идентификатор
Длина (байт)
Диапазон значений
Операции
integer
byte
2
1
-32768..32767
0..255
+, -, /,*, Div, Mod, >=, ,
+, -, /,*, Div, Mod, >=, ,
word
2
0..65535
+, -, /,*, Div, Mod, >=, , >
shortint
1
-128..127
+, -, /,*, Div, Mod, >=,,
longint
4
-214748364..214748364
+, -, /,*, Div, Mod, >=, ,

5. Основные правила записи программ на Паскаль

1) Программа на языке Паскаль – это последовательность операторов, записанных по
правилам языка Паскаль. Каждый оператор, как правило, вводится с новой строки.
Операторы отделяются друг от друга точкой с запятой. После оператора Begin и перед End
точку с запятой можно не ставить.
2) Программа состоит из основного блока, в котором находятся операторы, и разделов
описаний.
Описываться должны все переменные и константы, которые встретятся в
тексте, метки операторов, процедуры и функции, введенные пользователем, и другие
объекты программы.
3) Перед первым оператором в начале основного блока обязательно ставится оператор
Begin, после последнего оператора –оператор End с точкой на конце.
4) Для облегчения чтения программа может иметь комментарии. Комментарии
выделяются фигурными скобками <> или(*
*) .
5) По традиции программы на Паскале пишутся с отступами от левого края. Запись
программы «лесенкой» облегчает чтение и отладку программ и является признаком
хорошего стиля программирования.

6. Линейный алгоритм

Алгоритм – это понятное и точное предписание исполнителю выполнить конечную
последовательность команд, приводящую от исходных данных к искомому
результату.
Линейный алгоритм — набор команд (указаний), выполняемых последовательно
друг за другом. Эти команды выполняются однократно и представляют собой цепь
простых действий.
В линейной программе могут присутствовать только операторы присваивания,
ввода, вывода и обращения к процедурам.
Алгоритм обладать свойствами: результативность, дискретность (пошаговость),
определённость, понятность, выполнимость, массовость.
Формы представления алгоритмов:
словесная (записи на естественном языке);
графическая (изображения из графических символов);
псевдокоды (полуформализованные описания алгоритмов на условном
алгоритмическом языке);
программная (тексты на языках программирования).

7. Оператор присваивания

Присваивание — действие, в результате которого переменная
величина получает определенное значение.
Оператор присваивания имеет следующий формат:
:=
Например:
1) x := 2*a+sqrt (b)
2) b := (x > y) and (k<>0)

8. Оператор ввода

Ввод — передача данных с внешнего устройства в ОЗУ.
Операция ввода называется чтением и выполняется с помощью
оператора Read.
Ввод с клавиатуры производится путем обращения к стандартной
процедуре Read в следующем формате:
Read ()
Например:
Read (a, b, c, d)

9. Оператор вывода

Вывод – передача данных из ОЗУ на внешнее устройство.
Вывод называется записью, и для его выполнения используется
оператор Write.
Вывод на экран производится по оператору обращения к
стандартной процедуре:
Write ()
Например:
Write (‘Сумма’, А, , А+В)

10. Поэтапное решение задачи

Задача 1. Находим число представляющее квадрат данного в задаче
натурального числа — 256.
Этап решения
Описание
1. Постановка задачи – определение исходных
данных и искомых результатов
дано а – число, которое является
целочисленным типом данных,
найти число b, которое является квадратом а.
2. Формализация – переход к задаче обработки
некоторый знаковой системы (математ. задаче) В := a*а

11.

Этап решения
3. Построение алгоритма – определение структуры
алгоритма, последовательность команд
Описание
Начало
А, B
B=А*А
B
Конец

12.

Этап решения
4. Составление программы – запись и отладка
программы на языке программирования
5. Тестирование – экспериментальное
доказательство правильности алгоритма и
работоспособности программы
Описание
Рrogram SqrOfNum;
Var a, b: word;
Degin
readln (a);
b := a * a;
writeln (b)
End.

Источник: ppt-online.org