Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Внутри блока дается описание соответствующего действия.
Такое графическое представление называется схемой алгоритма или блок-схемой.
Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации.
Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему – набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации“. Здесь форма представления алгоритма смешивается с самим алгоритмом.
Информатика 9 класс. Построение алгоритмов в графическом виде
Принцип программирования “сверху вниз” требует, чтобы блок-схема поэтапно конкретизировалась и каждый блок “расписывался” до элементарных операций. Но такой подход можно осуществить при решении несложных задач. При решении сколько-нибудь серьезной задачи блок-схема “расползется” до такой степени, что ее невозможно будет охватить одним взглядом.
Блок-схемы алгоритмов удобно использовать для объяснения работы уже готового алгоритма, при этом в качестве блоков берутся действительно блоки алгоритма, работа которых не требует пояснений. Блок-схема алгоритма должна служить для упрощения изображения алгоритма, а не для усложнения.
При решении задач на компьютере необходимо не столько умение составлять алгоритмы, сколько знание методов решения задач (как и вообще в математике). Поэтому изучать нужно не программирование как таковое (и не алгоритмизацию), а методы решения математических задач на компьютере. Задачи следует классифицировать не по типам данных, как это обычно делается (задачи на массивы, на символьные переменные и т. д.), а по разделу “Требуется”.
Схема — это графическое представление алгоритма, дополненное элементами словесной записи. Каждый пункт алгоритма отображается на схеме некоторой геометрической фигурой-блоком (блочным символом), причем различным по типу выполняемых действий блокам соответствуют различные геометрические фигуры, изображаемые по ГОСТу.
ГОСТ 19.701-90 (обозначение символов соответствует международному стандарту ИСО 5807-85) распространяется на условные обозначения (символы) в схемах алгоритмов, программ, данных и систем и устанавливает правила выполнения схем, используемых для отображения различных видов задач обработки данных и средств их решения.
В таблице 1 приведены наиболее часто употребляемые блоки и даны пояснения к ним [1,2].
Графические символы на схеме соединяются линиями потока информации. Основное направление потока информации идет сверху вниз и слева на право (стрелки на линиях могут не указываться). В других случаях применение стрелок обязательно. По отношению к блоку линии потока могут быть входящими или выходящими. Количество входящих линий для блока принципиально не ограничено.
Как БЫСТРО изучить АЛГОРИТМЫ и научиться решать задачи? Книги, сайты, инструменты
Выходящая линия может быть только одна. Исключение оставляют логические блоки, имеющие не менее двух выходящих линий потока, каждая из которых соответствует одному из возможных исходов проверки логического условия, а также блоки модификации.
Блок вычислительный процесс применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок.
Таблица 1. Условные графические обозначения, применяемые при составлении схем алгоритмов
Блоки ввода – вывода
Логический блок используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок предопределенный процесс используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Блок модификация используется для организации циклических конструкций. Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
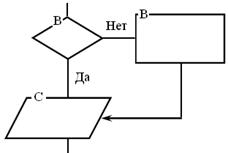
При большом количестве пересекающихся линий, большой их длине и многократных изменениях направления схемы становится малонаглядной. В этих случаях допускается разрывать линии потока информации, размещая на обоих концах разрыва специальный символ «соединитель» (рис. 1). Внутри поля соединителей, отмечающих разрыв одной и той же линии, ставится одинаковая маркировка отдельной буквой или буквенно-цифровой координатой блока, к которому подходит линия потока.
Рис. 1. Соединитель
Если схема располагается на нескольких листах, переход линий потока с одного листа на другой обозначается с помощью символа «межстраничный соединитель» (рис. 2). При этом на листе с блоком – источником соединитель содержит номер листа и координаты блока-приемника, а на листе с блоком–приемником – номер листа и координаты блока – источника.
Рис. 2. Межстраничный соединитель
Внутри блоков и рядом с ними делают записи и обозначения (для уточнения выполняемых ими функций) так, чтобы их можно было читать слева направо и сверху вниз независимо от направления потока. Например, на (рис. 3) вид 1 и вид 2 читаются идентично.
Порядковые номера блоков проставляют в верхней части графического символа в разрыве его контура (рис. 1 и 4).
При выполнении схем алгоритмов необходимо выдерживать минимальное расстояние 3 мм между параллельными линиями потоков и 5 мм между остальными символами. В блоках приняты размеры: 
=10, 15, 20 мм; 
=1.5 (рис.3). Если необходимо увеличить размер схемы, то допускается увеличивать на число кратное пяти.
Схема является исключительно наглядным и простым способом представления алгоритма. При этом не накладывается никаких ограничений на степень детализации в изображении алгоритма. Выбор ее целиком зависит от программиста. Но, нужно иметь ввиду, что излишне общий характер схемы нежелателен из-за малой информативности, а очень детальная схема проигрывает в наглядности.
Для особенно сложных и больших алгоритмов, целесообразно составлять несколько схем различных уровней детализации. Схема 1-го уровня отображает весь алгоритм целиком. Схемы 2-го уровня раскрывают логику отдельных блоков схемы 1-го уровня. При необходимости могут быть составлены схемы последующих уровней с еще большей степенью детализации. Такое пошаговое уточнение схемы алгоритма составляет сущность метода нисходящего проектирования, который, в свою очередь, является основой структурного программирования.
Псевдокод
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов. Он занимает промежуточное место между естественным и формальным языками [7].
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. В псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В псевдокоде как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются. Единого определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных конструкций.
Алг Нахождение суммы;
Источник: studopedia.ru
ГРАФИЧЕСКИЙ СПОСОБ ЗАПИСИ АЛГОРИТМА. БЛОК-СХЕМА.
Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой.
Блок-схемой называется наглядное изображение алгоритма, когда отдельные действия (этапы алгоритма) изображаются при помощи различных геометрических фигур (блоков), а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющие эти фигуры.
1. Начало и конец алгоритма:  2. Блок присваивания (процесс):  3. Ввод данных с клавиатуры:  4. Вывод информации на экран (на печать):  5. Блок ветвления (проверки условия):  |
6. Подготовка данных — внутри записывается имя переключателя и условия его модификации.  7. Блок цикла с параметром: 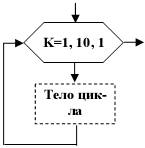 8. Нумерация блоков, значок перехода на блок с указанным номером:  9. Комментарии — для добавления описательных комментариев или пояснительных записей в целях объяснений или примечаний: 
|
ОСНОВНЫЕ СТРУКТУРЫ АЛГОРИТМОВ
Основные структуры алгоритмов — это ограниченный набор блоков и стандартных способов их соединения для выполнения типичных последовательностей действий.
Основные структуры алгоритмовиспользуются при структурном подходе к разработке алгоритмов и программ, предполагающем использование нескольких основных структур, комбинация которых дает все многообразие алгоритмов и программ.
По используемой структуре управления вычислительным процессом алгоритмы классифицируют следующим образом:
- линейной структуры;
- разветвляющейся структуры;
- циклической структуры;
- смешанной (комбинированной) структуры.
Алгоритм линейной структуры — алгоритм, в котором все действия выполняются последовательно друг за другом.
Алгоритм разветвляющейся структуры — алгоритм, в котором в зависимости от выполнения некоторого логического условия вычислительный процесс должен идти по одной или другой ветви. Можно выделить несколько разветвляющихся структур, отличающихся друг от друга числом ветвлений и наличием выполняемых действий: разветвление, обход, множественный выбор.
Структура разветвления (рис. а)предполагает проверку условия и в зависимости от истинности условия будет выполняться «Действие 1» (если условие принимает значение «истина») или «Действие 2» (если условие принимает значение «ложь»).
Структуру обхода (рис. б) можно считать частным случаем разветвления, когда в одной из ветвей обработки данных не содержится никаких действий.
Множественный выбор (рис. в) предполагает возможность развития вычислительного процесса по одному из нескольких направлений. В процессе решения данной алгоритмической схемы будет выполняться та ветвь обработки данных, для которой вычисленное в блоке «Решение» значение переменнойDсовпадет со значением одной из константDi, D2, . D.
Алгоритм циклической структуры — алгоритм, содержащий многократно выполняемые участки вычислительного процесса, называемые циклами. Если алгоритм содержит цикл, внутри которого размещен один или несколько других циклов, то такой алгоритм называется алгоритмом со структуройвложенных циклов.
Существуют два основных вида циклических алгоритмов: циклические алгоритмы с предусловием (цикл «ПОКА»), циклические алгоритмы с постусловием (цикл «ДО»). Они отличаются друг от друга местоположением условия выхода из цикла.
Цикл с предусловием (рис. а) начинается с проверки условия выхода из цикла. Если оно ложно, то выполняются те действия, которые составляют тело цикла. В противном случае, если логическое выражение истинно, то этот цикл прекращает свои действия. Особенность этого цикла состоит в том, что цикл может не выполниться ни разу, если условие выхода при первой же проверке даст истинный результат.
Цикл с постусловием (рис. б) функционирует иначе. Сначала выполняется один раз те действия, которые составляют тело цикла, затем проверяется логическое выражение, определяющее условие выхода из цикла. Если условие выхода истинно, то цикл с постусловием прекращает свою работу, в противном случае происходит повторение действий, указанных в цикле. Этот цикл всегда выполняется хотя бы один раз, так как первая проверка условия выхода происходит после выполнения действий, составляющих тело цикла.
Дата добавления: 2018-04-15 ; просмотров: 3187 ; Мы поможем в написании вашей работы!
Источник: studopedia.net
Energy
education
Информация — сведения, воспринимаемые человеком и (или) специальными устройствами как отражение фактов материального или духовного мира в процессе коммуникации (ГОСТ 7.0-99).
2. Теория алгоритмизации
Слово «алгоритм» происходит от имени выдающегося математика средневекового Востока Мухаммеда аль-Хорезми (787 – 850). Около 852 года он написал книгу, в которой им были предложены приёмы выполнения арифметических вычислений с многозначными числами.
В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик (имя его неизвестно) дал ей название Algoritmi de numero Indorum («Алгоритми о счёте индийском»). Слово algorism (или algorismus) обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многин европейские языки.
Таким образом, сочинения по искусству счёта стали называться алгоритмати.
В 1684 году Готфрид Лейбниц в сочинении «Nova Methodvs pro maximis et minimis, itemque tangentibus…» впервые использовал слово «алгоритм» (Algorithmo) в ещё более широком смысле: как систематический способ решения проблем дифференциального исчисления.
Пользовался словом «алгоритм» и ещё один выдающийся математик – Леонард Эйлер, одна из работ которого так и называется – «Использование нового алгоритма для решения проблемы Пелля». Здесь видно, что Эйлер уже понимает алгоритм в ещё более широком смысле, а именно: как синоним способа решения задачи.
В 30-е годы XX века возникает научное направление «Теория алгоритмов», предметом исследования которого стала разработка универсальной алгоритмической модели. Наибольший вклад в теорию алгоритмов внесли английский математик Алан Тьюринг и русский математик Андрей Марков.
Алан Тьюринг в 1935-1936 годах создаёт теорию «логических вычисляющих машин». Разработанная им «машина Тьюринга» стала обязательной частью обучения будущих математиков и компьютерщиков. На одной из лондонских гостиниц мемориальная доска гласит: «Здесь родился Алан Тьюринг (1912 — 1954), взломщик кодов и пионер информатики».
Андрей Марков в 1947 году ввёл понятие «нормального алгоритма» и впервые систематически и строго построил общую теорию алгоритмов. Современные языки символьной обработки информации (Пролог) берут своё начало от нормальных алгоритмов Маркова.
Понятие алгоритма так же фундаментально для информатики, как и понятие информации. Поэтому в нём очень важно разобраться. Единого «истинного» определения понятия «алгоритм» не существует. Вот лишь некоторые из предлагаемых определений:
«Алгоритм – это всякая система счислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи». (А. Колмогоров)
«Алгоритм – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату». (А. Марков)
«Алгоритм – строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд». (Н. Угринович)
При изучении информатики чаще всего используют следующее определение алгоритма:
Алгоритм – понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящую от исходных данных к искомому результату.
Каждый человек в повседневной жизни выполняет огромное количество алгоритмов.
- Алгоритм «Заварка чая» Вскипятить воду в чайнике
- Положить в пустую чайную чашку пакетик чая
- Залить чашку горячей водой
- Подождать 1 минуту
- Вытащить пакетик
- Положить в чашку 2 чайных ложки сахара
- Размешать сахар
- Алгоритм «Приготовить яичницу» Достать яйцо и масло
- Включить плиту
- Поставить сковороду на плиту
- Растопить на сковородке масло
- Взять нож
- Разбить ножом яйцо над сковородкой
- Выбросить скорлупу в мусорное ведро
- Жарить яичницу 5 минут
- Выключить плиту
Для разработки алгоритма необходимо иметь исходную информацию (данные) и представлять конечный результат (цель).
Полный набор данных – необходимый и достаточный набор данных для решения поставленной задачи (получения искомого результата).
Исполнитель алгоритма – это объект или субъект, для управления которым составлен алгоритм.
В качестве исполнителей могут быть как живые существа, так и технические устройства. В частности, автоматическим исполнителем алгоритмов по обработке информации является компьютер.
Очень часто исполнителем алгоритмов является сам человек. Мы выполняем алгоритмы, когда переходим улицу, готовим еду, делаем уроки, звоним по телефону и т.д.
Но между человеком и автоматическим устройством есть существенная разница. Если для человека имеют значение не только указания, которые даны в алгоритме, но и большой фактор заложен в степени эмоциональности изложения, то для компьютера или другого устройства имеет значение – понимает он данную команду или нет. Выполнив необходимые действия, алгоритмическое устройство прекращает работу.
Поэтому исполнителя, выполняющего команды определённого алгоритма без анализа действий и ситуаций, называют формальным исполнителем.
Иными словами работа исполнителя состоит в последовательном формальном выполнении команд алгоритма, что не предполагает анализа правильности их построения, а также результата выполнения.
Пример. Исполнители алгоритмов:
 |
 |
 |
 |
 |
| Компьютер | Солдат | Телевизор | Дрессированный лев | Автомобиль |
Исполнителя алгоритма характеризует среда его «обитания» и система команд исполнителя (СКИ).
Среда исполнителя – обстановка, в которой функционирует исполнитель.
Система команд исполнителя (СКИ) – это вся совокупность команд, которую может выполнить исполнитель.
СКИ считается полной, если содержит весь минимально-необходимый набор команд, позволяющий построить любой алгоритм в том классе задач, на который ориентирован исполнитель.
Определённая последовательность действий исполнителя всегда применяется к некоторым исходным данным. Например: для приготовления блюда по кулинарному рецепту нужны соответствующие продукты (данные). Для решения математической задачи (решение квадратного уравнения) нужны исходные числовые данные (коэффициенты и уравнения).
Любой алгоритм должен удовлетворять четырём основным свойствам:
- Конечность
- Дискретность
- Понятность
- Точность
Конечность алгоритма означает, что за конечное число шагов должен быть получен результат. Поэтому иногда это свойство называют результативностью.
Пример. Пусть имеется последовательность команд:
- Конечность алгоритма Взять книгу
- Открыть первую страницу
- Пока не конец книги выполнить следующие действия:
- Прочитать текст
- Перелистнуть книгу на следующую страницу
- Прочитать текст
- Открыть первую страницу
Легко догадаться, что данная последовательность команд будет выполняться бесконечно и поэтому алгоритмом не является.
Дискретность означает, что алгоритм должен быть разбит на последовательность отдельно выполняемых шагов.
Пример. Пусть необходимо решить следующий пример: (80+10)-5*(3+5)=
Запишем алгоритм решение примера, разбив его на шаги:
- Дискретность алгоритма Вычислить 80+10
- Вычислить 3+5
- Умножить 5 на результат предыдущего действия
- Вычесть из результата 1-го действия результат 3-го действия
В результате выполнения алгоритма получим 50. Алгоритм будет выполняться только при условии одного действия за раз.
Понятность алгоритма означает, что алгоритм должен содержать только те команды, которые входят в СКИ.
Пример. Рассмотрим алгоритм:
- Понятность алгоритма Пойти на кухню
- Вскипятить чайник
- Насыпать в чашку 1 чайную ложку кофе
- Положить в чашку 3 чайных ложки сахара
- Налить полную чашку кипячёной воды
Очевидно, что он легко может быть выполнен 10-летней девочкой, которая понимает все команды, входящие в данный алгоритм. Однако, для 10-месячного малыша данный алгоритм будет непонятен.
Точность алгоритма означает, что любая его команда должна определять однозначное действие исполнителя. Иными словами, алгоритм не должен быть рассчитан на принятие каких-либо самостоятельных решений исполнителем.
Пример. Рассмотрим следующий алгоритм, описывающий, как добраться до стадиона:
- Точность алгоритма Идти прямо
- Повернуть
- Идти прямо
- Сесть на автобус
- Доехать до остановки «Стадион»