Методическое пособие практического занятия по теме: «Алгоритм перевода целых чисел из одной системы счисления в другую » , может быть использовано обучающимися, как обобщение и закрепление знаний по данной теме.
Структура занятия построена так, что обучающийся в начале занятия имеет возможность оценить свои знания по данной теме, проверить кроссворд домашнего задания, ответить на вопросы по актуализации опорных знаний, изучить и закрепить основные правила выполнения перевода из одной системы счисления в другую и проконтролировать степень усвоения с помощью выполнения заданий аудиторной самостоятельной работы.
Учебные цели занятия развивают навыки по самостоятельной работе с материалами занятия и формируют навыки ответственности за проделанную работу. Преподавателем предусмотрены разноуровневые задания практической работы, которые позволяют лучше закрепить материал. Проверка заданий самостоятельной работы осуществляется самоконтролем, используя эталоны ответов. На этапе закрепления изученного материала студентам предлагается выполнить самостоятельную работу по инструкциям, прилагаемым к каждому заданию.
Java. Системы счисления. Алгоритм перевода в произвольную систему счисления.
Методическое пособие по теме: «Алгоритм перевода целых чисел из одной системы счисления в другую » , учебной дисциплины «Информатика» составлено в соответствии с требованиями Федерального государственного образовательного стандарта к минимуму содержания и уровню подготовки выпускника по специальности 060101 Лечебное дело по программе углубленной подготовки, рабочим учебным планом колледжа и рабочей программой учебной дисциплины.
Методическое пособие создано с целью оказания методической помощи студенту для эффективного формирования знаний, умений и практических навыков по теме: «Алгоритм перевода целых чисел из одной системы счисления в другую » , а также с целью дополнения учебного материала для более эффективного его усвоения.
Цель создания методического пособия:
- Обобщение, систематизация и углубление знаний учащихся по данной теме:
- история систем счисления разных стран и цивилизаций;
- решение поставленных задач на примере счета в различных системах счисления;
- совершенствование умений и навыков в переводе чисел из одной системы счисления в другую;
Для достижения поставленной цели необходимо решить задачи:
- Основные единицы измерения количества информации.
- Системы счислений используемые в компьютере;
- О двоичном представлении информации в компьютере;
- Правила перевода чисел из одной системы счисления в другую;
- Переводить числа из одной системы счисления в другую;
- Перечислять особенности и преимущества двоичной формы представления информации;
Продолжить процесс формирования эстетических чувств гармонии и красоты, путем познания стройности и гармонии информационных систем
Формирование у студентов навыков самостоятельной работы, способности участия в коллективной мыслительной деятельности
СИСТЕМЫ СЧИСЛЕНИЯ для новичков
Сегодня мы с вами продолжим изучать системы счисления, которые использовались в разное время различными цивилизациями. Мы должны также познакомиться с правилами перевода чисел из одной системы счисления в другую.
Давайте докажем, что действительно только мыслящий человек может осилить информатику.
То, что мы знаем – ограничено, а то, что мы не знаем – бесконечно.
Вся информация, которая нас окружает, представлена в аналоговой форме (книги, музыка, речь, рисунки и т.д.), а для компьютера важна информация цифровая.
Этап: «Контроль исходного уровня знаний»
У каждого из Вас на столе лежит папка с учебно-методическими материалами занятия. Все материалы будут использованы по ходу проведения занятия, они помогут нам подвести итог ваших умений и навыков, приобретенных на данном занятии.
При выполнении домашнего задания, с какими трудностями вы столкнулись? Я отвечу на все ваши вопросы. Затем все вместе решим кроссворд, заполняя таблицу кроссворда на экране. На экране появится кроссворд с правильными вариантами ответов, каждый из Вас оценит свою работу в баллах и проставит их в оценочный лист.
С этим заданием Вы справились. Молодцы!
Вопросы по горизонтали:
- Система счисления, использовавшаяся в Древней Руси
- Позиционные системы счисления имеют основание и …?
- Непозиционная система счисления широко известная в наша дни?
- Единица измерения количества информации
- Кнопка на клавиатуре
- Где возникла современная десятичная система счисления?
Вопросы по вертикали:
- Родина шестидесятеричной системы счисления
- Какая система счисления возникла 3-5 тыс. лет назад?
- Как зазываются цифры, которыми мы пользуемся?
Источник: nsportal.ru
Алгоритм перевода целого числа из десятичной системы счисления в систему счисления с произвольным основанием (р)
Для перевода целого числа нужно делить его на произвольное основание (р) до получения целого частного. Полученный остаток, в том числе ноль, будет младшим разрядом числа в новой системе счисления. Полученное частное нужно опять разделить на произвольное основание (р) до получения целого частного и продолжать этот процесс до тех пор, по частное не станет нулем.
Полученные остатки будут разрядами числа в новой системе счисления. Число в системе счисления с основанием р получается выписыванием в обратно порядке полученных остатков. Все действия выполняются по правилам десятичной системы счисления.
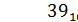
Пример:
39:2=19 целых и 1 в остатке, значит =1
19:2=9 целых и 1 в остатке, значит =1
9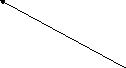
:2=4 целых и 1 в остатке, значит
=1
4:2=2 целых и 0 в остатке, значит =0
2:2=1 целых и 0 в остатке, значит 
=0, результат от деления
=1
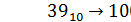
Ответ:
Алгоритм перевода целого числа из системы счисления с произвольным основанием (р) в десятичную систему счисления
Для перевода из системы счисления с основанием р в десятичную систему счисления нужно представить число в виде многочлена и вычислить значение этого многочлена по правилам арифметики десятичной системы счисления
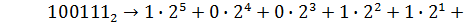
Пример: Перевести число 100111 из двоичной в десятичную систему счисления:
Удобно вычислять значение многочлена, используя схему Горнера
N
=
,
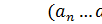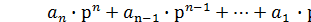
Тогда N==
=(…(
)
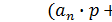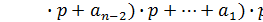
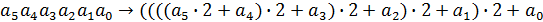
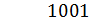
((((1∙2+0)∙2+0)∙2+1)∙2+1)∙2+1
Источник: studfile.net
Алгоритмы перевода чисел в различные системы счисления и их реализация на PHP
В рамках курса «Введение в системный анализ» было получено задание на перевод своей фамилии в различные системы счисления (2, 3, 8, 9, 10, 256, факториальную и фибоначчиевую). Вобщем-то ничего особо сложно, если бы не 24-х разрядное число, которое давала моя фамилия и отказывались считать Excel и ручные калькуляторы (да, стандартный calc.exe считает, но это то еще занудство). Поэтому я, ранее пользовавшийся только VBA и UOpilot’ом, и не найдя в сети единого решения данной задачи и реализации какой-либо его части на PHP, решил познакомиться c PHP и Arbitrary Precision Mathematic. Следует отметить, что в эту сторону меня направил комментарий unnamed777 в этой статье, за что ему большое спасибо.
Подробнее под катом.
Текст задания:
«Пользуясь кодовой страницей 1251 (или 0866), запишите свою фамилию в виде числа в 256-чной (байтовой) системе счисления. Заменив каждую 256-чную цифру двумя 16-чными (»дампом»), переведите это число в шестнадцатеричную систему счисления. Затем (уже из шестнадцатеричной) переведите его в системы счисления с основаниями 8, 2, 3, 9, 10.
Наконец, переведите это число в факториальную и фибоначчиевскую системы счисления.
Все нужные определения Вы легко найдёте по ссылкам с www.mashavph.narod.ru/Cheb02/term.htm .».
Теория вопроса:
Поскольку целью данного раздела является прежде всего понимание принципов выполнения упражнения по системам счисления (далее СС) в курсе «Введение в системный анализ», здесь будут рассмотрены алгоритмы преобразования лишь между интересующими нас в пределах данной работы СС, причем только в установленных заданием направлениях.
Итак:
1
Переводы между СС с основаниями x^n, где x — константа, удобно выполнять в 2 шага: переводя сначала в СС с основанием x^1, потом в целевую. Последовательно разбиваем цифры числа на группы по n знаков, где n — это степень x для СС с большим основанием. Разбиение и перевод начинаем с конца числа.
Далее используя калькулятор/таблицы и не нарушая порядка чисел и цифр в них, последовательно переводим получившиеся элементы массива в целевую (в этой паре СС) СС. Результат записываем в строку, сохраняя последовательность чисел и цифр в них. Пруфлинк.
2
От любой позиционной СС можно перейти к 10-й СС используя схему Горнера. Пример для числа MNOP в СС с основанием n: MNOPn = (((M*n)+N*n)+O*n)+P = %чего-то_там%10, что эквивалентно MNOPn = M*(n^(m-1))+N*(n^(m-2))+. +P*(n^0) = %чего-то_там%10, где m — кол-во цифр в исходном числе для исходной СС (так число 103070256 состоит из 2-х цифр). Пруфлинк 1. Пруфлинк 2.
3
От 10-й СС можно перейти к любой другой позиционной СС используя следующий метод: итерационно делим число в 10-й СС на основание целевой СС пока 10-е число не обратится в 0. При этом остатки от деления записываем в обратном порядке (дописывая к результату слева и сохраняя порядок цифр в них) и работать продолжаем с целым частным. Итоговый/ая массив/строка чисел и будет исходным числом, отображенным в целевой СС. Пруфлинк 1. Пруфлинк 2.
4
Поскольку факториальная СС условно позиционная, перевод из 10-й СС в факториальную можно считать частным случаем п.3 с той лишь разницей, что в качестве делителей мы будем последовательно использовать числа следующего ряда: 2, 3, 4, 5, 6, 7… Т.е. 23910 = 1 4 3 2 1(остатки деления) = 14321. Пруфлинк 1. Пруфлик 2.
5
Ряд Фибоначчи — это числовой ряд, где каждый следующий элемент равен сумме двух предыдущих. Любое натуральное число можно представить в виде суммы нескольких членов последовательности Фибоначчи.
Такое представление будет неоднозначным, но если наложить дополнительное условие, что в представлении нет двух соседних членов последовательности Фибоначчи, то представление становится единственным. Таким образом к фибоначчиевой СС от 10-й проще всего перейти последовательно вычитая из 10-го числа числа ряда Фибоначчи, начиная с заведомо большего чем 10-е число и записывая логическую характеристику результата этой операции в итоговый ряд.
Если при вычитании из 10-го числа числа ряда Фибоначчи получается отрицательное значения — записываем «0» и продолжаем работать с этим же 10-м числом. Если положительное — записываем «1» и далее уже работаем с полученной разностью. Все нули до первой единицы слева можно отбросить. Пример: для числа 23910 и ряда 377 233 144 89 55 34 21 13 8 5 3 2 1 получим 100000001001ф. Пруфлинк.
Примечания:
— Все вышеизложенные операции справедливы для множества натуральных чисел.
— В пунктах 2, 3, 4 и 5 расчеты выполняются по правилам десятичной арифметики.
— Хотя можно встретить описания ряда Фибоначчи как 1, 1, 2, 3, 5, 8.. и 0, 1, 1, 2, 3, 5, 8.., для расчетов в качестве базиса фибоначчиевой СС, как правило, используется ряд 1, 2, 3, 5, 8., что подтверждается в том числе и материалами данных сайтов.
Далее была реализация задуманного на PHP:
$Surname = $_REQUEST[«Surname»];
$dlina= strlen ($Surname);
if ($dlina > 12) echo «Не верю!»;
>elseif ($dlina > 0) echo «Фамилия: $Surname
«;
echo «Фамилия согласно кодировке Windows-1251:
«;
////////////////////////////////////3,8,9
function to($chis, $osn) <
global $st8,$st3,$st9;
$divres = array();
While ($chis > 0) $prevchis = $chis;
$chis = bcdiv ($chis, $osn);
$ost = bcmul ($chis, $osn);
$ost = bcsub ($prevchis, $ost);
array_unshift($divres,$ost);
>
while (list(,$val) = each($divres)) if ($osn == 3) $st3 .= $val;
>
elseif ($osn == 8) $st8 .= $val;
>
elseif ($osn == 9) $st9 .= $val;
>
>
>
//////////////////////////////////////10 в факториал
function ttfact($chis) global $stfact;
global $stf210;
$facdivres = array();
$osn = 2;
While ($chis > 0) $prevchis = $chis;
$chis = bcdiv ($chis, $osn);
$ost = bcmul ($chis, $osn);
$ost = bcsub ($prevchis, $ost);
//echo $ost;
//$facdivres .= $ost;
array_unshift($facdivres,$ost);
$osn++;
>
while (list(,$val) = each($facdivres)) $stfact .= «$val «;
$i—;
>
>
function lfact($num) < // вычисляем факториал переданного числа
for ( $i = $num — 1; $i > 0; $i—) $num = bcmul ($i,$num);
>
return $num;
>
///////////////////////256,16,10,2
$i=0;
$st10 = 0;
while ($i <$dlina)< // в цикле преобразуем каждый символ в ASCII код
$kus = $Surname;
$ordd = (ord ($kus));
echo «$kus — $ordd
«;
$kus = ord ($Surname); // kus в 256
$st256 .= $kus; //собираем 256-ю строку
$st10 = bcadd ($st10, $kus); // первый $st10 должен быть 0
$st10 = bcmul ($st10, ‘256’); // Самый окончательный результат разделить на $osn
$kus = dechex ($kus); // kus в 16
$st16 .= $kus; // собираем 16-ю строку
$kus = base_convert ($kus,16,2); // kus в 2
$st2 .= $kus; //собираем двоичную строку
$i++;
>
$st10 = bcdiv ($st10, ‘256’);
$i = 0;
////////////////////////////фибоначчи
$stfib = «»;
function fibonacci($n) global $arr;
if ($n < 3) return 1;
>else $n1 = $n — 2;
$n2 = $n — 3;
return bcadd ($arr[$n1], $arr[$n2]);
>
>
for ($n = 1; $n <= 150; $n++) $nar = $n — 1;
$arr[$nar] = fibonacci($n);
>
//////////////////////////вывод результатов
echo «Числов 256-чной СС: $st256»;
echo «
Число в 16-чной СС: $st16″;
echo «
Число в 2-чной СС: $st2″;
to ($st10,3);
echo «
Число в 3-чной СС: $st3″;
to ($st10,8);
echo «
Число в 8-чной СС: $st8″;
to ($st10,9);
echo «
Число в 9-чной СС: $st9″;
echo «
Число в 10-чной СС: $st10 (Перевод выполнен по схеме Горнера)»;
ttfact ($st10);
echo «
Число в факториальной СС: $stfact (Переводим из 10-й)»;
arsort ($arr);
reset ($arr);
echo «
Жирным выделенны числа ряда, задействованные для перевода из 10-й СС в СС на основе ряда Фибоначчи»;
while (list($key,$val) = each($arr)) if ( (bccomp($st10, $val)) == -1) if ($key == 0) < // хитрая фигнюшка
goto fg;
>
echo «
$key <> $val»;
$stfib .= «0»;
>elseif ((bccomp($st10, $val)) >= 0) echo «
$key <> $val»;
$stfib .= «1»;
$st10 = bcsub($st10, $val);
>
>
fg:<>
echo «
В СС на основе ряда Фибоначчи: «;
$stfib = ltrim ($stfib,’0′);
echo «$stfib»;
if ($st10 == 0) echo «
Фибоначчи сосчитано верно»;
>else echo «
Alarm $st10″;
>
>
?>
Как видно из кода, решением проблемы обработки длинных чисел здесь стало использование расширения PHP для длинной арифметики (функции bcadd, bccomp, bcdiv и др.). Поскольку для наглядности должен был выводиться весь используемый ряд Фибоначчи, а переводить требовалось всего 1 слово, вводимая строка была ограничена 12-ю символами, хотя данный способ позволяет обрабатывать и более длинные строки.
Передавалось слово на исполнение следующим способом:
action = «result.php»>
Введите фамилию:
name = «Surname»
value = «»>
Результат
Поскольку интересовал меня исключительно итог расчета в виде соответствующих чисел, дизайн соответствует принципам необходимости и достаточности:
Форма ввода 
Отказ при превышении длины 
Результат 
… 
Вывод
Возможно это тема старших классов школы или первых курсов университета, но мне довелось с ней столкнуться только сейчас. Впрочем, это оказалось весьма интересно. Надеюсь этот материал окажется полезным для вышеозначенной категории людей и не только. Спасибо за внимание.
С уважением, Sindoatan.
- PHP
- длинная арифметика
- системы счисления
- фибоначчи
Источник: habr.com