Алгоритм программы крестики нолики

Недавно я написал непобедимую игру «Крестики-Нолики». Это был интересный и поучительный проект, который многому меня научил. Если у вас есть желание посмотреть результат — это можно сделать здесь.

Для того чтобы сделать игру непобедимой, было необходимо создать алгоритм, который может рассчитать все возможные ходы для «компьютерного» игрока. Далее, нужно использовать некоторую метрику, чтобы определить, какой ход является предпочтительным. После долгих исследований стало понятно, что алгоритм Минимакс, был тем, что мне нужно.

Понимание основ алгоритма и реализация игры заняли некоторое время. Я нашел много примеров кода и объяснений, тем не менее это оказалось не такой уж простой затеей. Надеюсь этот пост поможет некоторым из читателей оценить элегантность этого алгоритма.

Описание «Идеальной» игры «Крестики-Нолики»

Для начала давайте опишем, что мы понимаем под «идеальной» игрой — если я играю идеально, я или побеждаю в игре, или играю вничью. В случае если я играю против другого «идеального» игрока, я всегда играю вничью.

Непобедимый соперник в игре крестики-нолики — решение задачи на Python

Можно ли описать эти требования количественно? Давайте для всех возможных вариантов конечного состояния игры назначить какое-то количество очков:

• Я победил, ура! Я получаю 10 очков!
• Я проиграл, блин. Я теряю 10 очков (потому, что другой игрок получает 10 очков).
• Ничья. Я получаю ноль, и другой игрок получает ноль.

Теперь мы можем количественно оценить любое конечное состояние игры.

Давайте рассмотрим короткий пример.

На картинке изображено состояние игрового поля, и мой черед ходить. Я играю за «Х». Моя цель, очевидно, максимизация количества очков, которые я получу.

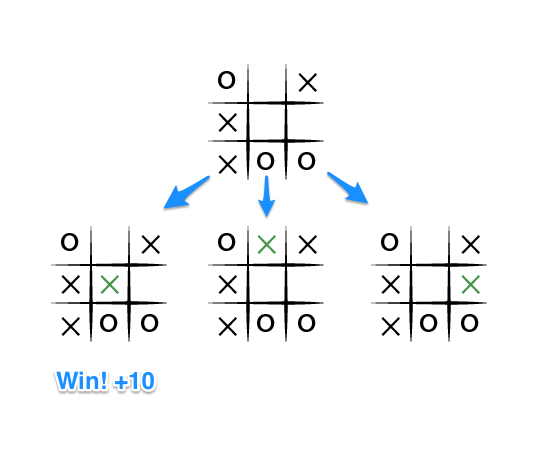
Верхняя часть картинки показывает состояние игры, и, в зависимости от моего выбора, я могу попасть в одно из трех состояний из нижней части картинки. Очевидно, что состояние, в котором я побеждаю (снизу слева) является наилучший. Если я не сделаю этот ход, игрок «О» может легко победить, и я не хочу, чтоб он победил. Таким образом, выберу ход, который принесет мне наибольшее число очков.

Но что мы знаем о втором игроке? Мы можем предположить, что он тоже играет с целью победить в игре. Игрок «О» хочет выбрать ход, который приведет к наименьшему выигрышу для нас, он хочет минимизировать наш выигрыш. Давайте посмотрим на вещи с точки зрения игрока «О» начиная с двух других состояний игры из предыдущего примера, тех, в которых я не побеждаю:

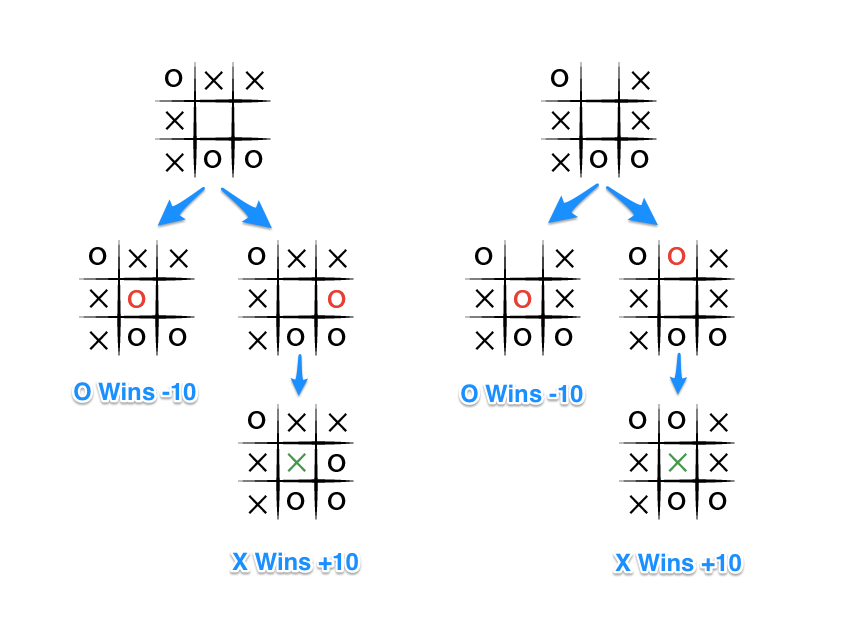
Выбор очевиден, «О» выберит один из ходов, который приведет нас к результату -10.

Описание алгоритма Минимакс

Суть алгоритма Минимакс это поочередный перебор возможных ходов двух игроков, при котором мы считаем, что игрок «чья очередь» выберет ход, приносящий максимальное количество очков. Предположим, что мы играем за игрока «Х», тогда описание алгоритма будет примерное таким:

Алгоритм «МиниМакс» в игре «Крестики-Нолики»

• Если игра закончена, вернуть количество очков для игрока «Х»
• В противном случае, получить список новых состояний игровой области для каждого возможного хода
• Оценить возможный выигрыш для каждого возможного состояния
• Для каждого из возможных состояний добавить «Минимакс» оценку текущего состояния
• Если ход игрока «Х» — вернуть ход с максимальным количеством очков
• Если ход игрока «О» — вернуть ход с минимальным количеством очков

Алгоритм является рекурсивным, и расчёт производится по очереди для каждого из игроков до тех пор, пока не рассчитан финальный выигрыш. Давайте посмотрим, как алгоритм работает с полным деревом ходов, и посмотрим, как будет выбран наилучший ход:

• В состоянии 1 — очередь ходить у игрока «Х». «Х» генерирует состояния 2, 3 и 4 и рекурсивно применяет алгоритм к сгенерированным состояниям
• Состояние 2 добавляет выигрыш в размере +10 к оценке состояния 1, потому что игра выиграна
• Состояния 3 и 4 не являются конечными состояниями, поэтому из состояния 3 генерируются состояния 5 и 6, из состояния 4 генерируются состояния 7 и 8, после чего к каждому из сгенерированных состояний применяется алгоритм Минимакс.
• Состояние 5 добавляет «проигрыш в размере -10 для состояния 3, то же самое происходит и с состоянием 7 для состояния 4.
• Состояния 6 и 8 генерируют лишь конечные выигрышные состояния, поэтому каждое из них добавляет выигрыш в размере +10 для состояний 3 и 4.
• Так как на состояниях 3 и 4 очередь ходить игрока „О“, „О“ будет искать наименьший выигрыш. Исходя из выбора в -10 и +10, оба состояния вернут -10
• Наконец, оценка выигрыша для состояний 2, 3 и 4 будет рассчитана как +10, -10 и -10 соответственно. Так как игрок „Х“ стремиться максимизировать выигрыш, будет сделан выбор в пользу состояния 2.

Как видите, здесь немалое количество вычислений, и именно поэтому нам нужен компьютер, чтоб применить этот алгоритм.

Реализация алгоритма Минимакс

Надеюсь теперь у вас есть общее представление, как алгоритм Минимакс определяет наилучший ход. Давайте рассмотрим имплементацию алгоритма, чтоб закрепить наше понимание.
Вот функция, которая производит оценку состояния:

Достаточно просто, вернуть +10 если текущий игрок побеждает в игре, -10, если проигрывает и 0 в случае ничьи. Вы также можете отметить, что с точки зрения алгоритма нет разницы, какой это игрок («Х» или «О»), важно лишь чей ход.

А теперь собственно сам алгоритм; обратите внимания что в приведенном варианте выбор хода это просто адрес ячейки на поле, т.е. [0,2] это правая верхняя ячейка на игровом поле размером 3×3.

Когда алгоритм выполняется в классе PerfectPlayer, выбор наилучшего ходя сохраняется в переменной choice, которая впоследствии используется для того, чтобы вернуть новое состояние игры в которое мы попадаем в результате выбранного игроком хода.

Идеальный игрок-самоубийца

Эта имплементация алгоритма позволит вам создать игру в «крестики-нолики», в которую вы не сможете победить. Но есть маленький нюанс, который я обнаружил в процессе тестирования игры. В случае, если мой «идеальный игрок» обнаружит состояние, в котором он или проиграет, или закончит вничью, его ход будет самоубийственным. Проще говоря, алгоритм говорит «я все равно проиграю, поэтому без разницы сейчас, или через 6 ходов».

Я обнаружил это когда передал явно некорректное состояние игрового поля и попытался выяснить, какой ход предложит алгоритм. Я ожидал, что «идеальный игрок» попытается помешать мне выиграть так долго, как сможет, но этого не произошло:

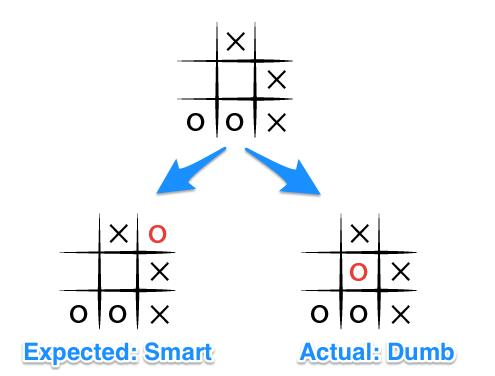
Давайте рассмотрим, что происходит здесь через призму возможных ходов (для простоты я удалил некоторые состояния)

• В случае если игровое поле в состоянии 1, и оба игрока играют идеально, и компьютер играет на стороне „О“, „О“ принимает решение идти в состояние 5, что ведет к немедленному проигрышу, когда игрок „Х“ переходит в состояние 9.
• Но если „О“ заблокирует ход „Х“ перейдя в состояние 3, „Х“ заблокирует потенциально победный ход „О“, как показано в состоянии 7.
• Исходя из этого очевидно, что „Х“ победит, как показано в состояниях 10 и 11, несмотря на то, какой ход выберет „О“.

В результате данных расчетов, принимая во внимание факт, что при расчёте выигрыша мы итерируемся слева направо, снизу вверх, не проводя различий между ходами, будет выбран ход, приводящий в состояние 5, так как это последний доступный ход из состояния 1.

Черт побери, что же мастер «крестиков-ноликов» должен сделать?

Даем противнику хороший бой: глубина

Наилучшим улучшением для алгоритма будет изменить его так, чтоб «идеальный игрок» играл «идеально» до самого конца, т.е. взять «глубину» (количество ходов до возможного проигрыша) в расчет при выборе хода. Простыми словами, идеальный игрок будет играть идеально, и постарается играть так долго, как только сможет.

Для того чтобы достигнуть такого результата мы будем отнимать глубину рекурсииколичество ходов от конечного состояния игры. Т.е. чем больше ходов до минимального выигрыша (и чем меньше ходов до максимального) — тем лучше.

Так, каждый раз при вызове алгоритма Минимакс глубина будет увеличена на 1, и когда мы наконец рассчитаем возможный выигрыш для конкретного конечного состояния игры мы введем поправку на глубину. Давайте посмотрим, как это выглядит на примере следующего дерева ходов:

Теперь учет глубины (как показано черным слева) приводит к тому, что оценка различается для каждого конечного состояния, и, потому что на первом уровне Минимакс будет пытаться максимизировать возможный выигрыш (т.к. ход игрока «О») предпочтительная оценка выигрыша составит -6, т.к. это выше чем альтернативный вариант в -8. И потому, несмотря на то, что игроку грозит верная смерть, наш надежный «идеальный игрок» выберет ход, который приведет к достойной смерти, и заблокирует выигрыш игрока «Х».

Источник: temofeev.ru

Крестики-нолики — создание непревзойденного ИИ

В сегодняшней статье я покажу вам, как создать непревзойденного ИИ-агента, играющего в классическую игру Крестики-Нолики. Вы познакомитесь с концепцией алгоритма Minimax, который широко и успешно используется в таких областях, как Искусственный интеллект, Экономика, Теория игр. , Статистика или даже Философия.

Оглавление

• Про крестики-нолики
• Минимаксный алгоритм
• Непревзойденный ИИ в крестиках-ноликах
• Бонус
• «Что дальше?»

Прежде чем мы перейдем к части ИИ, давайте удостоверимся, что мы понимаем игру.

О крестиках-ноликах

Крестики-нолики (также известные как крестики-нолики или крестики-нолики) — это игра с карандашом и бумагой для двоих. игроки X и O, которые по очереди отмечают поля в сетке 3 × 3. Игрок, которому удастся разместить три своих метки в горизонтальном, вертикальном или диагональном ряду, выигрывает игру.

Я рекомендую вам поиграть в игру самостоятельно, не стесняйтесь проверить мое приложение Крестики-нолики для iOS.

Чтобы решить крестики-нолики, нам нужно пойти глубже, чем просто думать об этом как об игре, в которой два игрока ставят крестики и нолики на доске. Формально Tic Tac Toe — это игра с нулевой суммой и точной информацией. Это означает, что выигрыш каждого участника равен проигрышу других участников, и мы знаем все о текущем состоянии игры.

В игре с двумя игроками (A против B), если игрок A набирает x очков (вспомогательные единицы), игрок B теряет x очков. Общая сумма прибылей / убытков всегда равна 0.

Имея это в виду, давайте перейдем к алгоритму Minimax, который подходит для таких случаев.

Минимаксный алгоритм

Minimax — это рекурсивный алгоритм, который используется для выбора оптимального хода для игрока, предполагая, что противник также играет оптимально. Как следует из названия, его цель — минимизировать максимальные потери (минимизировать наихудший сценарий).

Вы можете думать об алгоритме как о представлении процесса мышления человека, когда он говорит: «Хорошо, если я сделаю этот ход, то мой противник сможет сделать только два хода, и каждый из них позволит мне выиграть. Так что это правильный шаг ».

Посмотрим на код!

Строка 1

Чтобы вычислить минимаксный счет, давайте скармливаем функции минимакса текущее состояние доски ([Player]) и игрока-оппонента (Player).

Строки 2–4

Тогда давайте проверим, есть ли на доске победитель. Если в функцию был передан проигрыватель, мы возвращаем 1, иначе -1.

Строки 9–19

После этого давайте попробуем каждый возможный ход и рекурсивно вычислим для него минимаксный счет.

Если минимаксная функция не находит конечное состояние, она продолжает рекурсивно идти уровень за уровнем глубже в игру. Эта рекурсия происходит до тех пор, пока она не достигнет конечного состояния и не вернет результат на один уровень выше.

Строки 20–23

Если счет был обновлен, мы возвращаем его как минимаксный счет; в противном случае — ничья, поэтому мы возвращаем 0.

Я знаю. Поначалу это может показаться пугающим и не интуитивным. В основном из-за его рекурсивной природы, но как только вы увидите его в действии, вы легко поймете это.

Без лишних слов, давайте перейдем к примеру, чтобы лучше понять, что происходит.

Непревзойденный искусственный интеллект Tic Tac Toe

Давайте посмотрим на следующее состояние доски. Мы постараемся решить его как X.

Как бы вы ее решили?

Думаю, вы могли бы подумать, что лучшим ходом в таком сценарии было бы поставить X в центр доски и выиграть игру.

И вы были бы правы, но разве это единственное выигрышное решение для X? Как получить это решение?

Чтобы определить это, нарисуем дерево всех возможных состояний доски.

Как видно выше, начиная с начального состояния 0.0, у нас есть 3 возможности (1.0, 1.1, 1.2).

1.0 дает нам победу (+1), но давайте рассмотрим и другие пути.

1.1 дает нашему оппоненту 2 возможности (2.0, 2.1). 2.0 — это выигрышное состояние для нашего оппонента, поэтому это проигрышное состояние для нас (-1). 2.1 дает только одну возможность 3.0, в которой мы выигрываем (+1).

1.2 дает нашему оппоненту 2 возможности (2.2, 2.3). 2.2 — это выигрышное состояние для нашего оппонента, поэтому это проигрышное состояние для нас (-1). 2.3 дает только одну возможность 3.1, в которой мы выигрываем (+1).

Хорошо, но как мы можем это интерпретировать?

Давайте начнем с конечных состояний внизу и вычислим минимаксные оценки.

На глубине 3 мы максимизируем, поэтому мы распространяем оценку +1 на предыдущие ходы на глубине 2 .

На глубине 2 мы минимизируем, поэтому мы распространяем -1 баллы на предыдущие ходы на глубине 1. .

На глубине 1 мы максимизируем, поэтому мы распространяем +1 на предыдущее движение на глубине 0.

В конечном итоге на глубине 0, где мы на самом деле находимся, мы должны выбрать ход, связанный с полученным результатом +1.

Tic Tac Toe AI решит перейти к узлу 1.0 и выиграть игру.

Наш Tic Tac Toe AI симулирует каждое движение, что делает себя непобедимым противником.

Но что делает его непобедимым?

Из-за относительно небольшого пространства состояний (3⁹ = 196839 возможных комбинаций досок) он может легко искать оптимальное решение во всем дереве игры, рассматривая игру как полностью детерминированную среду.

С другой стороны, шахматы, например, имеют чрезвычайно большое пространство состояний ~ 10¹²⁰ возможностей.

С такими обширными пространствами поиска мы все еще можем использовать алгоритм Minimax, но мы должны помнить об ограничении глубины нашего поиска. В противном случае мы можем рассчитывать результаты очень долго или даже навсегда.

Короче говоря, чем меньше пространство состояний, тем лучших результатов мы можем достичь с помощью алгоритма Minimax.

tl; dr Tic Tac Toe AI непревзойден. Вы можете рисовать самое большее и только при совершенной игре. Если вы думаете, что можете перехитрить его и выиграть игру, дайте мне знать, как это сделать, в разделе комментариев.

Бонус

Если вам интересно узнать о других играх, основанных на крестиках-ноликах, не сомневайтесь, попробуйте Ачи и Скалы! Эти расширения Tic Tac Toe намного сложнее, чем оригинальная версия, и требуют более продвинутых стратегий!

Что дальше?

К настоящему времени вы должны быть в состоянии понять принципы, лежащие в основе алгоритма Minimax, который позволил нам создать непревзойденного агента Tic Tac Toe AI. Minimax — очень мощный и универсальный алгоритм, который можно применять в самых разных приложениях. Не стесняйтесь применять его к другим задачам принятия решений. Жду ваших результатов!

Не забудьте проверить приложение проекта для iOS.

Вопросов? Комментарии? Не стесняйтесь оставлять свои отзывы в разделе комментариев или связываться со мной напрямую по адресу https://gsurma.github.io.

И не забудьте если вам понравилась эта статья .

Источник: digitrain.ru

Алгоритм крестиков-ноликов

В последнее время преподаватели многих вузов начали давать своим студентам задание разработать программу, играющую в крестики-нолики. Несмотря на видимую простоту, это не совсем тривиальная задача. Поэтому я начал получать большое количество писем с просьбой о помощи. Постепенно я пришел к выводу, что необходимо сделать алгоритм этой игрушки общедоступным.

У меня есть только одна просьба к тем, кто будет пользоваться плодами моего труда: если вы отнеслись к процессу творчески и внесли в алгоритм существенные изменения или разработали свой алгоритм, пожалуйста, сообщите мне об этом — мне это интересно.

Все примеры приведены на Паскале. Определим основные массивы, с которыми будем работать:

type position=array [1..9] of byte; var Kl : position; Ray: position;

Здесь Kl — клетки поля. Принимаемые значения:

0 — для пустой клетки;

1 — для крестика;

Ray — рейтинги клеток. Вычисляются для каждой позиции из массива Kl. Опираясь на рейтинги, компьютер принимает решение о предпочтительности хода на то или иное поле. Собственно,алгоритм вычисления массива Ray и есть главная часть алгоритма крестиков-ноликов. Если известен массив Ray, то выбрать клетку для хода уже легко. Например, так:

procedure SelectCell; var m,r,mr,i: byte; begin ch:=false; m:=0;r:=0; if lvl=0 then begin for i:=1 to 9 do r:=r+Ray[i]; mr:=random(r)+1; for i:=1 to 9 do begin mr:=mr-Ray[i]; if mrr then r:=Ray[i]; for i:=1 to 9 do if Ray[i]=r then m:=m+1; mr:=random(m)+1; m:=0; for i:=1 to 9 do begin if Ray[i]=r then begin m:=m+1; if m=mr then begin Kl[i]:=4; DrawCell(i); break end end end end end;

Здесь реализовано два алгоритма выбора клетки для хода в зависимости от глобальной переменной lvl, определяющей уровень игры компьютера. При lvl=0 вероятность хода на данную клетку пропорциональна ее рейтингу, т.е. компьютер с малой вероятностью, но все же может сходить на клетку с низким рейтингом. При ином значении переменной lvl компьютер ходит только на клетку с максимальным рейтингом, а если таких клеток несколько, то среди них нужная клетка выбирается случайно. Естественно, вторая стратегия при правильном определении массива Ray задает более высокий уровень игры компьютера.

Глобальная переменная ch: boolean служит для разрешения/запрещения хода человеком. Не описанная здесь процедура DrawCell(i:byte) перерисовывает нужную клетку на экране монитора.

Другая важная процедура — это функция, определяющая, закончилась игра после данного хода или нет. Эта функция вызывается как после хода человека (до вычисления рейтингов), так и после хода компьютера. Функция анализирует все значащие ряды, т.е. горизонтали, вертикали и диагонали и, если на одном из них оказывается три одинаковых фигуры, то присваивает победу нужной стороне. Если же на всех рядах присутствуют как крестики, так и нолики, то выдается ничейное значение. Если ни одно из этих условий не выполнено, то игра считается неоконченной — выдается ноль. Для анализа рядов функция пользуется массивом-константой lin, который определяется следующим образом:

const lin : array[1..8,1..3] of byte = ((1,2,3),(4,5,6),(7,8,9), (1,4,7),(2,5,8),(3,6,9), (1,5,9),(3,5,7));

Вот эта функция:

function Fin(pos: position) var ni,sa,so,i,j,sj,res:byte; begin ni:=5; res:=0; for i:=1 to 8 do begin sa:=5;so:=0;li[i]:=0; for j:=1 to 3 do begin sj:=pos[lin[i,j]]; sa := sa and sj; so := so or sj; li[i] := li[i] + sj end; res := res or sa; ni := ni and so end; if ni=5 then res:=3; Fin:=res end;

Видно, что выходными значениями этой функции являются:

1 — победа крестиков;

4 — победа ноликов;

0 — игра не окончена.

Глобальный массив li: array [1..8] of byte для определения признаков окончания игры не нужен. В нем предварительно готовятся данные (суммы значений фигур по каждому ряду) для дальнейшего определения рейтингов полей.

Анализ ситуации на поле производится после каждого полухода ( т.е. хода человека или компьютера) следующим образом:

procedure Analis; begin case Fin(Kl) of 0 : if ch then Rayting; 1 : StopGame(«Вы выиграли»); 3 : StopGame(«Ничья»); 4 : StopGame(«Вы проиграли»); end end;

Здесь StopGame — процедура, блокирующая продолжение игры с выводом соответствующего сообщения (подробно здесь не описывается). Процедура Rayting и есть главная подпрограмма, определяющая предпочтительность того или иного хода для компьютера.

От ее реализации во многом зависит характер игры компьютера. Ясно, что наивысший рейтинг должен присваиваться полям, ход на которые ведет к немедленному выигрышу (мы дадим им значение 1000000). Следующие по важности — это поля, ход на которые способен предотвратить немедленный проигрыш (рейтинг 100000).

Если указанных полей нет, то становятся важными поля, после хода на которые выигрыш неизбежен на следующем ходу (т.е. противнику ставится вилка — рейтинг 10000). Затем идут ходы, способные предотвратить вилку противника (1000). Более низкие рейтинги имеют подготовка вилки (100) и предотвращение подготовки вилки противником (10). И, наконец, просто пустая клетка, ход на которую возможен, имеет рейтинг 1 (в отличие от занятой клетки, рейтинг которой 0).

Для реализации процедуры, присваивающей рейтинги по вышеизложенному принципу, нам понадопится еще один вспомогательный массив-константа:

const kle : array [1..9,1..4] of byte = ((1,4,7,0),(1,5,0,0),(1,6,0,8), (2,4,0,0),(2,5,7,8),(2,6,0,0), (3,4,0,8),(3,5,0,0),(3,6,7,0));

Из этого массива легко определить номера рядов, в которые входит данная клетка, т.е. массив выполняет роль, обратную по сравнению с массивом lin.

Сама процедура Rayting имеет вид:

procedure Rayting; var s00,s11,s44: array [0..3] of byte; s0,s1,s4,ssj,ii,j,jj,jjj,sj: byte; begin for ii:=1 to 9 do Ray[ii]:=0; for ii:=1 to 9 do if Kl[ii]=0 then begin Ray[ii]:=Ray[ii]+1; s0:=0;s1:=0;s4:=0; for j:=1 to 4 do begin ssj:=kle[ii,j]; if ssj<>0 then case li[ssj] of 0 : begin s00[s0]:=ssj; inc(s0); for jj:=0 to s4-1 do for jjj:=1 to 3 do begin sj:=lin[ssj,jjj]; if sj<>ii then Ray[sj]:=Ray[sj]+100 end for jj:=0 to s1-1 do begin for jjj:=1 to 3 do begin sj:=lin[ssj,jjj]; Ray[sj]:=Ray[sj]+10; end for jjj:=1 to 3 do begin sj:=lin[s11[jj],jjj]; if (sj<>ii)and(Kl[sj]=0) then Ray[sj]:=Ray[sj]+10 end end end; 1 : begin s11[s1]:=ssj; inc(s1); if s1>1 then begin Ray[ii]:=Ray[ii]+1000; for jj:=0 to s1-1 do for jjj:=1 to 3 do begin sj:=lin[s11[jj],jjj]; if (sj<>ii)and(Kl[sj]=0) then Ray[sj]:=Ray[sj]+1000 end end; for jj:=0 to s0-1 do begin for jjj:=1 to 3 do begin sj=lin[ssj,jjj]; if Kl[sj]=0 then Ray[sj]:=Ray[sj]+10 end; for jjj:=1 to 3 do begin sj:=lin[s00[jj],jjj]; if (sj<>ii)and(Kl[sj]=0) then Ray[sj]:=Ray[sj]+10 end end end; 2 : Ray[ii]:=Ray[ii]+100000 4 : begin s44[s4]:=ssj; inc(s4); if s4>1 then Ray[ii]:=Ray[ii]+10000; for jj:=0 to s0-1 do for jjj:=1 to 3 do begin sj:=lin[s00[jj],jjj]; if sj<>ii then Ray[sj]:=Ray[sj]+100 end end; 5 : ; 8 : Ray[ii]:=Ray[ii]+1000000; end end end end;

Процедура Rayting позволяет реализовать достаточно сильную игру компьютера, причем «рассуждения» компьютера в данном случае близки к логике человека.

Кроме того, несмотря на некоторую громоздкость алгоритма, процедура выполняется достаточно быстро, что позволяет ее использовать на слабых компьютерах или при реализации на интерпретируемых языках программирования. Так, я применил этот алгоритм для Flash-варианта крестиков-ноликов. Недостатком можно считать некоторое однообразие игры (отбрасывание некоторых вполне приемлемых вариантов хода, особенно в самом начале игры). Алгоритм вполне может быть улучшен, однако это я оставляю на усмотрение других разработчиков.

В программе, написанной на Delphi, применен другой вариант процедуры Rayting:

procedure Rayting; var i: byte; begin for i:=1 to 9 do if Kl[i]=0 then Ray[i]:=NextStep(Kl,i,4,0) else Ray[i]:=0 end;

Здесь NextStep(pos:position;i,fig,wlo:byte):byte — рекурсивная функция, позволяющая для данной позиции pos оценить рейтинг хода на клетку i фигурой fig при глубине данного хода wlo (в полуходах). Она имеет вид:

function NextStep(pos:position;i,fig,wlo:byte):byte; var j : byte; ra:position; begin pos[i]:=fig; inc(wlo); if fig=1 then fig:=4 else fig:=1; Result:=Fin(pos) shl 3; if Result<>0 then exit; if wlo24 then dec(ra[j]) end; if fig=1 then begin Result:=32; for j:=1 to 9 do if (pos[j]=0) and (Result>ra[j]) then Result:=ra[j] end else begin Result:=8; for j:=1 to 9 do if (pos[j]=0) and (Result < ra[j]) then Result:=ra[j] end end else Result:=16 end;

Максимальная глубина расчета задается глобальной переменной glub, что позволяет изменять уровень игры компьютера, изменяя эту переменную, а не переменную lvl.

То есть, в процедуре SelectCell можно оставить только вторую половину кода. Кроме того, в этом случае не используются массивы li и kle. К сожалению, данный алгоритм работает медленнее, и его применение, например, в варианте Macromedia Flash очень сильно замедляет работу программы. Однако, при составлении программы на языках, использующих достаточно эффективный компилятор (Pascal, Delphi, C) алгоритм дает очень хорошие результаты.

Процедура Rayting при этом присваивает рейтинги полям по следующей шкале: 25..32 — ходы, приводящие к выигрышу ноликов, причем 32 соответствует немедленному выигрышу, 31 — выигрышу через полуход, 30 — через 2 полухода и т.д.; 24 — ходы, приводящие к гарантированной ничьей; 16 — ходы с непредсказанным результатом (т.е. глубина расчета, заданная переменной glub, оказалась недостаточной, чтобы судить о последствиях данного хода); 8..15 — поля, ход на которые при правильных ходах противника ведет к проигрышу, причем 8 — немедленный проигрыш, 9 — проигрыш через полуход, 10 — через два полухода и т.д.

Этот вариант расчета рейтингов слабо (практически, только через процедуру Fin) связан с особенностями крестиков-ноликов и может быть применен для любой другой пошаговой позиционной игры вплоть до шахмат, если, конечно, скорости компьютера хватит для оценки всех возможных вариантов ходов на нужную глубину.

Можно предложить и другие варианты расчета рейтинга. Так, например, можно просто составить таблицу, переводящую все возможные варианты массива Kl в массив Ray. Несмотря на громоздкость такой таблицы и большую трудоемкость ее составления, такой метод может оказаться наиболее быстродействующим. Кроме того, изменение этой таблицы сразу меняет характер игры компьютера.

Наиболее интересен вариант с таблицей, когда она хранится в отдельном файле и программа корректирует ее в зависимости от результатов предыдущих игр — так называемый самообучаемый алгоритм. В этом случае первоначальный вид таблицы может быть очень простым: компьютер сам приведет ее к оптимальному виду в процессе обучения.

Источник: beluch.ru