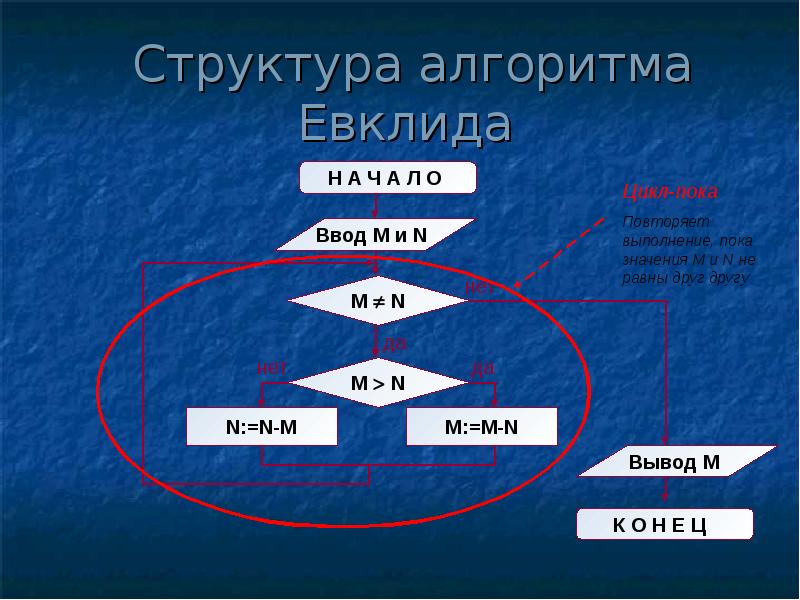
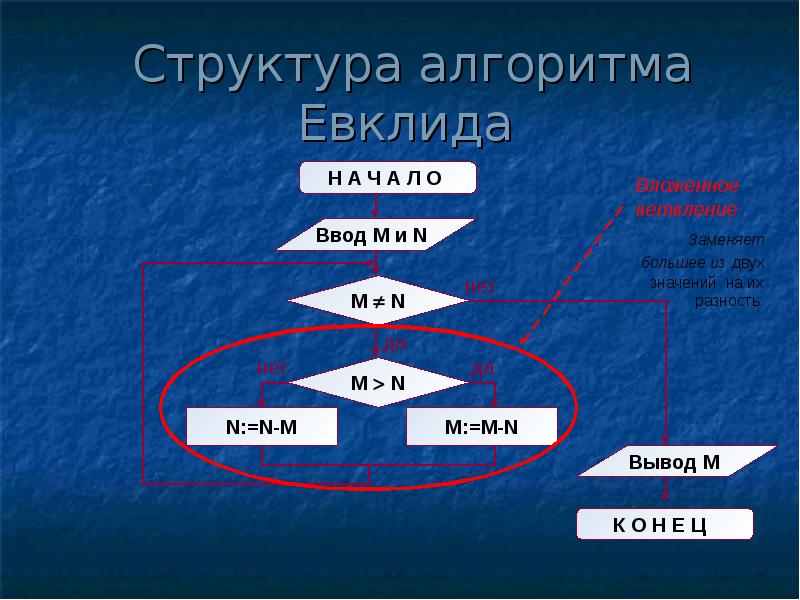
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
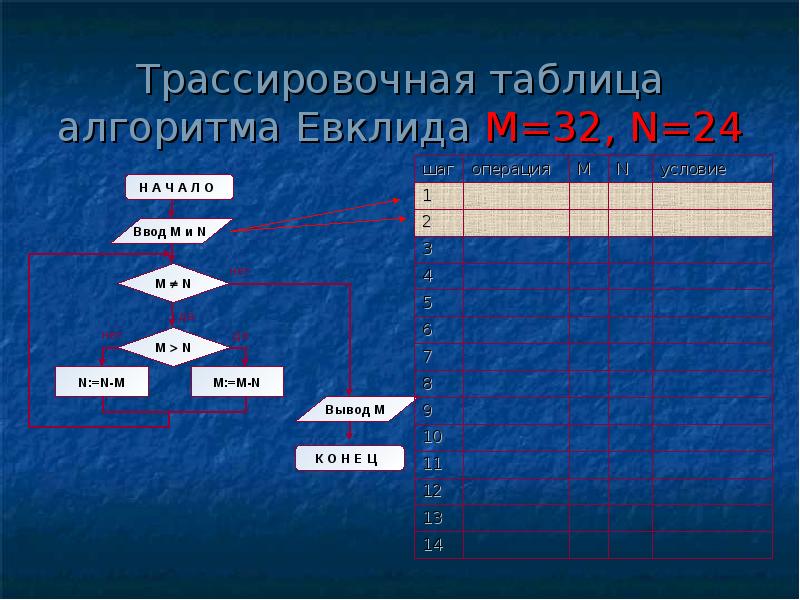
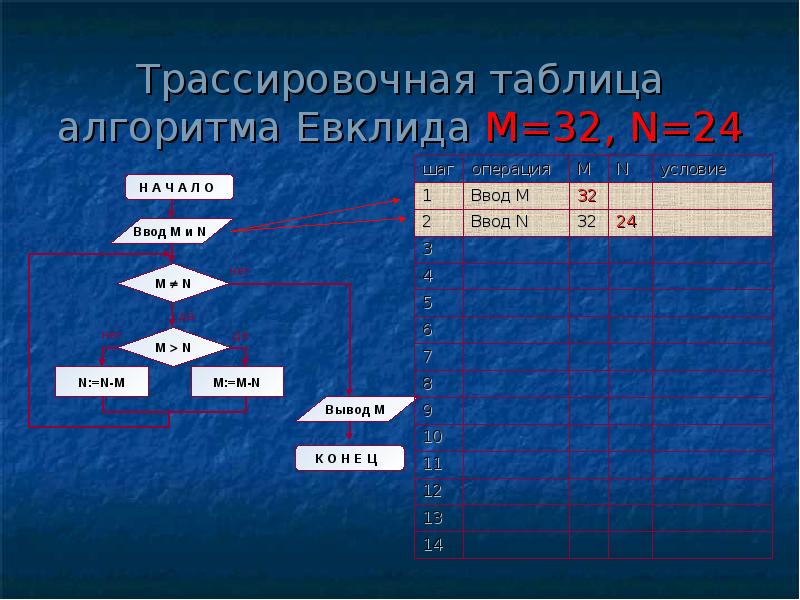
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24.
| Шаг | Операция | M | N | Условие |
| ввод М | ||||
| ввод N | ||||
| M ¹ N | 32 ¹ 24, да | |||
| M>N | 32>24, да | |||
| M:=M-N | ||||
| M ¹ N | 8 ¹ 24, да | |||
| M>N | 8>24, нет | |||
| N:=N-M | ||||
| M ¹ N | 8 ¹ 16, да | |||
| M>N | 8>16, нет | |||
| N:=N-M | ||||
| M ¹ N | 8 ¹ 8, нет | |||
| вывод M | ||||
| конец |
В итоге получился верный результат.
Программа на АЯ и на Паскале
Запишем алгоритм на АЯ и программу на Паскале.
Уроки Pascal. НОД (наибольший общий делитель)
| алг Евклид цел М, N нач вывод » Введите М и N» ввод М, N пока М N, повторять нц если M>N то M:=M-N иначеN:=N-M кв кц вывод «НОД=»,М кон | Program Evklid; var M, N: integer; begin writeln(‘Введите М и N’); readln(M, N); while M<>N do begin if M>N then M:=M-N else N:=N-M end; write(‘Н0Д=’,М) end. |
Вопросы и задания
1. Выполните на компьютере программу Evklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
НОД(А, B, С) = НОД(НОД(А, В), С).
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
А × В = НОД(А, В) × НОК(А, В).
Таблицы и массивы
Изучая базы данных, электронные таблицы, вы познакомились с табличным способом организации данных. Вы уже знаете, что большие наборы данных удобно представлять в табличном виде. В таблицах могут храниться данные разных типов. На практике чаще всего приходится встречаться с таблицами, содержащими числовые и символьные (текстовые) данные.
Что такое массив
Представление таблицы в языках программирования называется массивом. Вот, например, таблица, содержащая среднемесячные значения температуры в Перми в 2000 году:
| Месяц | ||||||||
| Температура | -21 | -18 | -7,5 | 5,6 | 22,2 | 5,4 | -7 | -18 |
Такую таблицу называют линейной. Она представляет собой последовательность упорядоченных чисел. Для обозначения этих чисел используют индексированные имена. Например, через Т[1] обозначается температура в январе (первом месяце года), Т[5] — температура в мае и т. д.
В программировании линейная таблица называется одномерным массивом. В нашем примере Т — это имя массива. Элементы массива пронумерованы. Порядковый номер элемента называется его индексом. Каждый элемент массива обозначается индексированным именем в следующей форме:
Программирование разветвляющихся алгоритмов
Индекс записывается в квадратных скобках: Т[2], Т[10], Т[12]. Индексы могут представляться не только в виде констант, но и в виде целых переменных и даже выражений целого типа: T[i], T[k], T[i+k], T[2*k]. Важно следить, чтобы значения индексов не выходили за допустимые границы. В примере с температурами они должны лежать в диапазоне от 1 до 12.
Все элементы массива должны иметь одинаковый тип. Если массив состоит только из целых чисел, то тип массива — целый. В нашем примере значения температур могут быть дробными, поэтому тип массива — вещественный.
Массив — это пронумерованная конечная последовательность однотипных величин.
Решение задач по обработке массива связано, как правило, с перебором элементов массива. Такой перебор происходит в цикле, в котором изменяется значение индекса от начальной до конечной величины. Для того чтобы организовать ввод исходных данных в массив, нужно также использовать цикл.
Описание и ввод значений в массив на Алгоритмическом языке
Запишем алгоритм ввода значений в массив температур. Сначала посмотрим, как это делается на АЯ. Рассмотрим два варианта алгоритмов на АЯ, использующих разные способы организации цикла.
алг Ввод массива, вариант 1
вещ таб Т[1:12]
цел I
нач I:=1
пока Iповторять
нц
вывод («Т[,» I, «]=»)
ввод (Т[I])
I:=I+1
кц
кон
алг Ввод массива, вариант 2
вещ таб Т[1:12]
цел I
нач
для I от 1 до 12 шаг 1 повторять
нц
вывод («Т[«,I,»]= «)
ввод (Т[I])
кц
кон
Обратите внимание на вторую строку алгоритмов. В ней присутствует описание массива температур. В Алгоритмическом языке массив называется таблицей. Запись
вещ таб Т[1:12]
описывает таблицу (массив) вещественного типа, имя которого Т и элементы пронумерованы от 1 до 12.
Цикл с параметром в АЯ
В первом варианте алгоритма используется уже знакомая вам алгоритмическая структура цикла с предусловием. Переменная I играет роль параметра цикла, изменяющегося от 1 до 12 с шагом 1. Внутри цикла она используется в качестве индекса в обозначении элементов цикла: Т[I].
Ввод организован в режиме диалога. Вы уже знаете, что это обязательное условие дружественности интерфейса программы. Перед вводом каждого очередного элемента таблицы на экран будет выводиться его имя. Это результат выполнения команды вывод «Т[«, I, «]=». После этого программист должен ввести с клавиатуры соответствующее число (команда ввод Т[I]):
Во втором варианте используется алгоритмическая структура, которая называется «цикл с параметром». Ее общая форма такая:
для от до шаг повторять
нц
кц
Параметром цикла должна быть переменная целого типа. В нашем примере это переменная I. Выполнение тела цикла повторяется для всех последовательных значений параметра от начального до конечного значения включительно с изменением его значения при каждом повторении на величину шага. Следовательно, по второму варианту алгоритма будут выполняться те же самые действия, что и по первому.


Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник: zdamsam.ru
Уроки 42 — 45
Циклы на языке Паскаль
(§ 15. Программирование циклов)
Разработка программ c использованием цикла с предусловием
Проследим все этапы технологии решения задачи на компьютере на примере конкретной задачи.

1. Постановка задачи. Дано N кубиков, на которых написаны разные буквы. Сколько различных N-буквенных слов можно составить из этих кубиков (слова не обязательно должны иметь смысл)?
Искомую целочисленную величину обозначим буквой F. Тогда постановка задачи выглядит так:

2. Математическая формализация. Получим расчетную формулу. Сначала рассмотрим несколько конкретных примеров. Имеются два кубика с буквами «И» и «К». Ясно, что из них можно составить два слова:
ИК КИ
Добавим к ним третью букву, «С». Теперь число разных слов будет в три раза больше предыдущего, т. е. равно 6:
ИКС КИС ИСК КСИ СКИ СИК
Если добавить четвертую букву, например «А», то число слов возрастет в четыре раза и станет равным 24:
КИСА КИАС КСИА КСАИ КАИС КАСИ ИКСА ИКАС ИСКА ИСАК ИАКС ИАСК СКИА СКАИ СИКА СИАК САКИ САИК АКИС АКСИ АИКС АИСК АСКИ АСИК.
Попробуйте записать все варианты слов из пяти букв: И, К, С, А, У. Сделать это непросто. Ясно лишь, что количество таких слов будет в пять раз больше 24, т. е. равно 120. Из шести букв можно составить 720 различных слов. С ростом числа букв число слов быстро растет.
Например, для 10 букв получается 3 628 800 слов.
Подобные задачи решает раздел математики, который называется комбинаторикой.
Количество различных комбинаций из N предметов, получаемых изменением их порядка, называется числом перестановок. Это число выражается функцией от N, которая называется факториалом и записывается так:
Читается: «эн факториал». Для любого натурального N значение N! вычисляется как произведение последовательности натуральных чисел от 1 до N. Например:
1! = 1; 2! = 1*2 = 2; 3! = 1*2*3 = 6; 4! = 1*2*3*4 = 24; 5! = 1*2*3*4*5 = 120 и т. д.
Теперь вернемся к формулировке задачи. Если N обозначает количество букв, а F — количество слов из этих букв, то расчетная формула такова:

3. Построение алгоритма. Поскольку алгоритм должен быть независимым от данного значения N, то его нельзя сделать линейным. Дело в том, что для разных N надо выполнить разное число умножений. В таком случае с изменением N линейная программа должна была бы менять длину.
Алгоритм решения данной задачи будет циклическим. С циклическими алгоритмами вы уже познакомились, работая с графическим исполнителем.

Цикл — это команда исполнителю многократно повторить указанную последовательность команд.
Рассмотрим блок-схему на рис. 2.7 и алгоритм на АЯ.
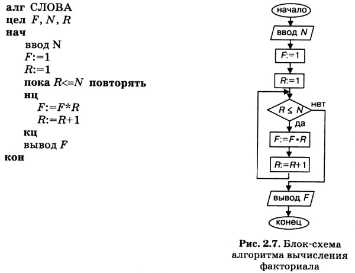
Здесь применена знакомая вам алгоритмическая структура «цикл с предусловием». Выполняется она так: пока истинно условие цикла, повторяется выполнение тела цикла.
Тело цикла составляют две команды присваивания, заключенные между служебными словами нц и кц. Условие цикла — это отношение R
В данном алгоритме переменная R выполняет роль множителя, значение которого меняется от 1 до N через единицу. Произведение накапливается в переменной F, начальное значение которой равно 1. Цикл заканчивается, когда R становится равным N + 1. Это значение в произведение уже не попадет.
Для проверки правильности алгоритма построим трассировочную таблицу (для случая N = 3):
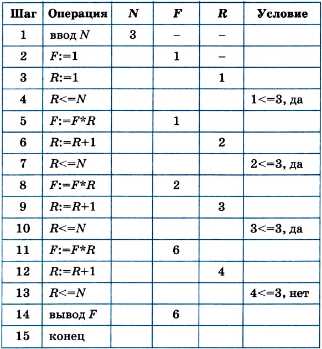
Из этой таблицы хорошо видно, как менялись значения переменных. Новое значение, присвоенное переменной, стирает ее старое значение (в данной таблице не повторяется запись значения переменной, если оно не изменяется; в таком виде таблица менее загромождена числами). Последнее значение F равно 6. Оно выводится в качестве результата. Очевидно, что результат верный: 3! = 6.

4. Составление программы. Чтобы составить программу решения нашей задачи, нужно научиться программировать циклы на Паскале. Основной циклической структурой является цикл с предусловием (цикл-пока). С помощью этой структуры можно построить любой циклический алгоритм. Оператор цикла с предусловием в Паскале имеет следующий формат:
while do
Служебное слово while означает «пока», do — «делать», «выполнять».
Оператор, стоящий после слова do, называется телом цикла. Тело цикла может быть простым или составным оператором, т. е. последовательностью операторов между служебными словами begin и end.
А теперь запрограммируем на Паскале алгоритм решения нашей задачи (добавив к нему организацию диалога).

Снова бросается в глаза схожесть алгоритма на АЯ и программы на Паскале. Обратите внимание на то, что в Паскале нет специальных служебных слов для обозначения конца цикла (так же как и конца ветвления). Во всех случаях, где это необходимо, используются слова begin и end.
Что такое отладка и тестирование программы

5. Отладка и тестирование. Под отладкой программы понимается процесс испытания работы программы и исправления обнаруженных при этом ошибок. Обнаружить ошибки, связанные с нарушением правил записи программы на Паскале (синтаксические и семантические ошибки), помогает используемая система програм- жирования. Пользователь получает сообщение об ошибке, исправляет ее и снова повторяет попытку исполнить программу.
Поиск алгоритмических ошибок в программе производится с помощью тестирования.

Тест — это конкретный вариант значений исходных данных, для которого известен ожидаемый результат. Прохождение теста — необходимое условие правильности программы. На тестах проверяется правильность реализации программой запланированного сценария.
Нашу программу, например, можно протестировать на значении N = 6. На экране должно получиться:
Введите число букв: 6
Из 6 букв можно составить 720 слов.

6. Проведение расчетов и анализ полученных результатов — этот этап технологической цепочки реализуется при разработке практически полезных (не учебных) программ. Например, программы «Расчет прогноза погоды». Ясно, что ею будут пользоваться длительное время, и правильность ее работы очень важна для практики. А поэтому в процессе эксплуатации эта программа может дорабатываться и совершенствоваться.
Коротко о главном
Последовательность этапов работы программиста при решении задачи на компьютере называется технологией решения задачи на компьютере.
Таких этапов шесть:
1) постановка задачи;
2) математическая формализация;
3) построение алгоритма;
4) составление программы на языке программирования;
5) отладка и тестирование программы;
6) проведение расчетов и анализ полученных результатов.
Количество различных комбинаций из N предметов, получаемых изменением их порядка, называется числом перестановок. Число перестановок равно N! (N факториал):
Любой циклический алгоритм может быть построен с помощью команды «цикл-пока» (цикл с предусловием).
Формат оператора цикла с предусловием в Паскале: while do
Оператор, составляющий тело цикла, может быть простым или составным.
Вопросы и задания
1. Как блок-схемой и на алгоритмическом языке представляется команда цикла с предусловием?
2. Как программируется цикл с предусловием на Паскале?
3. Почему алгоритм вычисления N! должен быть циклическим?
4. Из каких этапов состоит работа программиста по решению задачи на компьютере?
5. Что такое математическая формализация задачи?
6. Что такое отладка программы? Что называется тестом?
7. Составьте алгоритм вычисления суммы всех натуральных чисел, не превышающих заданного натурального числа N. Проверьте алгоритм трассировкой. Напишите программу на Паскале.
8. Дано целое число X и натуральное N. Составьте алгоритм вычисления Xм. Проверьте алгоритм трассировкой. Напишите программу на Паскале.


Следующая страница Дополнительный материал к главе II (§§ 8 — 21). Программа перевода двоичного числа в десятичную систему счисления
Источник: xn—-7sbbfb7a7aej.xn--p1ai
Алгоритм евклида сообщение по информатике
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
Обозначим исходные данные как М u N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(М, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если M>N, то
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М u N (M> N). Это значит, что М = mК, N = nК, где m, n — натуральные числа, причем m > n. Тогда М — N = К(m — n), откуда следует, что К — делитель числа М — N. Значит, все общие делители чисел М и N являются делителями их разности М — N, в том числе и наибольший общий делитель.
Второе очевидное свойство:
Для «ручного» счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) заменить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
Получили: НОД(32, 24) =НОД(8, 8) = 8, что верно.
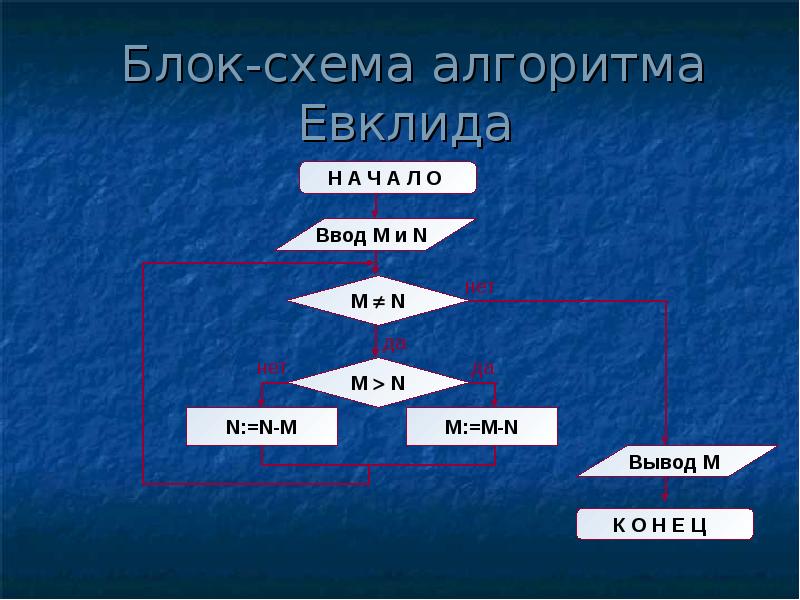
Описание алгоритма Евклида блок-схемой
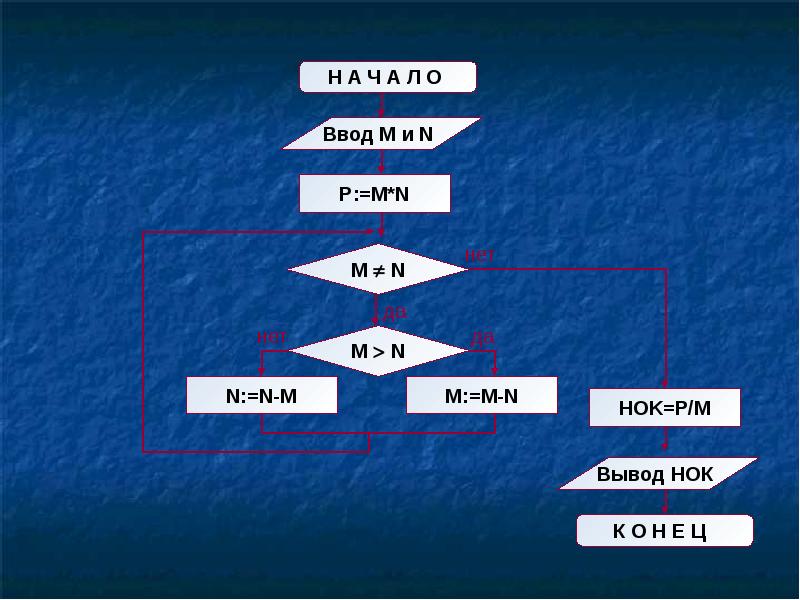
На рис. 3.12 приведена блок-схема алгоритма Евклида.
| Рис. 3.12. Блок-схема алгоритма Евклида |
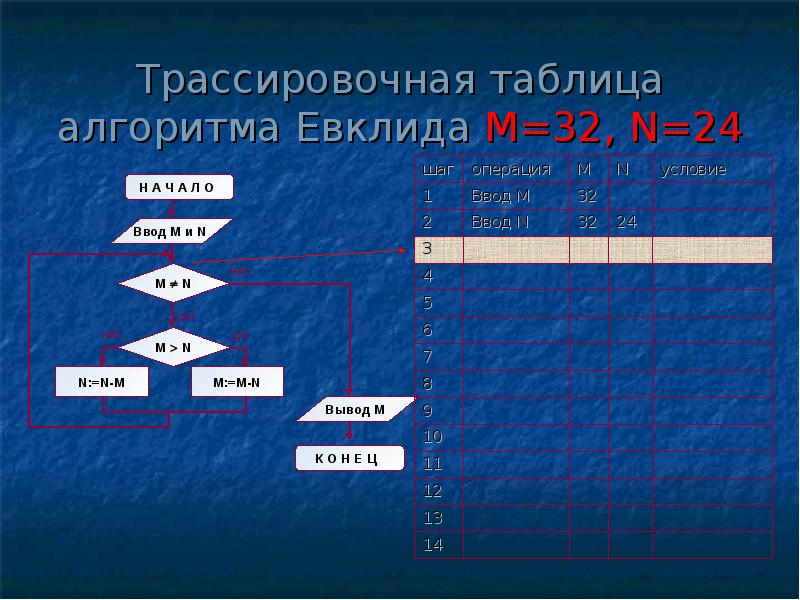
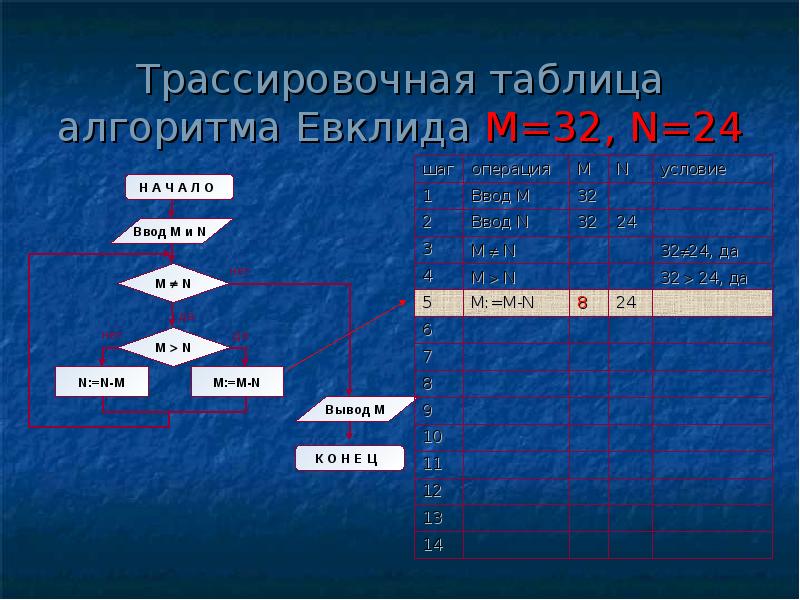
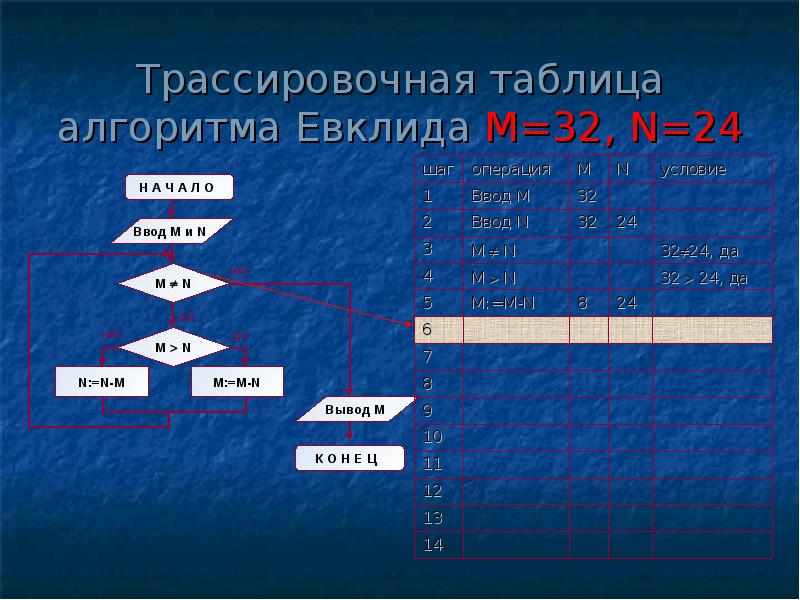
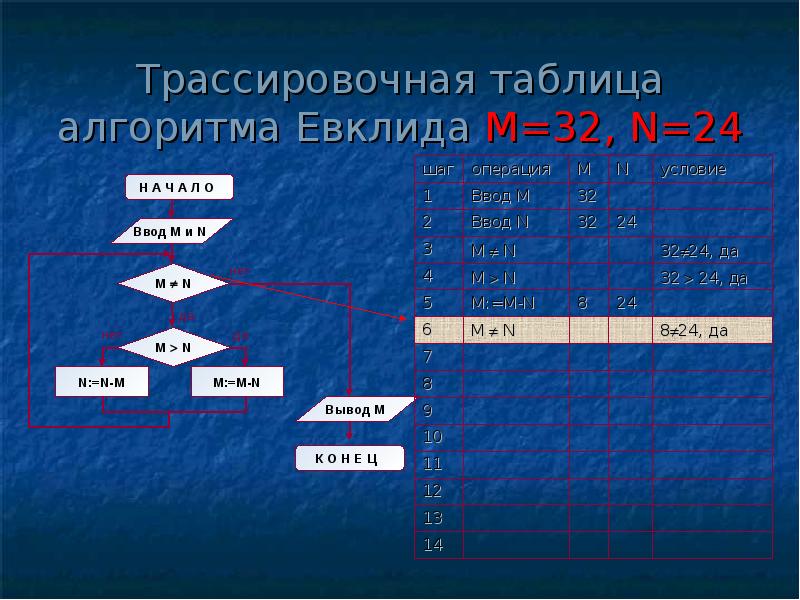
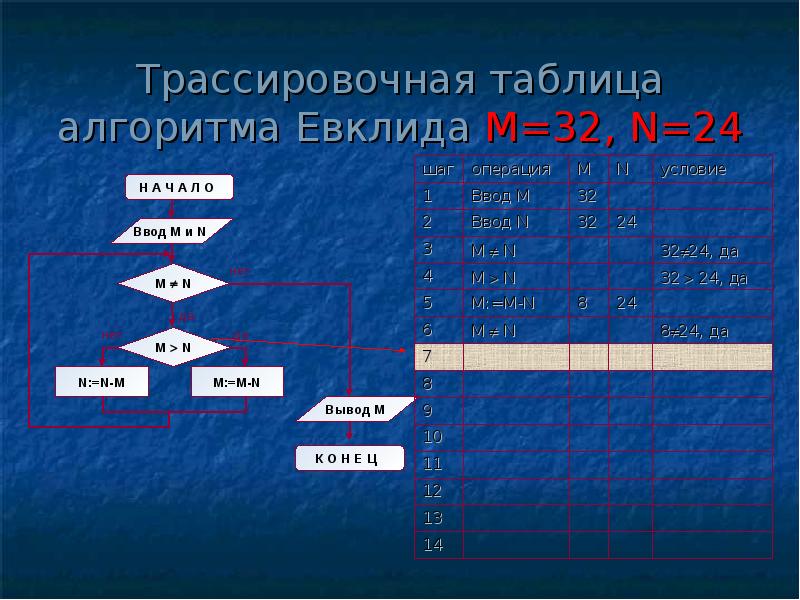
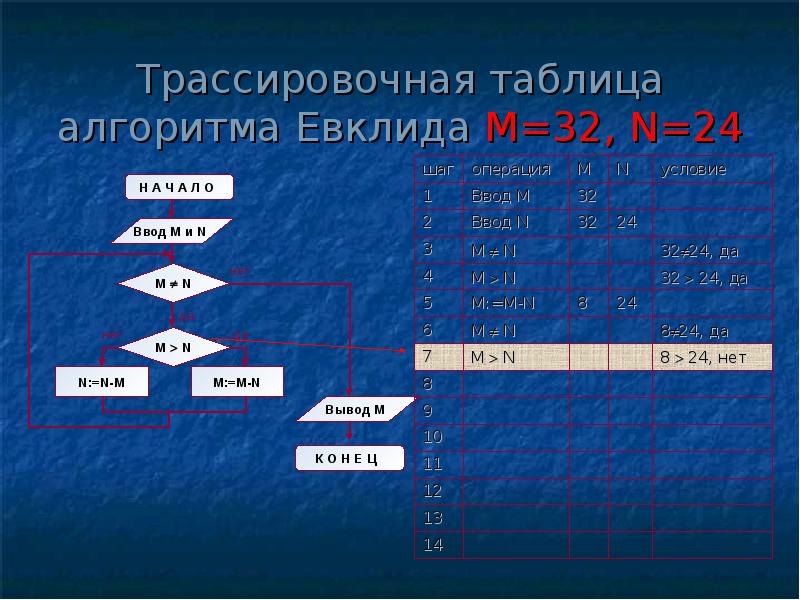
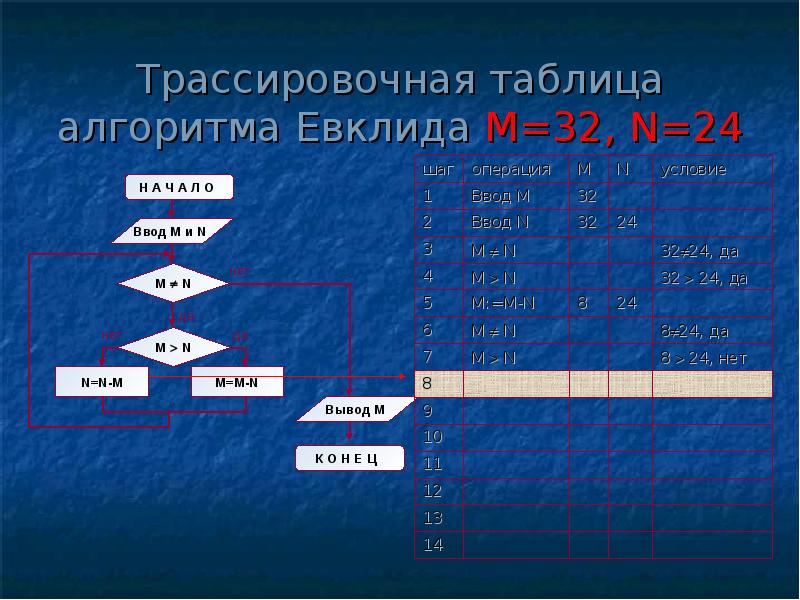
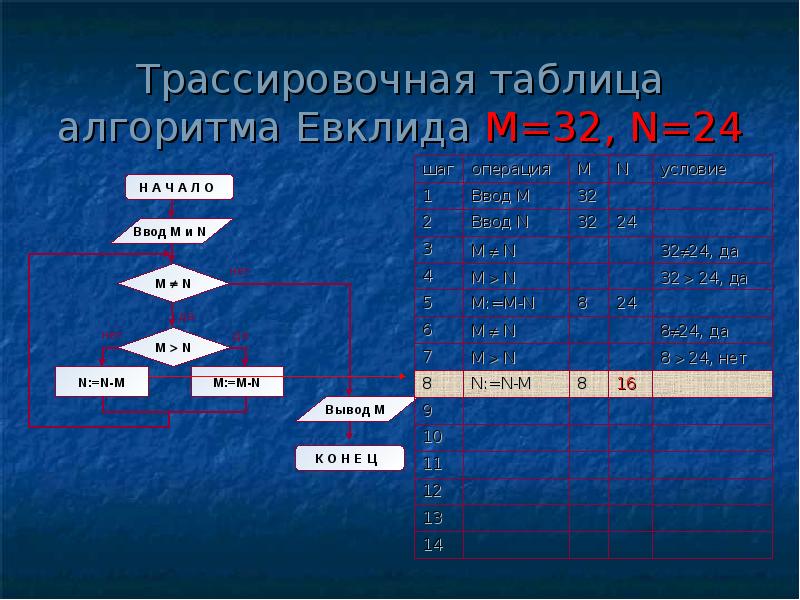
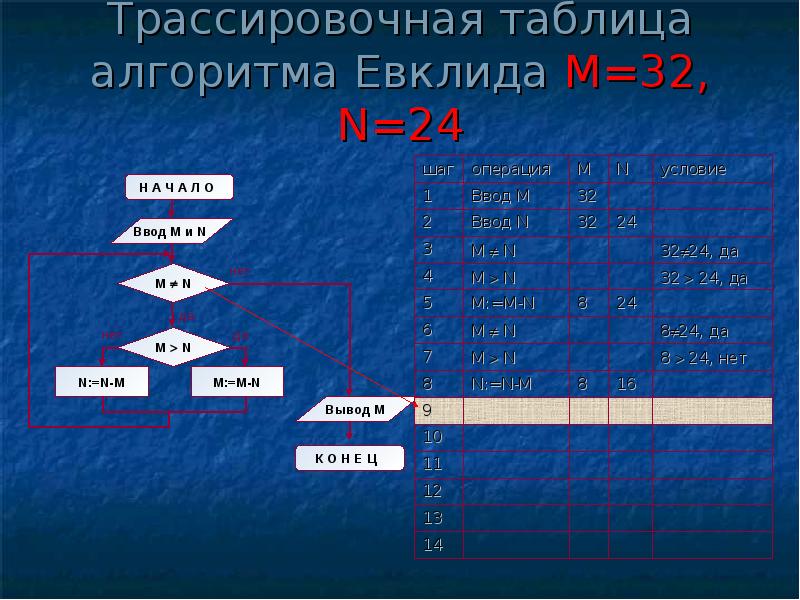
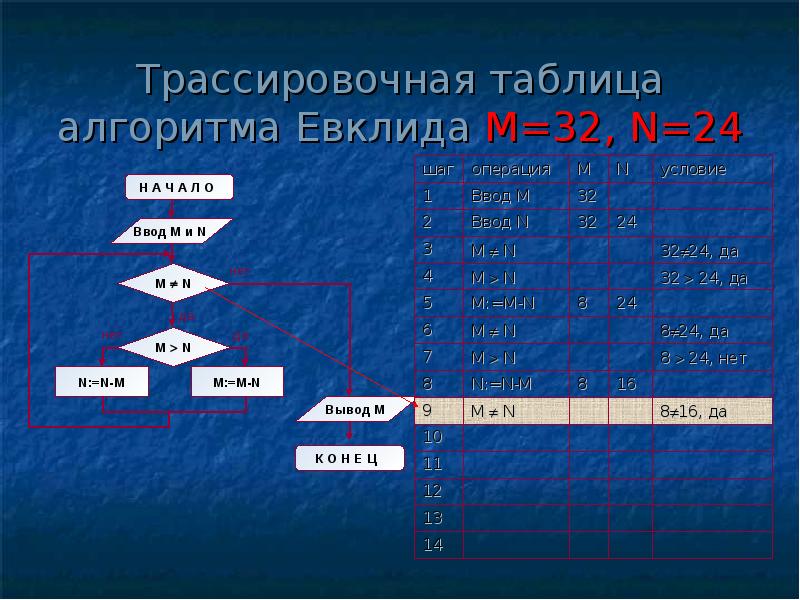
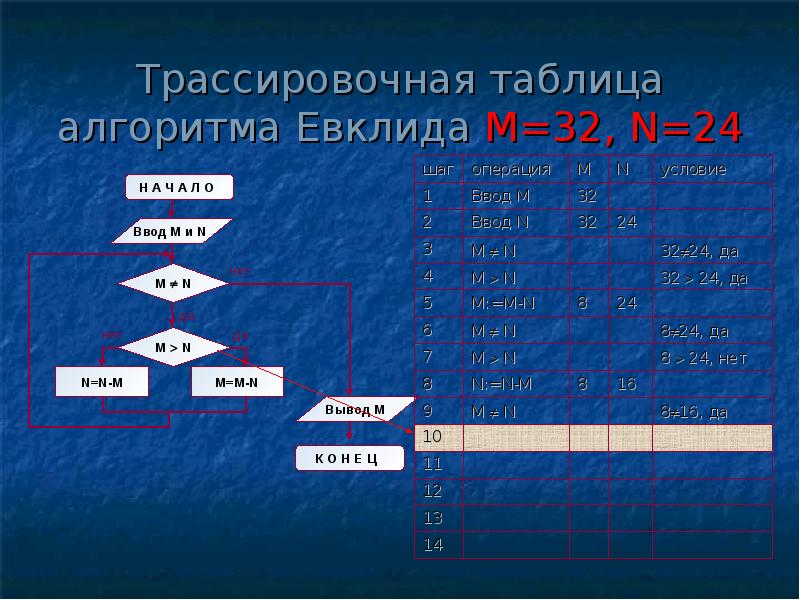
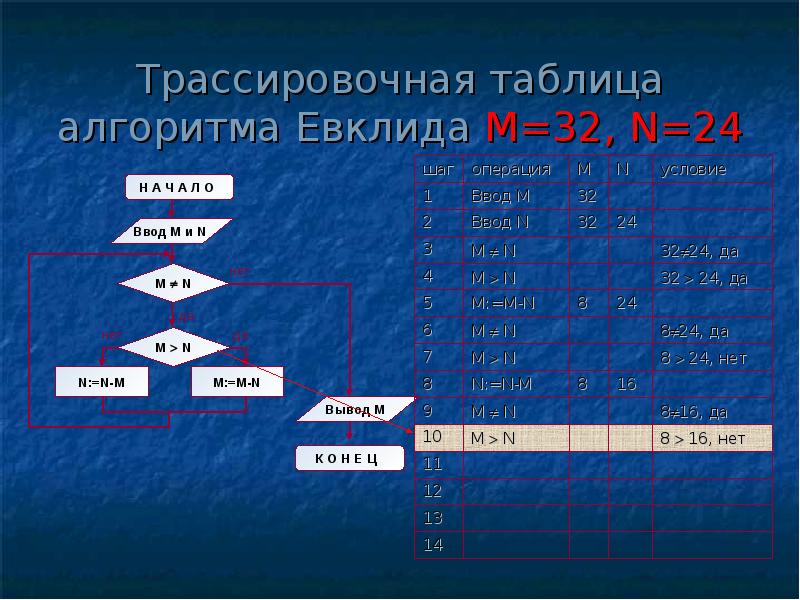
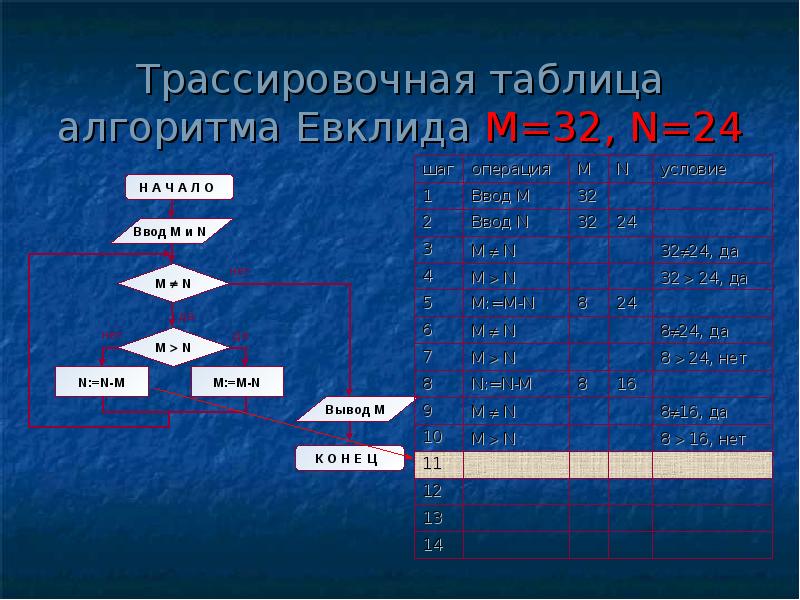
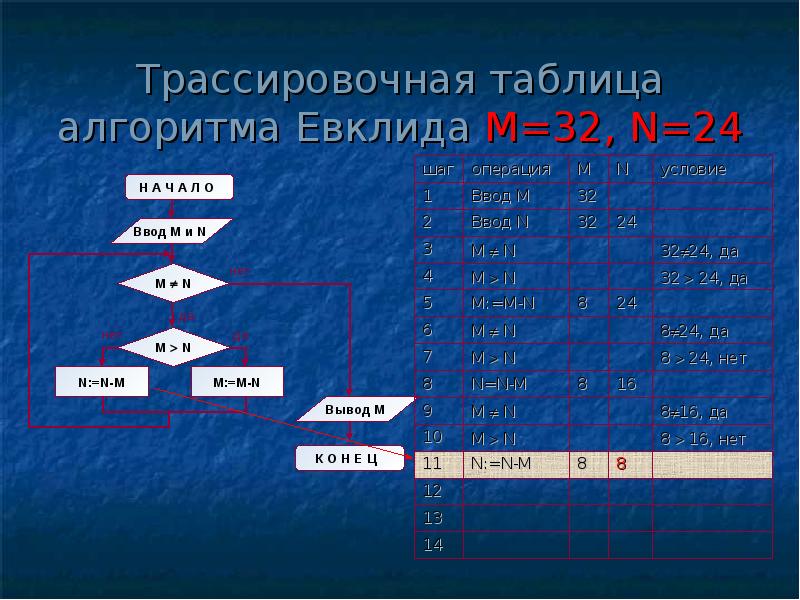
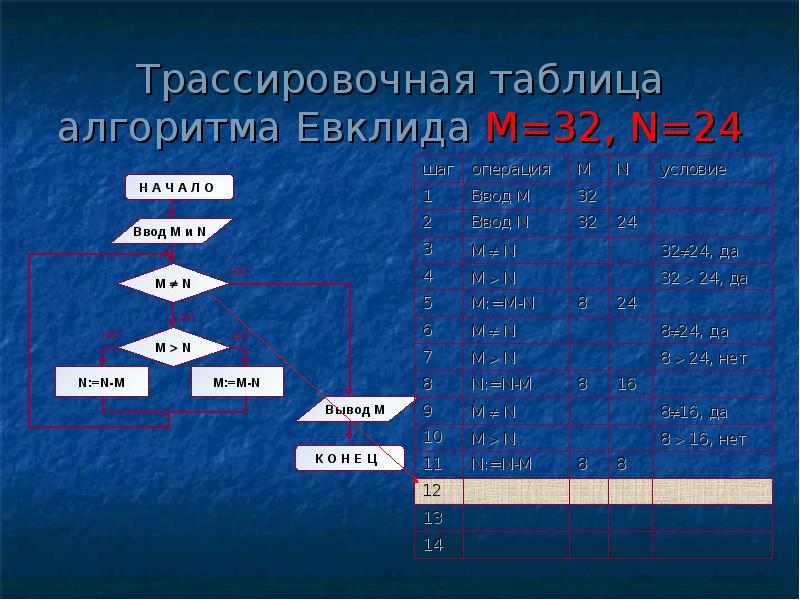
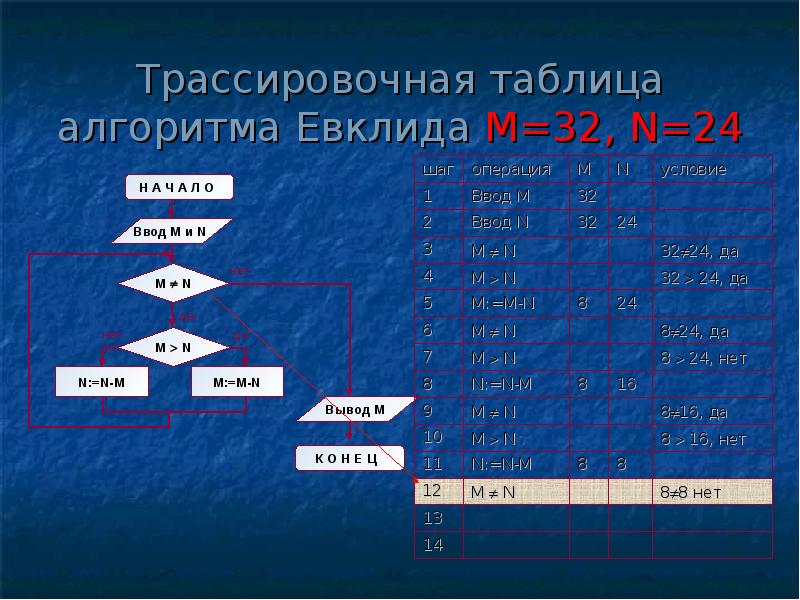
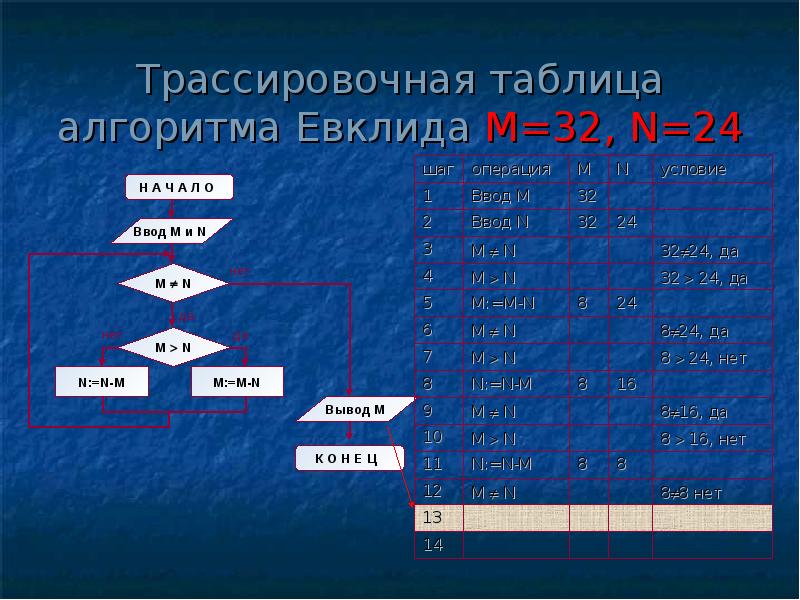
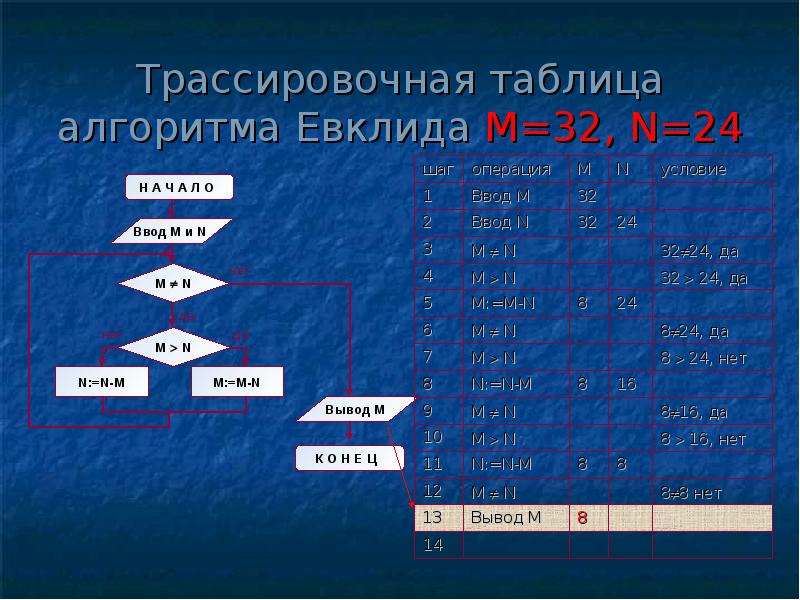
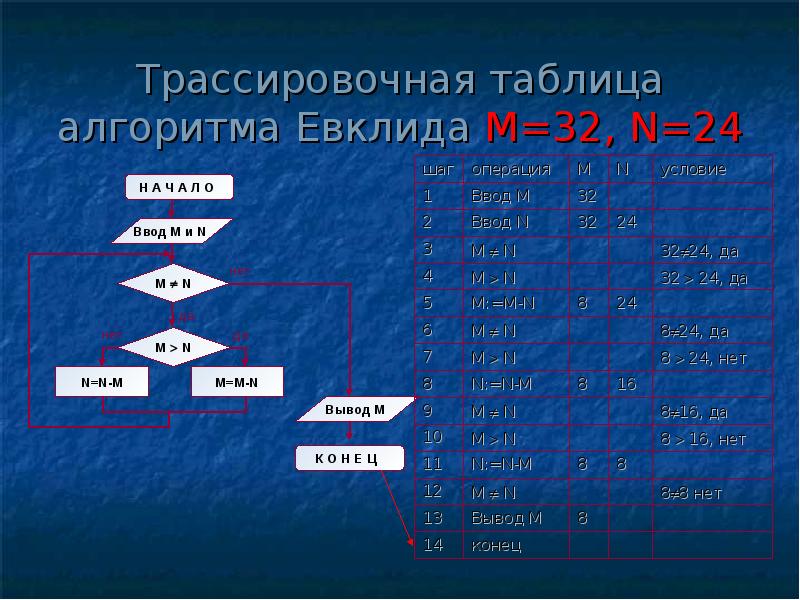
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24.
| Шаг | Операция | M | N | Условие |
| 1 | ввод М | 32 | ||
| 2 | ввод N | 24 | ||
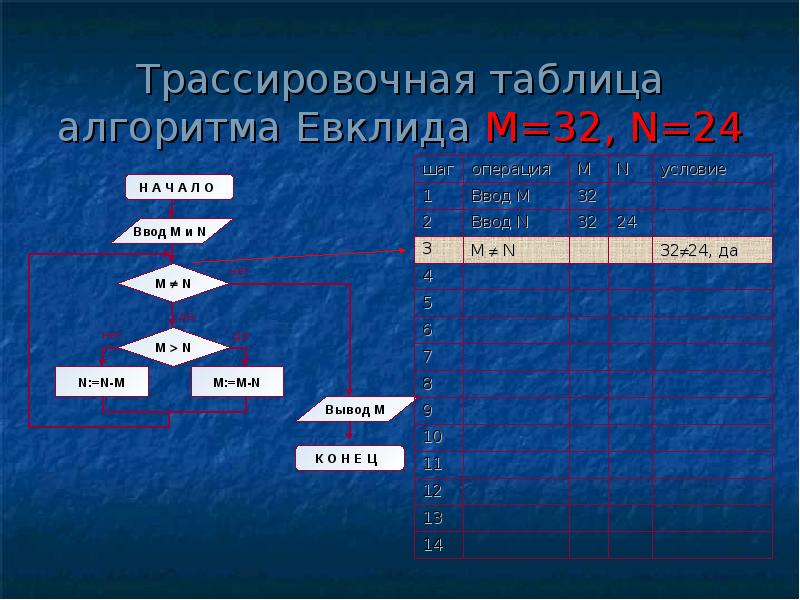
| 3 | M ¹ N | 32 ¹ 24, да | ||
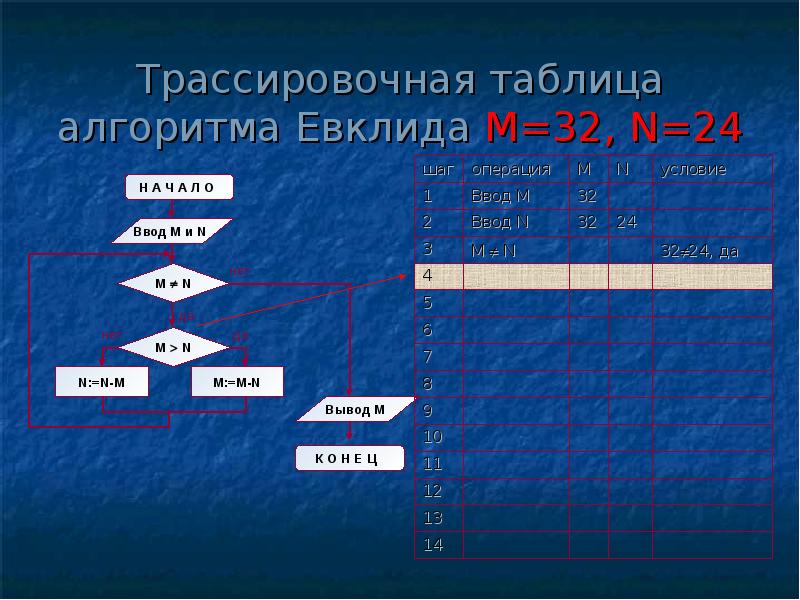
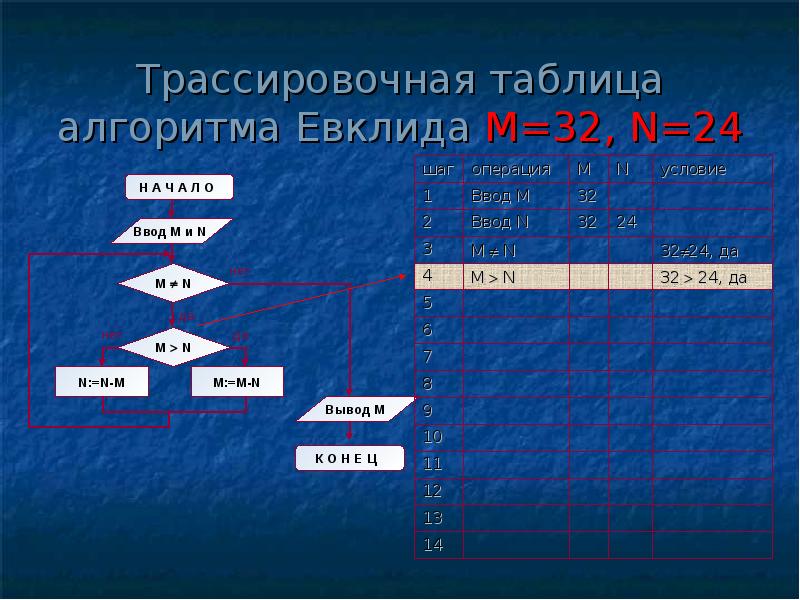
| 4 | M>N | 32>24, да | ||
| 5 | M:=M-N | 8 | ||
| 6 | M ¹ N | 8 ¹ 24, да | ||
| 7 | M>N | 8>24, нет | ||
| 8 | N:=N-M | 16 | ||
| 9 | M ¹ N | 8 ¹ 16, да | ||
| 10 | M>N | 8>16, нет | ||
| 11 | N:=N-M | 8 | ||
| 12 | M ¹ N | 8 ¹ 8, нет | ||
| 13 | вывод M | 8 | ||
| 14 | конец |
В итоге получился верный результат.
Программа на АЯ и на Паскале
Запишем алгоритм на АЯ и программу на Паскале.
| алг Евклид цел М, N нач вывод » Введите М и N» ввод М, N пока М N, повторять нц если M>N то M:=M-N иначе N:=N-M кв кц вывод «НОД 300»>Program Evklid; var M, N: integer; begin writeln(‘Введите М и N’); readln(M, N); while M<>N do begin if M>N then M:=M-N else N:=N-M end; write(‘Н0Д=’,М) end. |
1. Выполните на компьютере программу Evklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
Алгоритм Евклида- это алгоритм нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел.
Предварительный просмотр:
Подписи к слайдам:
АЛГОРИТМ ЕВКЛИДА ЕВКЛИД , древнегреческий математик. Работал в Александрии в 3 в. до н. э. Главный труд «Начала» (15 книг), содержащий основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов. Оказал огромное влияние на развитие математики. Работы по астрономии, оптике, теории музыки. Евклид (365-300 до. н. э.)
Вычисление НОД НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое оба исходных числа делятся без остатка. НОД( a , b )= НОД( a-b, b )= НОД( a, b-a) Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД. НОД ( 18 , 45 ) = НОД ( 18 , 45-18 ) = НОД ( 18 , 27 ) = НОД (18 , 9 ) = =НОД(9,9)=9 Пример :
ШАГ Операция M N Условие 1 Ввод M 48 2 Ввод N 18 3 M N 48 18, да 4 M>N 48>18, да 5 M:=M-N 30 6 M N 30 18, да 7 M>N 30 >18, да 8 M:=M-N 12 9 M N 12 18, да 10 M>N 12 >18, нет 11 N:=N-M 6 12 M N 12 6, да 13 M>N 12 >6, да 14 M:=M-N 6 15 M N 6 6, нет 16 Вывод M
program Evklid ; var m, n: integer; begin writeln (‘ vved 2 chisla ‘); readln ( m,n ); while m<>n do begin if m>n then m:=m-n else n := n-m ; end; write (‘nod=’,m); readln end.
0.Выполните на компьютере программу Evklid . Протестируйте её при значениях М=32, N=24; M=696, N=234. 1 . Проверить, являются ли два данных числа взаимно простыми. Примечание. Два числа называются взаимно простыми, если их наибольший общий делитель равен 1. 2 . Найти наименьшее общее кратное (НОК) чисел n и m , если НОК( n , m ) = n * m / НОД ( n , m ). 3 . Даны натуральные числа m и n . Найти такие натуральные p и q , не имеющие общих делителей, что p / q = m / n . 4. Найти НОД трех чисел. Примечание . НОД( a , b , c )= НОД(НОД( a , b ), c ) Задачи

Для иллюстрации основных алгоритмических конструкций в информатике и программировании часто применяют алгоритм Евклида. Применяя этот алгоритм, находят наибольший общий делитель двух целых чисел. Благодаря своей простоте и наглядности этот алгоритм не теряет популярности и по сей день.
Что такое алгоритм Евклида
Евклид жил в третьем веке до нашей эры в древней Греции. Он первым написал трактат по математике, в котором изложил основы планиметрии, стереометрии и теории чисел.

Рис. 1. Портрет древнегреческого математика Евклида.
Для понимания сути алгоритма вычисления НОД удобна его геометрическая трактовка.
Рассматриваются два отрезка разной длины. Из большего отрезка вычитают меньший, и затем больший отрезок заменяют результатом проведенного вычитания. Это действие выполняют несколько раз, пока отрезки не станут одинаковой длины. Полученная величина отрезков и есть наибольший общий делитель.
Этапы алгоритма Евклида
Процесс вычисления наибольшего общего делителя двух чисел удобно представить в виде цепочки шагов.
Построчная запись алгоритма Евклида
- Определиться со значением первого числа X.
- Определиться со значением второго числа Y.
- Если X≠Y, то выполнять пункт 4, иначе перейти к пункту 5.
- Если X>Y, то заменить X на X-Y и перейти к пункту 3, иначе заменить Y на Y- X и перейти к пункту 3.
- Считать Х наименьшим общим делителем.
В рассмотренной последовательности используются условные конструкции и конструкция повтора.
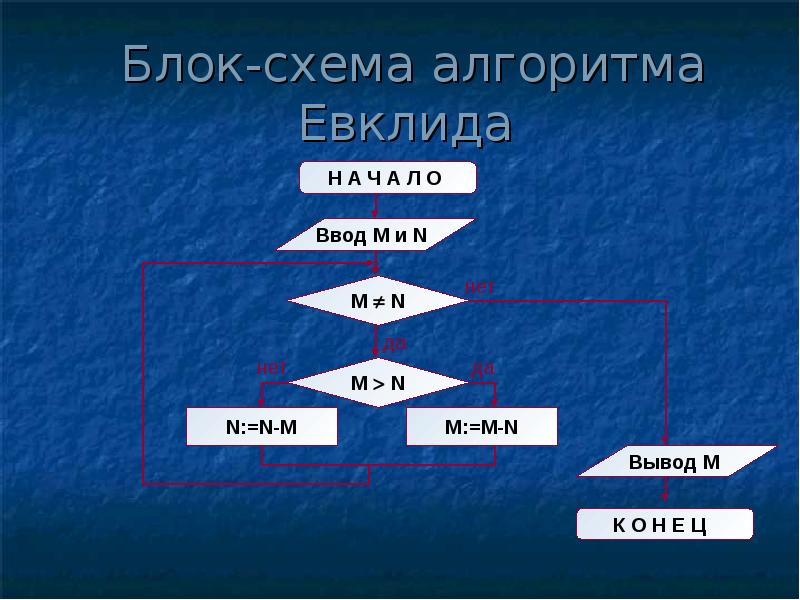
Для наглядного представления алгоритма Евклида используется блок-схема.
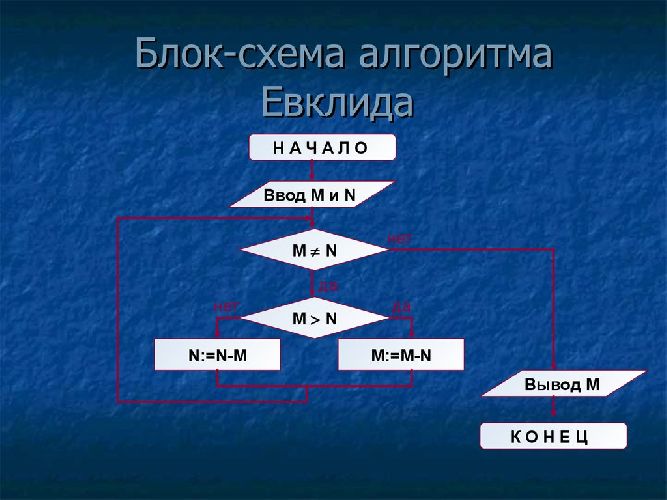
Рис. 2. Блок схема нахождения НОД по алгоритму Евклида.
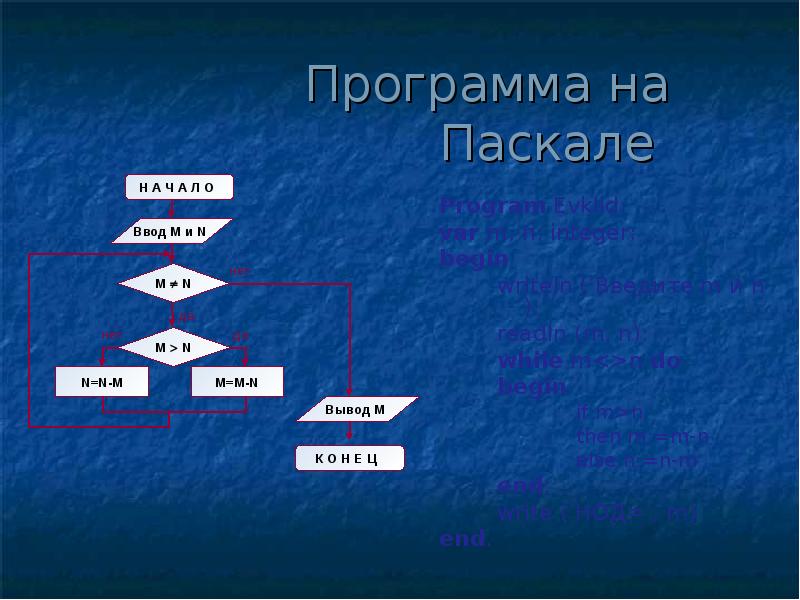
Запись алгоритма Евклида на языке Паскаль
Рис. 3. Логотип интегрированной среды разработки TurboPascal.
При записи алгоритма Евклида на процедурном языке программирования Паскаль необходимо строго придерживаться структуры программы. Начинать программу необходимо с заголовка, записывая ключевое слово PROGRAM и название программы. Пусть программа называется EVKLID. В конце первой строки ставится точка с запятой.
Этот знак следует ставить в конце каждой строки программы, а точнее после каждого оператора, процедуры или функции. Отсутствие его приведет к ошибке при отладке программы.
При записи алгоритма на языке программирования следует помнить правила использования ключевых слов, всегда описывать предварительно используемые переменные и не допускать синтаксических ошибок.
Описание переменных
В алгоритме используется всего две переменные X и Y, которые следует описать в разделе описания переменных, задавая им целый тип.
Var X, Y : integer;
Основная часть программы, в которой производятся все вычисления, заключается в операторные скобки begin и end. В конце программы обязательно ставится точка.
Ввод переменных с клавиатуры
Часть программы, предназначенная для ввода чисел, может выглядеть так:
write(‘Введите первое число X = ‘);
write(‘Введите второе число Y = ‘);
Организация повтора
Операцию вычитания в соответствии с алгоритмом следует выполнять до тех пор, пока выполняется условие неравности переменных X и Y. При равенстве X и Y повтор следует прекратить. Искомое число найдено.
Для реализации цикла, в котором итерации выполняются в соответствии с условием, удобнее всего использовать оператор с предусловием WHILE..DO. В решаемой задаче эта часть программы будет выглядеть так:
Запись условной конструкции на языке Паскаль
Условие на языке Паскаль записывается с помощью оператора IF..THEN..ELSE.
if X > Y then X:= X – Y else Y:= Y – X;
И в завершении программы, искомый результат выводится на экран.
Writeln (‘НОД чисел X и Y равен ‘, X);
Весь текст программы будет иметь вид:
Var X, Y : integer;
write(‘Начните вводить первое число X = ‘);
write(‘Начните вводить второе число Y = ‘);
if X > Y then X:= X – Y else Y:= Y – X;
Writeln (‘НОД чисел X и Y равен ‘, X);
Что мы узнали?
Для расчета наибольшего общего делителя двух целых чисел уже более тысячи лет используется простой и наглядный алгоритм, придуманный древнегреческим ученым Евклидом. Он хорошо иллюстрирует работу условных и циклических операторов в языке Паскаль.
Вы можете изучить и скачать доклад-презентацию на тему Алгоритм Евклида. Презентация на заданную тему содержит 41 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!











Постановка задачи: Требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел
Алгоритм нахождения НОД Разложить числа на простые множители. Найти общие множители. Найти их произведение.
Алгоритм Евклида Если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма. Заменить большее число разностью большего и меньшего из чисел. Вернуться к выполнению п. 1.
- Сообщение с гайморовой пазухой
- Сообщение водные объекты лнр
- Сообщение на тему суп харчо
- Сообщение об археологическом памятнике савин 1
- Сообщение о зубре из красной книги
Источник: obrazovanie-gid.ru