Сегодня довольно легко столкнуться с недобросовестными школьными учебниками, в частности с учебниками по информатике. В главах, посвященных алгоритмам, вы можете найти непосредственно определение алгоритма. Не пояснение, о чем идет речь, не рассказ о предмете, а именно определение.
Причем выделенное жирным шрифтом, старательно обведенное в рамку и помеченное какой-нибудь заметной пиктограммой в виде восклицательного знака. Обычно приправлено всё это соусом из кучи обязательных и необязательных свойств, образуя в итоге феерический кавардак. Давайте попытаемся понять, что же такое алгоритм, почему мы не может дать ему конкретного определения и выясним, какие свойства являются обязательными, а какие нет.
Составителей учебников легко понять, ведь на самом деле строгого определения алгоритма не существует, и более того, такого определения быть не может. Но вместо попыток объяснить, что к чему, авторы подсовывают бедным ученикам еще одно задание по зубрежке бесполезных и неправильных терминов. Чтобы не быть голословным, приведу выдержку из одного весьма распространенного учебника:
Понятие алгоритма и его свойства. Алгоритмы и структуры данных.

В университетах дела обстоят получше, однако автору этих строк на курсе по математической логике и теории алгоритмов пришлось столкнуться все с тем же винегретом из определения алгоритма и его свойств. Разберемся, что тут не так.
Бесконечность не предел
Но перед этим немного вспомним математику. Из школьного курса математики мы знаем, что чисел существует бесконечно много — какое бы большое число мы не взяли, всегда можно прибавить единицу и получить число еще большее. Обычно в школе этим и ограничиваются.
В университете на курсе высшей математики нам расскажут, что бесконечности на самом деле бывают разные: множества, элементы которого можно пронумеровать натуральными числами считаются счётно-бесконечными. К таким множествам относят сами натуральные числа (числу 1 мы дадим номер один, числу 2 номер два и т.д.), целые числа — натуральные плюс ноль и отрицательные целые числа (первый номер отдаем нулю, второй — числу 1, третий — числу -1, то есть каждой положительное число k получает номер 2k, а каждое отрицательное число -m получает номер 2m + 1). К счетно-бесконечным множествам относят четные, нечетные и даже рациональные числа (числа представимые в виде несократимой дроби m/n, где m — целое, n — натуральное). Получается, что натуральных чисел ровно столько же, сколько четных, и, в то же время, ровно столько же, сколько целых. «Количество» (мощность) множества натуральных чисел обозначается символом ℵ0 (алеф-ноль).
Такой же трюк с нумерацией не пройдет для бесконечных непериодических дробей (иррациональных чисел). Допустим такое множество счетное, то есть элементы этого множества можно пронумеровать натуральными числами.
Тогда рассмотрим бесконечную десятичную дробь с нулевой целой частью, у которой первая цифра после запятой не равняется цифре на той же позиции у дроби с номером 1, вторая цифра не равняется цифре на второй позиции у дроби с номером 2 и т.д. Тогда полученная дробь будет заведомо отличаться от всех дробей хотя бы одной цифрой. Получается для нее не нашлось номера в нашей бесконечной нумерации! Примененная схема доказательства называется канторовским диагональным методом в честь придумавшего ее математика Георга Кантора.
Про бесконечные дроби
Не стоит делать ошибку, записывая в иррациональные числа все бесконечные дроби. Иррациональными являются только те числа, которые нельзя представить в виде несократимой дроби вида m/n. В десятичной системе счисления дроби 1/3 и 2/7 тоже окажутся бесконечными, однако их «бесконечность» обусловлена выбранной системой счисления. В системе счисления по основанию 21 эти дроби будут иметь конечное представление, а вот, например, дробь 1/2 окажется бесконечной (периодической).
Говорят, что множество бесконечных десятичных дробей имеет мощность континуум, которая обозначается символом ℵ1 (алеф-один). В дальнейшем нам понадобится следующее множество. Рассмотрим некоторый алфавит (конечное множество символов). Теперь представим множество всех конечных цепочек символов алфавита A*. Коль скоро алфавит конечен, и каждая цепочка конечна, то множество таких цепочек счетно (их можно пронумеровать натуральными числами).

На сколько велика бесконечность?
Допустим в наш алфавит вошли все придуманные на земле символы: русский алфавит, японские иероглифы, шумерская клинопись и т.д. Тогда в наше множество войдут все написанные когда-либо книги, все книги, которые будут написаны и все книги, которые никто не стал бы писать (например, хаотичные последовательности символов).
Кроме того, представим книгу, толщиной в Солнечную систему и диагональю листа равной диаметру Млечного Пути, набранную 12-м шрифтом. В наше придуманное множество войдут все такие книги, отличающиеся хотя бы одним символов, и не только они, ведь вселенная бесконечна! Кто мешает представить себе книгу, размером в миллиарды световых лет? А все такие книги?
Уже на этом этапе воображение может давать сбои, а ведь наше множество всего лишь счетное. Чтобы дополнить множество до континуума, нужно рассмотреть бесконечную книгу, по сравнению с которой, предыдущие книги — детские игрушки. Но и одной бесконечной книги нам не хватит, нужно рассмотреть все бесконечные книги.
Конструктивно оперировать континуальными бесконечностями невозможно. Даже работая со счетными множествами, мы не рассматриваем сами множества, а только говорим, что какой бы не был элемент N, всегда найдется элемент N+1. Если мы ставим себе прикладную задачу, появление в наших рассуждениях континуальной бесконечности должно служить нам «тревожной лампочкой»: осторожно, выход за пределы конструктивного.
Алгоритмы и вычислимость
Суть работы компьютера заключается в проведении некоторого вычисления — преобразования одной порции информации в другую порцию. Причем результатом работы не обязательно должно быть число, главное, чтобы информация была представлена в некоторой объективной форме. Обычно под такой формой имеют в виду конечные цепочки символов некоторого алфавита.
Получается, компьютерное вычисление есть некоторая функция в сугубо математическом смысле, с областью определения и значений в рассмотренном выше множестве A*. Именно тут возникают определенные проблемы. Если мы можем вычислить функцию, то можем записать промежуточные вычисления в виде текста. Более того, в виде тексте можно описать вообще правила вычисления.
Мы знаем, что множество всех текстов счетное. Однако выясняется, что множество всех функций над натуральными числами имеет мощность континуум. Если мы пронумеруем все тексты, то получается функций вида A* -> A* тоже континуум. Получается, что некоторые функции вычислимы, а некоторые нет.
Компьютер проводит свои вычисления, подчиняясь некоторой программе, которая воплощает собой конструктивную процедуру, или алгоритм. Не сложно догадаться, что алгоритм как раз и есть то правило, по которому вычисляется функция. Можно сказать, функция считается вычислимой, если для нее существует некоторый алгоритм.
Понятия алгоритм и вычислимая функция оказываются настолько заковыристыми, что некоторые составители учебной литературы не утруждают себя попытками разъяснить их суть. Дело в том, что определения алгоритма не существует, и кроме того, существовать не может, иначе пришлось бы выбросить на свалку целый раздел математики — теорию вычислимости. Попробуем разобраться более подробнее.
Частично-рекурсивные функции и тезис Черча
Все началось с того, что математик Давид Гильберт в 1900 году предложил список нерешенных на тот момент математических проблем. Позже выяснилось, что десятая проблема (проблема решения произвольного диофантового уравнения) оказалось неразрешимой, но для доказательства этого факта пришлось составить целую новую математическую теорию. Вопросами того, какие задачи можно конструктивно решить, и что такое конструктивное решение, занялись математики Курт Гедель, Стивен Клини, Алонсо Черч и Алан Тьюринг.

Как выяснилось выше, континуальные бесконечности не всегда подходят под конструктивные рассуждения, поэтому Гедель и Клини предложили рассматривать только функции натурального аргумента (при необходимости любые функции над счетными множествами можно привести к «натуральным функция» путем замены элементов множеств их номерами). Изучая вычислимость таких функций, Гедель, Клини, Аккерман и другие математики пришли к так называемому классу частично-рекурсивных функций.
В качестве определения этого класса рассматривается набор базовых, очень простых функций (константа, увеличение на единицу и проекция, которая сопоставляет функции многих аргументов один из ее аргументов) и операторов, позволяющих из функций строить новые функции (операторы композиции, примитивной рекурсии и минимизации). Слово «частичные» показывает, что эти функции определены лишь на некоторых числах. На остальных они не могут быть вычислены. Попытки расширить класс частично-рекурсивных функций ни к чему не привели, так как введение новых операций приводило к тому, что получалось множество функций, совпадающее с классом частично-рекурсивных. В дальнейшем Алонсо Черч отказался от попыток расширения этого класса, заявив, что, видимо:
Частично-рекурсивные функции соответствуют вычислимым функциям в любом разумном понимании вычислимости.
Это утверждение называют тезисом Черча. Стоит отметить, что тезис Черча не является теоремой или доказанным утверждением. Во-первых, не понятно, что такое «разумное понимание», во-вторых, превратив тезис Черча в доказанный факт, мы лишаем себя перспектив дальнейшего исследования вычислимости и механизмов вычислений. Никто, впрочем, не мешает попробовать определить такой набор операций, который был бы мощнее базиса для частично-рекурсивных функций. Только вот, до сих пор это никому не удавалось сделать.
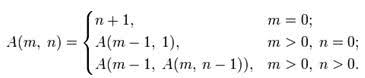
Формальная теория алгоритмов во многом построена аналогично теории вычислимости. Считается, что алгоритм есть некое конструктивное преобразование входного слова (цепочки символов некоторого алфавита) в некоторое выходное слово. Опять же, здесь мы имеем с функциями вида A*->A*.
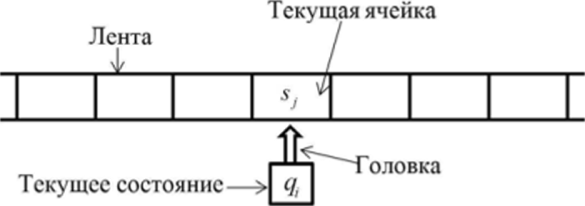
Конечно, предложенное описание не подходит под определение алгоритма, так как неясно, что же такое «конструктивное преобразование». Хоть понятия алгоритма и вычислимой функции близки, не стоит их смешивать. Для одного и того же алгоритма может быть предъявлено сколько угодно его записей на каком-нибудь формальном языке, но соответствующая вычислимая функция всегда одна. Один из основателей формальной теории алгоритмов, Алан Тьюринг, предложил формальную модель автомата, известного как машина Тьюринга. Тезис Тьюринга гласит:
Каково бы не было разумное понимание алгоритма, любой алгоритм, соответствующий такому пониманию, может быть реализован на машине Тьюринга.
Любые попытки построить более мощные автомат заканчивались неудачей: для каждого такого автомата (машина Поста, нормальные алгоритмы Маркова, автоматы с регистрами и несколькими лентами) удавалось построить аналогичную машину Тьюринга. Некоторые ученые объединяют тезис Черча и тезис Тьюринга в тезис Черча-Тьюринга, так как они весьма близки по духу.
Свойства алгоритмов
Алгоритм и программа определение и свойства
§ 27. Определение и свойства алгоритма
Основные темы параграфа:
♦ происхождение понятия «алгоритм»;
♦ исполнитель алгоритма;
♦ алгоритмический язык;
♦ свойства алгоритма;
♦ определение алгоритма;
♦ формальное исполнение алгоритма;
♦ что такое программа.
Понятие алгоритма так же фундаментально для информатики, как и понятие информации. Поэтому в нем очень важно как следует разобраться.
Происхождение понятия «алгоритм»
Само слово «алгоритм» происходит от имени выдающегося математика средневекового Востока Мухаммеда аль-Хорезми (787-850). Им были предложены приемы выполнения арифметических вычислений с многозначными числами (вам они хорошо знакомы из школьной математики). Позже в Европе эти приемы назвали алгоритмами, от Algorithmi — латинского написания имени аль-Хорезми. В наше время понятие алгоритма понимается шире, не ограничивается только арифметическими вычислениями.
Исполнитель алгоритма
Из предыдущего параграфа вы узнали, что алгоритм — это последовательность команд управления каким-либо объектом. Мы назвали его объектом управления или исполнителем алгоритма. Им может быть как техническое устройство, так и живое существо.
Рассмотрим исполнителя-человека. Для него можно сформулировать множество алгоритмов, например алгоритмы арифметических вычислений. С таким же успехом можно назвать алгоритмами множество различных инструкций, предписывающих последовательность действий человека для выполнения какой-либо работы. Например, кулинарный рецепт — это алгоритм работы повара с целью приготовления блюда; инструкция по сборке машинки из деталей детского конструктора — алгоритм для ребенка; инструкция по использованию кухонного комбайна — алгоритм для домохозяйки.
Вы, наверное, никогда не задумывались над тем, какое количество алгоритмов вам известно. Жизненный опыт человека растет с увеличением числа освоенных им алгоритмов. Например, чтобы ребенок научился покупать в магазине хлеб, ему нужно сначала рассказать (а лучше показать), как это делается. Освоив «алгоритм покупки хлеба», он в дальнейшем будет успешно выполнять эту работу.
Поиск выигрышной тактики, а следовательно, и алгоритма несложной игры — интересная и полезная задача. Рассмотрим одну из таких игр, которая называется игрой Баше.
Играют двое. Перед ними 21 предмет, допустим, камни (также может быть 11, 16, 26 и т. д.). Игроки берут камни по очереди. За один ход можно взять 1, 2, 3, 4 камня. Проигрывает тот, кто забирает последний камень.
Имеется выигрышная тактика для игрока, берущего камни вторым. Она заключается в том, чтобы брать такое количество камней, которое дополняет число камней, взятых соперником на предыдущем ходе, до пяти. Этот алгоритм можно описать в виде последовательности команд:
алг Игра Баше
нач
1. Предоставить ход сопернику.
2. Взять столько камней, чтобы в сумме с предыдущим ходом соперника получилось 5.
3. Если остался один камень, то объявить о своем выигрыше, иначе вернуться к выполнению команды 1.
кон
Игрок, строго следующий этому алгоритму, будет всегда выигрывать, даже если он не понимает, почему так происходит.
Алгоритмический язык
В приведенном примере используется символика учебного Алгоритмического языка (АЯ).
Из примера видно, что при записи алгоритма на АЯ в начале пишется заголовок, начинающийся со служебного слова алг (сокращенное слово «алгоритм»). Затем указывается название алгоритма, которое составитель алгоритма придумывает сам. Следующая часть называется телом алгоритма. Она начинается со служебного слова нач (начало) и заканчивается словом кон (конец). Тело алгоритма представляет собой последовательность команд для исполнителя.
Здесь и в дальнейшем служебные слова в алгоритмах на алгоритмическом языке будут записываться жирным шрифтом. В языках программирования (как и в АЯ) служебными называются слова, которые всегда употребляются в одном и том же смысле.
Свойства алгоритма
Процесс решения задачи должен быть разбит на последовательность отдельно выполняемых шагов.
Это свойство алгоритма называется дискретностью.
Всякий алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Для того чтобы алгоритм был выполним, нельзя включать в него команды, которые исполнитель не в состоянии выполнить. Нельзя повару поручать работу токаря, какая бы подробная инструкция ему ни давалась. У каждого исполнителя имеется свой перечень команд, которые он может исполнить. Такой перечень называется системой команд исполнителя алгоритмов (СКИ).
Алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые входят в систему команд исполнителя.
Это свойство алгоритма называется понятностью.
Каждая команда алгоритма должна определять однозначное действие исполнителя.
Это свойство алгоритма называется точностью.
Алгоритм не должен быть рассчитан на принятие каких-либо самостоятельных решений исполнителем, не предусмотренных составителем алгоритма.
Еще одно важное требование, предъявляемое к алгоритму — это свойство конечности (иногда говорят — результативности) алгоритма. Это значит, что:
Исполнение алгоритма должно завершиться за конечное число шагов.
Для успешного выполнения любой работы мало иметь ее алгоритм. Всегда требуются еще какие-то исходные данные, с которыми будет работать исполнитель (продукты для приготовления блюда, детали для сбора технического устройства и т. п.). Исполнителю, решающему математическую задачу, требуется исходная числовая информация. Задача всегда формулируется так: дана исходная информация, требуется получить какой-то результат. В математике вы привыкли в таком виде записывать условия задач. Например:
Дано: катеты прямоугольного
треугольника а = 3 см; b = 4 см.
Найти: гипотенузу с
Алгоритм решения этой задачи можно представить в таком виде:
алг Гипотенуза
нач
1, Возвести а в квадрат.
2. Возвести b в квадрат.
3. Сложить результаты действий 1 и 2.
4. Вычислить квадратный корень результата действия 3 и принять его за значение с.
кон.
Каждую из этих команд может выполнить любой человек, знающий основы математики, следовательно, они входят в его систему команд.
Еще пример: для поиска номера телефона нужного вам человека исходными данными являются: фамилия, инициалы человека и телефонная книга (точнее, информация, заключенная в телефонную книгу). Однако этого может оказаться недостаточно. Например, вы ищете номер телефона А. И. Смирнова и обнаруживаете, что в книге пять строк с фамилией «Смирнов А. И». Ваши исходные данные оказались неполными для точного решения задачи (вместо одного номера телефона вы получили пять). Оказалось, что нужно знать еще домашний адрес.
Набор: «фамилия — инициалы — телефонный справочник — адрес» является полным набором данных в этой ситуации.
Только имея полный набор данных, можно точно решить задачу.
Если исходные данные неполные, то задачу либо совсем нельзя решить (ничего нельзя узнать про гипотенузу по одному катету), либо получается неоднозначное решение (пять номеров телефонов).
В задачах управления физическими объектами (автомобиль, самолет, станок и т. п.) исходными данными является информация о состоянии объекта управления, об обстановке, его окружающей.
Определение алгоритма
Обобщая все сказанное, сформулируем определение алгоритма.
Алгоритм — понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящую от исходных данных к искомому результату.
Формальное исполнение алгоритма
Если алгоритм обладает перечисленными выше свойствами, то работа по нему будет производиться исполнителем
формально (то есть без всяких элементов творчества с его стороны). На этом основана работа программно управляемых исполнителей-автоматов, например промышленных роботов. Робот-манипулятор может выполнять работу токаря, если он умеет выполнять все операции токаря (включать станок, закреплять резец, перемещать резец, замерять изделие). От исполнителя не требуется понимания сущности алгоритма, он должен лишь точно выполнять команды, не нарушая их последовательности.
Что такое программа
А что такое программа? Отличается ли чём-то программа от алгоритма?
Программа — это алгоритм, записанный на языке исполнителя.
Иначе можно сказать так; алгоритм и программа не отличаются по содержанию, но могут отличаться по форме.
Для алгоритма строго не определяется форма его представления. Алгоритм можно изобразить графически, можно — словесно, можно — какими-нибудь специальными значками, понятными только его автору. Но программа должна быть записана на языке исполнителя.
Коротко о главном
Слово «алгоритм» происходит от имени Мухаммеда аль-Хорезми, первым предложившего приемы выполнения арифметических операций с многозначными числами.
Исполнитель алгоритма — это тот объект, для управления которым составлен алгоритм.
Процесс решения задачи должен быть разбит на последовательность отдельных шагов (свойство дискретности алгоритма).
Система команд исполнителя (СКИ) — это вся совокупность команд, которые исполнитель умеет выполнять (понимает). Алгоритм можно строить только из команд, входящих в СКИ исполнителя (свойство понятности).
Каждая команда алгоритма управления определяет однозначное действие исполнителя (свойство точности).
Выполнение алгоритма должно приводить к результату за конечное число шагов (свойство конечности).
Для успешного выполнения работы, решения задачи необходимо сообщить (передать) исполнителю полный набор исходных данных.
Выполнение алгоритма исполнителем производится формально.
Программа от алгоритма может отличаться по форме, но не по содержанию. Программа — это алгоритм, представленный на языке исполнителя.
Вопросы и задания
1. Что такое алгоритм? Откуда произошла это слово?
2. Что такое исполнитель алгоритма?
3. Что такое система команд исполнителя?
4. В чем заключаются основные свойства алгоритма?
5. Назовите исполнителей следующих видов работы: уборка мусора во дворе; перевозка пассажиров; выдача заработной платы; прием экзаменов; сдача экзаменов; обучение детей в школе. Попробуйте сформулировать СКИ для каждого из этих исполнителей.
6. Определите полный набор данных для решения следующих задач обработки информации:
• вычисление стоимости покупок в магазине;
• вычисление суммы сдачи от данных вами продавцу денег;
• определение времени показа по телевизору интересующего вас фильма;
• вычисление площади треугольника;
• определение времени падения кирпича с крыши дома;
• определение месячной платы за расход электроэнергии;
• перевод русского текста на итальянский язык;
• перевод итальянского текста на русский язык.
7. Попробуйте сформулировать алгоритмы обработки информации для заданий из п. 6, если исполнителем являетесь вы сами. Какие команды при этом вы должны уметь выполнять?
И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов
Сборник конспектов уроков информатики, учебная программа по информатике 9 класс, материалы для подготовки к урокам, готовые домашние задания
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Источник: edufuture.biz
Алгоритм в информатике — виды, структура и свойства

С помощью компьютера специалисты по информационным системам записывают новые программы, а также анализируют работу и исправляют ошибки в уже имеющихся. Но всё это невозможно совершить без знания алгоритмов. В информатике к изучению этого понятия приступают ещё в школе. Ученики получают первое представление о разных видах алгоритмов, их свойствах и способах создания.

Особенности понятия
Алгоритмы появились вместе с математикой, а первые упоминания о них встречаются в книге математика Мухаммеда бен Мусы аль-Хорезми из города Хорезма. Он описал методы выполнения различных действий с многозначными числами еще в 825 году. Само слово «алгоритм» появилось после того, как книгу ученого перевели на латинский язык в Египте.
Современное определение алгоритма в информатике — это описание действий, последовательное выполнение которых позволяет решить поставленную задачу за конкретное количество шагов.
С этим человек сталкивается каждый день, когда читает рецепты в кулинарных книгах, инструкции к различной технике, правила решения заданий. Но обычно все эти действия выполняются автоматически, без их анализа. Родители сталкиваются с этим понятием, когда объясняют детям, как открыть двери ключом или почистить зубы. Алгоритмов в окружающем мире множество, но есть общие признаки для всех их видов.
Свойства и виды
Для изучения понятия нужно разобраться в свойствах алгоритма в информатике. Их существует несколько:

- дискретность;
- детерминированность или определенность;
- понятность;
- завершаемость или конечность;
- массовость или универсальность;
- результативность.
Согласно свойству дискретности, алгоритмы должны описывать весь процесс решения задания в виде выполнения простых шагов. При этом на пункты отводится определенное количество времени. Каждый шаг должен определяться состоянием системы, то есть при одних и тех же исходных данных результат не меняется. Но есть и вероятностные алгоритмы, где пункты зависят от системы и случайно генерируемых чисел. В этой ситуации понятие становится подвидом обычного.
Понятность заключается в том, что команды алгоритма должны быть доступны конкретному исполнителю и входить в его личную систему. В ходе работы математическая функция при правильно заданных исходных данных выдает результат за определенное количество шагов. Иногда процедура может не завершиться, но вероятность таких случаев стремится к нулю.
Универсальность или массовость позволяет использовать алгоритм с разными наборами начальных данных. Последнее свойство обеспечивает его завершение в виде определенного числа — результата.
У каждого алгоритма есть свои начальные условия, цели и пути решения задачи. Существует большая разница между вычислительными и интерактивными видами. Происхождение первых связано с опытами ученого Тьюринга, они могут преобразовать входные данные в выходные. Вторые предназначены для связи с объектом управления, они работают только под внешним воздействием. Ученые выделяют несколько видов алгоритмов в информатике:
- детерминированные или жесткие;
- гибкие;
- линейные;
- разветвляющиеся;
- циклические;
- вспомогательные;
- структурные блок-схемы.

Жесткие еще называются механическими, так как чаще всего они используются для работы двигателя или машины. Они задают действия в единственно верной последовательности, что приводит к искомому или требуемому результату при условии выполнения процессов, для которых они и разработаны.
Гибкие алгоритмы делятся на эвристические и вероятностные. Первые используются при различных умственных выводах без строгих аргументов, а вторые дают возможность получить один результат несколькими способами.
Линейный тип — это набор команд, которые выполняются в строгой последовательности. Разветвляющийся включает хотя бы одно условие и при проверке дает разделение на несколько блоков. Появляются альтернативные ветвления программы.
В циклических видах несколько раз повторяются одни и те же действия, при этом меняются исходные данные. Сюда относятся переборы вариантов и бо́льшая часть способов расчета. Циклом в этом случае называют последовательность команд, которые нужно выполнить множество раз для достижения требуемого результата.

Подчиненный или вспомогательный вид является ранее разработанным алгоритмом для быстрого решения задачи. Он необходим для сокращения записи, если в структуре есть одинаковые команды. Схемами называются графические изображения с помощью блоков и соединяющих их прямых линий. Их используют перед программированием в качестве наглядных примеров, поскольку зрительное восприятие позволяет быстрее осмыслить процесс обработки информации и выявить возможные ошибки. В блоках отображаются исходные данные, которые вносятся в компьютер для вычислений.
Способы записи
Алгоритмы записываются несколькими методами. В информатике используется всего три:
- словесно-формульный;
- графический;
- программный.
В первом случае алгоритм записывается простым языком — словами и математическими формулами, что необходимо для понимания его теории. Здесь учитываются исходные данные, действия с ними и условия получения результата. Второй тип записи — компьютерное описание. Для этого применяются языки программирования и сами программы — форсы представления расчетов для их выполнения машиной.
Графическое описание состоит из связанных между собой географических фигур. Основные элементы блок-схем:
- прямоугольники;
- эллипсы;
- ромбы;
- шестиугольники;
- стрелки;
- пунктирные линии;
- соединительные фигуры.

В прямоугольниках записывают процессы, они указывают на выполнение операций, которые изменяют форму или значение данных. Ромбы содержат способы решения, здесь выбирается следующее направление в зависимости от поставленных условий. Модификации могут передаваться в шестиугольниках, где записываются операции, меняющие команды.
В блок-схемах можно выделить ручной ввод и предопределенные процессы. Первая фигура позволяет исполнителю ввести данные во время работы алгоритма через устройства, подключенные к компьютеру. Второе понятие заключается в использовании заранее записанных алгоритмов.
Графическое изображение содержит блоки документов и дисплеев. Оператор может вводить данные с бумаги и выводить их на нее, а также с помощью устройств, которые воспроизводят информацию на экране (проекторы для интерактивных досок, подключенные к компьютерам планшеты и ноутбуки).
Линии и соединительные фигуры указывают на связи между разными блоками и их последовательность. В схеме есть блоки начала и конца алгоритма, его прерывания, которое может произойти из-за сбоев в программе. Можно также указывать комментарии и пояснения исполнителя, для этого есть отдельные фигуры.
Правила создания

Существует несколько правил создания алгоритмов. Если их соблюдать, то в ходе работы всегда будет верный результат. Форма должна быть настолько простой, чтобы ее понял тот, кто занимается ее разработкой. Также не должно возникнуть проблем с чтением у того, кто будет выполнять описанные действия.
Объект, который проводит расчеты в алгоритме, называется исполнителем. Идеальными считаются роботы, компьютеры и другие машины. Они работают с программами, то есть схемами, написанными определенным языком программирования.
Разобраться с действиями помогут простые примеры алгоритмов по информатике. Когда есть ряд чисел от 1 до 100 и необходимо найти из них простые, то выбираются те, что делятся на единицу и себя. В этом случае используется циклическая структура:
- сначала нужно взять число 1;
- проверить, меньше ли оно, чем 100;
- если да, то узнать, простое ли оно;
- при выполнении условия записать;
- перейти к числу 2;
- повторить операцию.
Такие действия проводят со всеми числами. При этом первые четыре шага будут постоянно повторяться. Если попадается число, не являющееся простым (4, 6, 8 и т. д. ), то его нужно просто пропустить. Алгоритм в этом случае обладает предусловиями, то есть проверки происходят в начале цикла.
Анализ работы
Распространение информационных технологий привело к увеличению риска сбоев в работе программ. Предотвратить появление ошибок в алгоритмах можно с помощью доказательства их корректности математическими средствами. Такой анализ называется формальным методом, он предусматривает использование специального набора инструментов.

Гипотеза Ричарда Мейса утверждает, что избежать ошибок легче, чем их устранить. Благодаря доказательству корректности программ можно выявить их свойства, применяемые ко всем видам входных данных. Само понятие делится на две разновидности — частичную и полную. При первом типе корректности алгоритм дает правильный результат только для тех случаев, когда он завершается. Во втором случае программа завершает работу корректно для всего диапазона данных.
Исполнители во время проверки сравнивают выдаваемые данные со спецификой требуемого результата. Для доказательства корректности используются предусловия и постусловия. Первые должны выполняться перед включением программы, вторые — после завершения ее работы. Формальные методы успешно применяются для многих задач: верификации программ и микропроцессоров, разработки искусственного интеллекта, электронных схем и автоматических систем для железной дороги, спецификации стандартов.
Для выполнения алгоритма нужно только конкретное количество шагов, но на практике для этого потребуется много времени. В связи с этим введено понятие сложности. Она бывает временной, вычислительной и связанной с размерами алгоритма. Для увеличения эффективности используются быстрые программы, которые появились еще в 50-х годах прошлого века.
Источник: nauka.club