Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a >b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).
Python
#!/usr/bin/env python a = 18 b = 30 while a!=0 and b!=0: if a > b: a = a % b else: b = b % a print (a+b)
Perl:
sub nod
C:
int gcd(int a, int b) < int c; while (b) < c = a % b; a = b; b = c; >return abs(a); >
Pascal:
function nod( a, b: longint): longint; begin while (a <> 0) and (b <> 0) do if a >= b then a:= a mod b else b:= b mod a; nod:= a + b; end;
Java:
public class GCD < public static int gcd(int a,int b) < while (b !=0) < int tmp = a%b; a = b; b = tmp; >return a; > >
C#:
int gcd(int a, int b)
Алгоритм Евклида Паскаль 8 кл
Источник: habr.com
Алгоритм евклида программа на паскале
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НОД(12, 18) = 6.
Обозначим исходные данные как М u N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(М, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если M>N, то
НОД(М, N) = НОД(М — N, N).
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М u N (M> N). Это значит, что М = mК, N = nК, где m, n — натуральные числа, причем m > n. Тогда М — N = К(m — n), откуда следует, что К — делитель числа М — N. Значит, все общие делители чисел М и N являются делителями их разности М — N, в том числе и наибольший общий делитель.
Уроки Pascal. НОД (наибольший общий делитель)
Второе очевидное свойство:
Для «ручного» счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) заменить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
Получили: НОД(32, 24) =НОД(8, 8) = 8, что верно.
Описание алгоритма Евклида блок-схемой
На рис. 3.12 приведена блок-схема алгоритма Евклида.
| Рис. 3.12. Блок-схема алгоритма Евклида |
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24.
| Шаг | Операция | M | N | Условие |
| 1 | ввод М | 32 | ||
| 2 | ввод N | 24 | ||
| 3 | M ¹ N | 32 ¹ 24, да | ||
| 4 | M>N | 32>24, да | ||
| 5 | M:=M-N | 8 | ||
| 6 | M ¹ N | 8 ¹ 24, да | ||
| 7 | M>N | 8>24, нет | ||
| 8 | N:=N-M | 16 | ||
| 9 | M ¹ N | 8 ¹ 16, да | ||
| 10 | M>N | 8>16, нет | ||
| 11 | N:=N-M | 8 | ||
| 12 | M ¹ N | 8 ¹ 8, нет | ||
| 13 | вывод M | 8 | ||
| 14 | конец |
В итоге получился верный результат.
Программа на АЯ и на Паскале
Запишем алгоритм на АЯ и программу на Паскале.
| алг Евклид цел М, N нач вывод » Введите М и N» ввод М, N пока М N, повторять нц если M>N то M:=M-N иначе N:=N-M кв кц вывод «НОД 300»>Program Evklid; var M, N: integer; begin writeln(‘Введите М и N’); readln(M, N); while M<>N do begin if M>N then M:=M-N else N:=N-M end; write(‘Н0Д=’,М) end. |
Вопросы и задания
1. Выполните на компьютере программу Evklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
НОД(А, B, С) = НОД(НОД(А, В), С).
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
Источник: 5byte.ru
Алгоритм Евклида

Для иллюстрации основных алгоритмических конструкций в информатике и программировании часто применяют алгоритм Евклида. Применяя этот алгоритм, находят наибольший общий делитель двух целых чисел. Благодаря своей простоте и наглядности этот алгоритм не теряет популярности и по сей день.
Что такое алгоритм Евклида
В математике известен конструктивный алгоритм определения наибольшего общего делителя двух целых чисел, который носит название алгоритма Евклида. Греческий ученый математик Евклид первым описал этот алгоритм в своем научном трактате «Начала».
Евклид жил в третьем веке до нашей эры в древней Греции. Он первым написал трактат по математике, в котором изложил основы планиметрии, стереометрии и теории чисел.

Для понимания сути алгоритма вычисления НОД удобна его геометрическая трактовка.
Рассматриваются два отрезка разной длины. Из большего отрезка вычитают меньший, и затем больший отрезок заменяют результатом проведенного вычитания. Это действие выполняют несколько раз, пока отрезки не станут одинаковой длины. Полученная величина отрезков и есть наибольший общий делитель.
Этапы алгоритма Евклида
Процесс вычисления наибольшего общего делителя двух чисел удобно представить в виде цепочки шагов.
Построчная запись алгоритма Евклида
- Определиться со значением первого числа X.
- Определиться со значением второго числа Y.
- Если X≠Y, то выполнять пункт 4, иначе перейти к пункту 5.
- Если X>Y, то заменить X на X-Y и перейти к пункту 3, иначе заменить Y на Y- X и перейти к пункту 3.
- Считать Х наименьшим общим делителем.
В рассмотренной последовательности используются условные конструкции и конструкция повтора.
Для наглядного представления алгоритма Евклида используется блок-схема.
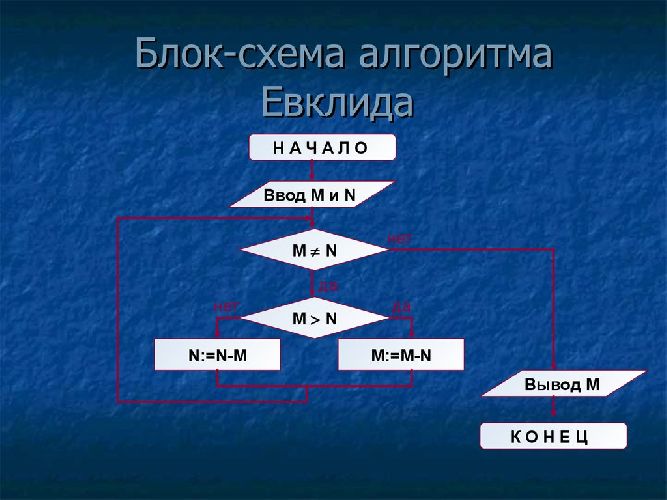
Запись алгоритма Евклида на языке Паскаль
При записи алгоритма Евклида на процедурном языке программирования Паскаль необходимо строго придерживаться структуры программы. Начинать программу необходимо с заголовка, записывая ключевое слово PROGRAM и название программы. Пусть программа называется EVKLID. В конце первой строки ставится точка с запятой.
Этот знак следует ставить в конце каждой строки программы, а точнее после каждого оператора, процедуры или функции. Отсутствие его приведет к ошибке при отладке программы.
При записи алгоритма на языке программирования следует помнить правила использования ключевых слов, всегда описывать предварительно используемые переменные и не допускать синтаксических ошибок.
Описание переменных
В алгоритме используется всего две переменные X и Y, которые следует описать в разделе описания переменных, задавая им целый тип.
Var X, Y : integer;
Основная часть программы, в которой производятся все вычисления, заключается в операторные скобки begin и end. В конце программы обязательно ставится точка.
Ввод переменных с клавиатуры
Значения переменных X и Y удобнее всего вводить с клавиатуры, используя процедуры ввода чисел с клавиатуры READLN. Перед вводом данных лучше вывести пользователю будущей программы сообщение «Введите число» с использованием процедуры вывода WRITELN.
Часть программы, предназначенная для ввода чисел, может выглядеть так:
write(‘Введите первое число X = ‘);
write(‘Введите второе число Y = ‘);
Организация повтора
Операцию вычитания в соответствии с алгоритмом следует выполнять до тех пор, пока выполняется условие неравности переменных X и Y. При равенстве X и Y повтор следует прекратить. Искомое число найдено.
Для реализации цикла, в котором итерации выполняются в соответствии с условием, удобнее всего использовать оператор с предусловием WHILE..DO. В решаемой задаче эта часть программы будет выглядеть так:
Запись условной конструкции на языке Паскаль
Условие на языке Паскаль записывается с помощью оператора IF..THEN..ELSE.
if X > Y then X:= X – Y else Y:= Y – X;
И в завершении программы, искомый результат выводится на экран.
Writeln (‘НОД чисел X и Y равен ‘, X);
Весь текст программы будет иметь вид:
Var X, Y : integer;
write(‘Начните вводить первое число X = ‘);
write(‘Начните вводить второе число Y = ‘);
if X > Y then X:= X – Y else Y:= Y – X;
Writeln (‘НОД чисел X и Y равен ‘, X);
Что мы узнали?
Для расчета наибольшего общего делителя двух целых чисел уже более тысячи лет используется простой и наглядный алгоритм, придуманный древнегреческим ученым Евклидом. Он хорошо иллюстрирует работу условных и циклических операторов в языке Паскаль.
Источник: obrazovaka.ru