Сложно сказать с чего начать построение или просто программирование роботов, но я бы начал с понимания алгоритмов. Не важно при этом какой язык вы будете изучать в дальнейшем или вообще будете аппаратно реализовывать (да, именно аппаратно можно решить большое количество задач и успешно решается в разных областях). Если погрузится в тему устройств, то у любого из них есть свои управляющие элементы, заложенные в них алгоритмы, и исполнительные элементы. Даже простые механические часы с боем или «кукушкой» имеют свой алгоритм.
Для начала предлагаю определиться с понятием алгоритма:
Алгоритмом называется строго определенная последовательность действий, определяющих процесс перехода от исходных данных к искомому результату.
Как иногда любят говорить технари — «машина тупая, как ты ей сказал, так она и сделала» и никак иначе. То есть при дублировании всех внутренних и внешних условий результат также будет дублироваться.
Но теперь непосредственно к алгоритмам.
ВСЯ СЛОЖНОСТЬ АЛГОРИТМОВ ЗА 11 МИНУТ | ОСНОВЫ ПРОГРАММИРОВАНИЯ
Не важно на каком языке вы планируете писать программу, так или иначе вы будете сперва продумывать алгоритм и только потом уже переходить к реализации.
Вы можете сказать, что для простых программ алгоритмы уже не нужны и все делается сразу в коде и даже простую сортировку можно написать не продумывая особо алгоритм. Но это только так кажется, так как даже выводя на печать текст простой командой (например print «Hello world» ) вы все равно используете алгоритм, который для вас кажется очевидным. Большое число начинающих программистов отказываются рисовать блок схемы, мотивируя это тем, что и так всё понятно. На простых реализациях, действительно всё просто. Но при усложнении программы или её нелинейной структуре содержать её в голове становится сложнее, особенно после продолжительного перерыва в работе с программой.
Свойства алгоритмов
Для того, чтобы алгоритм был рабочим и устойчивым необходимо определится с его свойствами:
Конечность — каждое действие алгоритма должно иметь возможность настоящего исполнения. Как и сам алгоритм в целом. Тогда алгоритм будет исполнимым — то есть конечным.
Детерминированность — четкое пошаговое разделение на понятные и однозначные шаги. То есть исключается неопределенность или неоднозначное толкование.
Результативность — алгоритм должен показывать результат или вывести информацию о не возможности реализации данного алгоритма, что тоже является результатом. Например невозможность делить на ноль, должна выявляться алгоритмом, а не ошибкой компилятора или интерпретатора.
Массовость — возможность применение алгоритма для целого класса задач, где могут отличаться только исходные данные. При этом стоит учесть, что сами данные входят в область реализации этого алгоритма. Например при подсчете общего объема груза, мы можем использовать только положительные числа и рассчитывать их исходя из массы и плотности даваемых нам на входе.
Дискретность — способность алгоритма по-шагово решать любую задачу, Каждый из шагов прост и понятен и требуется конечное время на его исполнение.
На самом деле эти свойства будут для вас очевидны при начальной работе и создании первых программ.
Какие способы представления алгоритмов бывают:
1. Графический способ . Один из самых удобных и популярных способов. Представление алгоритма в виде блоков и связей между ними, пример на картинке ниже.
Источник: dzen.ru
Алгоритмы (свойства, реализация алгоритмов)

Алгоритм решения задачи – это система точных и понятных предписаний о содержании и последовательности выполнении конечного числа действий, необходимых для решения любой задачи данного типа.
Алгоритм – это конечный набор правил, последовательное применение, которых к обрабатываемой информации за конечное число шагов позволяет получить результаты обработки (правила выполнения арифметических действий, правила решения определенных видов уравнений и т.д.).
Слово алгоритм появилось в результате искажения (после перевода на европейские языки) имени выдающего математика IX века Аль –Хорезми, которым были описаны правила выполнения основных арифметических действий в десятичной системе счисления. Понятие алгоритма возникло и используется ранее, чем появление ЭВМ.
Основные свойства алгоритма:
1. Дискретность, т.е. пошаговый характер определяемого им процесса. Описываемый процесс должен быть разбит на последовательность отдельных шагов. При каждом шаге работы алгоритма известно, что считать результатом шага.
2. Детерминированность (однозначность или определенность). Процесс применения правил к исходным данным определен вполне однозначно, результат работы алгоритма также будет однозначен. Запись алгоритма должна быть настолько четкой, полной, продуманной в деталях, чтобы у исполнителя не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма.
3. Массовость. Необходимы алгоритмы, обеспечивающие решение широкого класса задач данного типа. Они предполагают возможность использовать различные допустимые значения исходящих данных.
Например: решение уравнения ах2+вх+с=0 в области действительных чисел может быть найдено по формуле:
, которые применяемы не для одного, а для многих квадратных уравнений с коэффициентами а, в, с, удовлетворяющих условию
4. Результативность. При точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен быть получен какой-либо определенный ответ на вопрос задачи.
Под алгоритмизацией понимают процесс разработки алгоритма решения какой-либо задачи.
Формы (способы) записи алгоритмов:
1. Прочитать заданное значение х.
2. Умножить х на 8.
3. Из результата второго действия (шага) извлечь квадратный корень.
4. К результату третьего действия прибавить 1.
5. Умножить х на 3.
6. Результат пятого действия разделить на результат четвертого действия.
7. Записать значение результата у.
Недостатки: низкая наглядность и слабая формализация. Этим способом можно описывать алгоритмы с произвольной степенью детализации.
2. Формульно-словесный способ основывается на задании последовательных шагов алгоритма с помощью математических формул и выражений в сочетании со словесными выражениями. Например:
1. Если Х0, то перейти к шагу 2, в противном случае перейти к шагу 3.
2. Положить S= +D. Перейти к шагу 4.
3. Положить S=X-A. Перейти к шагу 4.
4. Принять S за искомый результат и остановиться.
Он более компактен и нагляден, но не является строго формальным.
B- ввод исходных данных
A- арифметический оператор
П — оператор печати (вывода)
Р — логический оператор
Я — оператор останова
Операторы имеют номера-индексы в соответствии с порядком их исследования. Логический оператор записывается как функция, аргументом которой служит проверяемое условие P (i=N) или P(? ?o)и т.д.
Операторы выполняются последовательно, которые могут нарушить логические операторы и безусловные операторы передачи управления. Если окажется, что проверяемое условие истинно, то очередным становится оператор, стоящий справа от логического оператора, в противном случае, когда логическое условие не соблюдается, оператор – приемник указывается стрелкой. Отсутствие передачи управления от оператора слева к соседнему оператору справа обозначается точкой с запятой (;). Алгоритм завершается оператором останова.
Операторная схема алгоритма сопровождается схемой счета.
Схема счета представлена в виде таблицы
| № | Символ-оператор | Содержание оператора |
| В1Р2 А3А4П5Я6 | Ввод исходных данныхПроверка выполнения логического условия (X0)Вычисление значения Вычисление значения S= X-AПечать вычисленного значения SОстанов | |
| Операторная схема выглядит следующим образом | B1 P2 (х0) А3; А4 П5 Я6 |
Ввел этот метод А.А. Ляпунов в 1954 году. Операторные схемы имеют формальный уровень, близкий к алгоритмическим языкам, и поэтому могут рассматриваться как средство автоматизации программирования.
4. Метод блок-схемы – это графическое изображение логической структуры алгоритма. На блок-схеме каждый этап процесса обработки представляется в виде геометрических фигур (блоков), имеющих определенную конфигурацию в зависимости от характера вычисляемых операций. Блоки соединяются стрелками, которые определяют последовательность их выполнения. Этот метод наиболее наглядный и удобный.
Основные виды блоков:
— начало, конец (останов)
— вывод на экран дисплея
5. Псевдокод или структурно-стилизованный способ записи алгоритма основан на формализованном представлении предписаний. Разновидность: алгоритмический язык в русской нотации. Это например:
Важнейшая особенность – близость к алгоязыкам программирования.
6. Язык программирования используется для записи алгоритмов в виде, непосредственно доступном ЭВМ.
Программа, написанная на языке программирования, представляет собой последовательность операторов, реализующих заданный алгоритм.
Языки программирования высокого уровня: ФОРТРАН, БЕЙСИК, КОБОЛ, АЛГОЛ, ПАСКАЛЬ, СИ, ПЛ/1 и др.
На языке Бейсик это выглядит следующим образом:
10 INPUT «Исх. данные», Х, D, А
20 IF X0 THEN 5 O
60 PRINT «Результат=», S
При создании нового алгоритма предоставляется так называемый, базовый алгоритм, что является минимально необходимым логическим набором для проведения: элементарных действий с данными. Базовый алгоритм состоит из четырех элементов:
3. элемент расчета;
4. конец алгоритма.
При этом, по умолчанию, третий элемент — элемент расчета необходим для того, чтобы явно указать передачу введенных данных в элементе ввода на конечный элемент алгоритма. Тем самым базовый алгоритм позволяет осуществлять передачу данных, получая их из вне, без какой-либо дополнительной математической обработки.
Структуры данных, применяемые в алгоритмах, могут быть чрезвычайно сложными. В результате выбор правильного представления данных часто служит ключом к удачному программированию и может в большей степени сказываться на производительности программы, чем детали используемого алгоритма. Вряд ли когда-нибудь появится общая теория выбора структур данных. Самое лучшее, что можно сделать,- это разобраться во всех вазовых кирпичиках и в собранных из них структурах. Способность приложить эти знания к конструированию больших систем — это прежде всего дело инженерного мастерства и практики.
Начиная изучение структур данных или информационных структур, необходимо ясно установить, что понимается под информацией, как информация передается и как она физически размещается в памяти вычислительной машины.
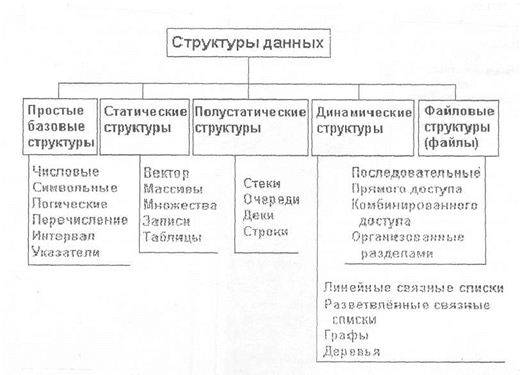
Информация по каждому типу однозначно определяет:
1) структуру хранения данных указанного типа, т ,e. выделение памяти и представление данных в ней, с одной стороны, и интерпретирование двоичного представления, с другой;
2) множество допустимых значений, которые может иметь тот или иной объект описываемого типа;
3) множество допустимых операций, которые применимы к объекту описываемого типа.
В вычислительной технике структура данных — это программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных. Для добавления, поиска, изменения и удаления данных структура данных предоставляет некоторый набор функций, составляющих интерфейс структуры данных. Структуры данных формируются с помощью типов данных, ссылок и операций над ними в выбранном языке программирования.
Массив — упорядоченный набор данных, для хранения данных одного типа, идентифицируемых с помощью одного или нескольких индексов. В простейшем случае массив имеет постоянную длину и хранит единицы данных одного и того же типа. Количество используемых индексов массива может быть различным. Массивы с одним индексом называют одномерными, с двумя — двумерными и т. д. Одномерный массив нестрого соответствует вектору в математике., двумерный — матрице. Чаще всего применяются массивы с одним или двумя индексами, реже — с тремя, ещё большее количество индексов встречается крайне редко.
Тип (сорт) — относительно устойчивая, независимая совокупность элементов, которую можно выделить во всем рассматриваемом множестве (предметной области> Типы данных бывзют следующие:
Перечислимый тип может хранить только те значения, которые прямо указаны в его описании:
-Числовые. Хранятся числа. Могут применяться обычные арифметические операции.
-Целочисленные: со знаком, то есть могут принимать как положительные, так и отрицательные значения; и без знака, то есть могут принимать только неотрицательные значения.
-Вещественные: с запятой (то есть хранятся знак и цифры целой и дробной частей) и с плавающей запятой (то есть число приводится к виду m*2е, где m — мантисса, е — экспонента, причем 1/2
— Числа произвольной точности, обращение с которыми происходит посредством длинной арифметики.
-Символьный тип. Хранит один символ. Могут использоваться различные кодировки.
-Логический тип. Имеет два значения: истина и ложь. Могут применяться логические операции. Используется в операторах ветвления и циклах. В некоторых языках является подтипом числового типа, при этом ложь=0, истина=1.
-Множество. В основном совпадает с обычным математическим понятием множества. Допустимы стандартные операции с множествами и проверка на принадлежность элемента множеству. В некоторых языках рассматривается как составной тип.
-Массив. Является индексированным набором элементов одного типа. Одномерный массив — вектор, двумерный массив — матрица.
-Строковый тип. Хранит строку символов. Аналогом сложения в строковой алгебре является конкатенация (прибавление одной строки в конец другой строки). В языках, близких к бинарному представлению данных, чаще рассматривается как массив символов, в языках более высокой абстракции зачастую выделяется в качестве простого.
-Запись (структура). Набор различных элементов (полей записи), хранимый как единое целое. Возможен доступ к отдельным полям записи. Например, struct в С или record в Pascal.
-Файловый тип. Хранит только однотипные значения, доступ к которым осуществляется только последовательно (файл с произвольным доступом, включённый в некоторые системы программирования, фактически является неявным массивом).
Теория алгоритмов — наука, изучающая общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. К задачам теории алгоритмов относятся формальное доказательство алгоритмической неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т. п.
Машина Тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). была предложена Аланом Тьюрингом в 1936_ходу для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
Устройство машины Тьюринга
В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара (ленточный символ — состояние), для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
Описание машины Тьюринга
Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита А, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj®qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква аj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурацииимеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.
Варианты машины Тьюринга
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Алгоритмические (или вычислительные) процессы обработки данных делятся на виды:
Линейным называется такой вычислительный процесс, в котором самостоятельные этапы вычислений выполняются в последовательности их записи, т.е. в естественном порядке.
Каждая операция является самостоятельной, независимой от каких-либо условий.
Линейные вычислительные процессы имеют место при вычислении арифметических выражений.
Ветвящимся называется такой процесс, в котором его реализация происходит по одному из нескольких заранее предусмотренных (возможных) направлений в зависимости от исходных условий или промежуточных результатов. Каждое отдельное направление вычислений в таком процессе называется ветвью вычисления. Выбор осуществляется проверкой выполнения логического условия.
В каждом конкретном случае обработки данных вычислительный процесс выполняется лишь по одной ветви, а выполнение остальных – исключается.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей- сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Направления ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» — условие выполнено, «нет» -условие не выполнено.
Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.
При реализации алгоритмов многих задач наблюдается многократное повторение отдельных этапов их вычислительного процесса. Такие многократно повторяемые этапы вычислений называются циклами, а вычислительные процессы, содержащие многократно повторяемые этапы называются циклическими.
Целью анализа трудоемкости алгоритмов является нахождение оптимального алгоритма для решения данной задачи. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функцией трудоемкости называется отношение, связывающие входные данные алгоритма с количеством элементарных операций.
Трудоёмкость алгоритмов по-разному зависит от входных данных. Для некоторых алгоритмов трудоемкость зависит только от объема данных, для других алгоритмов — от значений данных, в некоторых случаях порядок поступления данных может влиять на трудоемкость. Трудоёмкость многих алгоритмов может в той или иной мере зависеть от всех перечисленных выше факторов.
Одним из упрощенных видов анализа, используемых на практике, является асимптотический анализ алгоритмов. Целью асимптотического анализа является сравнение затрат времени и других ресурсов различными алгоритмами, предназначенными для решения одной и той же задачи, при больших объемах входных данных. Используемая в асимптотическом анализе оценка функции трудоёмкости, называемая сложностью алгоритма, позволяет определить, как быстро растет трудоёмкость алгоритма с увеличением объема данных. В асимптотическом анализе алгоритмов используются обозначения, принятые в математическом асимптотическом анализе.
[gl] Тема 6. Знакомство с языками программирования. [:]
Статьи к прочтению:
- Алгоритмизация и программирование
- Алгоритмы замещения страниц
Алгоритмы. Виды и свойства алгоритмов
Похожие статьи:
- Алгоритм. свойства алгоритмов. способы записи алгоритмов. базовые структуры алгоритмов. примеры. Алгоритм- это последовательность четких обозначенных предписаний, которые будучи применены к определенным имеющимся данным, обеспечиваю получение…
- Понятие алгоритма и его свойства В настоящее время понятие алгоритма — одно из фундаментальных понятий науки информатика. С одной стороны алгоритм является предметом изучения такой…
Источник: csaa.ru
Алгоритмы и программы
Теория алгоритмов, как наука, непосредственно связана с предметами математической логики и теории конечных автоматов. В Древней Греции Аристотель и его ученик Платон сформулировали основные правила логики, которые используются до нашего времени для доказательства правильности и решения логических задач.
Файлы: 1 файл
Глава 1. Алгоритмы и программы
1.1 История развития теории алгоритмов.
Теория алгоритмов, как наука, непосредственно связана с предметами математической логики и теории конечных автоматов. В Древней Греции Аристотель и его ученик Платон сформулировали основные правила логики, которые используются до нашего времени для доказательства правильности и решения логических задач.
Математическая логика – это наука о правилах формального логического мышления.
Теория автоматов изучает модели конечных автоматов, описывающие вычислительные узлы и элементы управления ЭВМ и других технических устройств.
Возникновение понятия «алгоритм» связано с именем узбекского математика Маххамада ибн Мусса Аль-Хорезми (IX в.), который сформулировал правила умножения и деления чисел в десятичной системе счисления. В латинских переводах с арабского языка его имя записывалось как algorismi. В дальнейшем термин алгоритм использовался для обозначения произвольных процессов, в которых искомые величины решаемых задач находятся последовательно из исходных данных по определённым правилам.
На протяжении многих веков учёные всего мира создали много методов и алгоритмов решения различных задач в математике и физике.
В 1936 году английский ученый Тьюринг разработал модель вычислительной машины для решения задач на основе алгоритмов и доказал:
- возможность автоматического решения задач с помощью алгоритмов, реализуемых в виде программы;
- реальность создания универсальных вычислительных машин.
На основе этой модели («машина Тьюринга») была построена классическая теория алгоритмов, основу которой составляли формальные описания следующих понятий:
2 – алгоритмический процесс;
3 – взаимосвязь между алгоритмом и алгоритмическим процессом и др.
Таким образом, само понятие алгоритма стало объектом математического изучения. В классической теории алгоритмов изучаются только вопросы существования или несуществования алгоритмов путем сведения этих вопросов к исследованию какого-либо одного узкого класса алгоритмов, что не позволяет охватить многие важные проблемы данной теории.
Теоретический аспект теории алгоритмов заключается в том, что она является фундаментов вычислительных наук, средством обоснования математики, доказательства правильности и разрешимости задач.
До середины XX века использовалось понятие алгорифма, заимствованное из математики. Позже с возникновением практического аспекта теории алгоритмов стал использоваться термин алгоритм. Причиной этому послужило развитие наук, изучающих структуру и принципы работы ЭВМ. Решение задач на ЭВМ было принято описывать в виде алгоритмов.
Создание компьютеров и языков программирования способствовало выделению теории алгоритмов как самостоятельной дисциплины. Сегодня понятие алгоритма вышло за пределы математики и используется в различных областях, где алгоритмом называют точно сформулированное правило, являющееся руководством для достижения необходимого результата. Кроме того, алгоритмы являются первоосновой для программирования задач на ЭВМ.
Практический аспект теории алгоритмов заключается в классификации задач по классам сложности, разработке алгоритмов решения трудных задач, оценке сложности алгоритмов, создании методов разработки быстрых эффективных алгоритмов. За последние годы было создано много хороших алгоритмов решения задач различных классов.
1.2 Основные понятия, определения и задачи теории алгоритмов.
Было выявлено, что если удается получить алгоритм решения какой-либо задачи, то эту задачу можно решать автоматически с помощью технических устройств.
Таким образом, алгоритмы являются:
- формой изложения научных результатов;
- руководством к действию при решении уже изученных проблем;
- средством автоматического решения задач;
- инструментом, используемым при исследовании и решении новых проблем;
- средством обоснования в математике;
- одним из средств описания сложных процессов.
Хотя алгоритмы важны для практики, практическая потребность не является первичной при изучении и разработке алгоритмов. Часто они разрабатываются для решения задач, которые не имеют пока практического применения. Однако многие научные результаты, полученные без практики, рано или поздно находят свое практическое применение.
1.2.1. Понятие алгоритма.
Существует два основных понятия алгоритма:
1 – интуитивное определение;
2 – формальное определение.
1. Алгоритм в интуитивном смысле – это точное предписание о выполнении в определенном порядке некоторой последовательности операций для решения всех задач некоторого заданного типа.
Содержание алгоритма, удобного для решения какой-либо задачи, позволяет использовать его даже человеку-непрофессионалу. Кроме того, его можно техническим устройством, выполняющим алгоритм автоматически (ЭВМ по заданной программе).
Формализация понятия алгоритма не должна учитывать ограниченность ресурсов, необходимых для его реализации, но требовать конечности этих ресурсов, т. е. возможной реализации как таковой.
2. Формальное определение алгоритма дается на основе математических методов и основывается либо на других понятиях, имеющих математическое определение, либо на понятиях-аксиомах, не требующих доказательства.
На основе свойств алгоритма можно сформулировать формальное определение. Алгоритм – это правило, сформулированное на некотором языке и определяющее процесс преобразования исходных данных в искомые результаты (алгоритмический процесс). При этом допустимые исходные данные представлены как предложения на языке исходных данных.
- понятностью для исполнителя;
- массовостью, то есть допустимостью для него всех предложений на языке описания исходных данных;
- детерминированностью и другими свойствами.
Неточность интуитивного понятия заключается в неточности тех терминов, через которые оно выражается, а именно:
смысл которых ясен, а научные
определения не составлены.
1.2.2 Алгоритмический процесс.
Алгоритмический процесс – это процесс последовательного преобразования конструктивных объектов, происходящий дискретно.
Конструктивные объекты – это слова, числа, предложения, которые описывают исходные данные, промежуточные результаты и конечные данные.
Алгоритмический процесс состоит из конечного числа шагов, каждый из которых является простым и выполняется за конечное время. Число шагов алгоритмического процесса связано с количеством времени S(t), затрачиваемого на их выполнение, а в ряде случаев и расходом других ресурсов.
1.2.3 Основные вопросы теории алгоритмов.
Основные вопросы теории алгоритмов можно сформулировать следующим образом:
- Что может делать ЭВМ.
- Каким образом ЭВМ решает задачи.
- Существует ли для заданной задачи эффективный алгоритм решения.
- Как сравнить различные алгоритмы решения одной и той же задачи.
1) Анализ вычислительных процессов, протекающих в соответствии с заданными алгоритмами, привел к следующему открытию. Было строго доказано существование таких типов задач, для которых невозможен единый эффективный метод решения, т. е. алгоритм, решающий все задачи данного класса (неразрешимые задачи).
Более того, ряд задач невозможно решить на современном уровне развития ЭВМ (задачи искусственного интеллекта). Поэтому одной из главных целей теории алгоритмов является исследование различных типов задач по областям применения с целью выяснить, возможен ли для них алгоритм решения.
2) Ответ на второй вопрос требует рассмотрения принципов работы ЭВМ и организации вычислительных процессов для различных структур ЭВМ в рамках их классификации, а также оценки качества алгоритмов, реализуемых в различных ЭВМ.
3) Эффективным считается алгоритм, обладающий наибольшим быстродействием.
4) Для сравнения различных алгоритмов по быстродействию необходимо рассмотреть следующие параметры:
- временная функция T(N);
- функция сложности алгоритма O(g(N)), учитывающая зависимость скорости роста числа шагов алгоритма от объема исходных данных.
1.3 Алгоритмы и языки.
Как уже отмечалось, алгоритм – это правило, а любое правило должно быть четко сформулировано на каком-либо языке (1). Это возможно лишь при условии, что исходные данные и искомые результаты могут быть описаны в полном объеме на каком-либо другом языке (2). Т. е. каждому исходному данному, промежуточному и конечному результатам соответствует некоторое предложение на этом языке. Смысл предложения должен быть однозначным.
Язык (1) – это язык описания алгоритмов (алгоритмический язык).
Язык (2) – это язык описания данных (язык операндов).
В самом алгоритме присутствуют не конкретные исходные, промежуточные или конечные данные, а только их названия (например, переменные в программах). Для задания алгоритмического процесса достаточно знать названия операций, их порядок и названия искомых результатов.
Операнд – это объект, над которым выполняется операция, задаваемая алгоритмом. Все предложения языка операндов считаются допустимыми, а какие-либо сочетания символов (алфавита), не принадлежащих данному языку, по определению недопустимы.
Разнообразие допустимых предложений языка операндов описывает разнообразие предметов и задач, что определяет свойство массовости алгоритма.
1.4. Способы записи алгоритмов
Существуют различные формы ( способы) представления алгоритмов. Основными среди них являются:
- Словесное описание алгоритма на естественном языке (вербальная форма).
- Построчная запись алгоритма (более строгое описание на естественном языке).
- Представление алгоритма в виде блок-схемы.
- Способ изображения алгоритма с помощью структурограммы (схема Насси-Шнейдермана).
- Запись алгоритма на каком-либо языке программирования.
Пример: Найти наибольший общий делитель (НОД) двух целых положительных чисел методом последовательного вычитания (алгоритм Евклида).
Вербальное представление алгоритма.
«Чтобы найти НОД двух целых положительных чисел составим таблицу из двух столбцов и назовем их m и n. Запишем первое из заданных чисел в столбец m, а второе — в столбец n. Если данные числа не равны, заменим большее из них результатом вычитания из большего меньшего числа. Повторяем такие замены до тех пор, пока числа не окажутся равными, после чего число из столбца m считаем искомым результатом». Очевидно, такая форма представления алгоритма может тяжело восприниматься читателем и применяется в основном при решении простых задач.
Построчная запись алгоритма.
- Начало.
- Ввод m, n.
- Если m ¹ n, перейти к пункту 4, иначе — к пункту 7.
- Если m > n, перейти к пункту 5, иначе — к пункту 6.
- m=m-n; перейти к пункту 3.
- n=n-m; перейти к пункту 3.
- НОД=m.
- Вывод результата.
- Конец.
Источник: www.yaneuch.ru