Алгоритм диффи хеллмана программа

Давно хотел опубликовать статью тут, но никак не находил повода для хорошей темы. Однако я уже давно веду телеграм канал по Backend разработке, в котором публикую разную информацию о Backend, рассказываю про технологии и делюсь полезным контентом.

Сегодня я хочу рассказать вам о волшебном алгоритме, который стоит за безопасным общением в интернете, и, в частности, в нашем любимом мессенджере — Telegram. Этот алгоритм называется алгоритмом Диффи-Хеллмана, и его история начинается в далеком 1976 году. На этом с историей закончим

Как это работает?

Алгоритм Диффи-Хеллмана используется для того, чтобы две стороны могли создать общий секретный ключ, его еще называют «транспортный ключ», который затем используется для шифрования и дешифрования сообщений.

❗️Самое главное — этот ключ создается без прямого обмена им между сторонами.

Принцип работы

Алгоритм основан на принципе «сложности вычисления дискретного логарифма».

Звучит страшно, но суть в том, что существуют математические функции, которые легко вычислить в одну сторону, но очень сложно обратно. Например если обратная операция сложения это вычитание, а для умножения это деление, то вот для операции остатка от деления обратной операции нет. Поэтому для алгоритма Диффи-Хеллмана используются такие функции.

Шифрование Диффи-Хеллман. Шифрование в телеграмм

Пример создания секретного ключа

Допустим, Алиса и Боб хотят создать общий секретный ключ, используя алгоритм Диффи-Хеллмана. Они выполняют следующие шаги:

1. Алиса и Боб выбирают общие параметры: основаниеg (допустим, 5) и большое простое числоp (допустим, 23).
2. Алиса генерирует свой секретный ключ a (допустим, 6) и вычисляет свой публичный ключ A: A = g^a mod p = 5^6 mod 23 = 15625 mod 23 = 8.
3. Боб генерирует свой секретный ключ b (допустим, 9) и вычисляет свой публичный ключ B: B = g^b mod p = 5^9 mod 23 = 1953125 mod 23 = 11.
4. Алиса и Боб обмениваются публичными ключами: Алиса отправляет свой ключ A (8) Бобу, а Боб отправляет свой ключ B (11) Алисе.
5. Алиса вычисляет общий секретный ключ s: s = B^a mod p = 11^6 mod 23 = 1771561 mod 23 = 9.
6. Боб вычисляет общий секретный ключ s: s = A^b mod p = 8^9 mod 23 = 134217728 mod 23 = 9.

Теперь Алиса и Боб имеют общий секретный ключ s, который равен 9. Этот ключ может быть использован для дальнейшего зашифрования и расшифрования сообщений между ними.

Безопасность общения

Теперь, когда стороны имеют один и тот же секретный ключ, они могут использовать его для шифрования и дешифрования сообщений. На протяжении всего процесса прямой обмен секретными данными не происходит, что делает метод безопасным для общения.

Применение Diffie-Hellman алгоритма

Алгоритм Diffie-Hellman используется во множестве криптографических протоколов и стандартов, таких как:

1. TLS/SSL: Протоколы передачи данных, обеспечивающие защищенное соединение между клиентом и сервером.

2. IPSec: Протокол безопасности для защиты данных, передаваемых через сети, в том числе в VPN-соединениях.

Алгоритм Диффи-Хеллмана

3. SSH: Протокол безопасной оболочки, используемый для безопасного удаленного доступа к серверам и обмена данными между ними.

Реализация на GoLang

А теперь непосредственно расскажу как я это реализовал, весь код представлен в этом репозитории: https://github.com/vseriousv/diffiehellman.

Начнем с того что я буду использовать Go-Ethereum для генерации приватных и публичных ключей. Такой пакет я уже написал ранее, его можно посмотреть в этом репозитории: https://github.com/vseriousv/blockchainkeys.

Там все просто, импортируем библиотеку и вызываем функцию NewBlockchain() , в которую нужно передать тип блокчейна blockchainkeys.Ethereum . Получаем структуру, у которой можем вызвать метод GenerateKeyPair(). Получим приватный и публичный ключи.

// Пример функции, которая возвращает пару приватного и публичного ключа func getKeys() (string, string, error) < bc, err := blockchainkeys.NewBlockchain(blockchainkeys.Ethereum) if err != nil < fmt.Println(«Error:», err) return «», «», err >privateKey, publicKey, _, err := bc.GenerateKeyPair() if err != nil < fmt.Println(«Error:», err) return «», «», err >return privateKey, publicKey, nil >

Сгенерируем пару ключей для Алисы и Боба используя нашу функцию:

// Generation ALisa pair privateAlisa, publicAlisa, err := getKeys() if err != nil < log.Fatal(err) >// Generation Bob pair privateBob, publicBob, err := getKeys() if err != nil

Для того чтобы получить транспортный ключ, напишем функцию, которая принимает на вход публичный ключ собеседника и наш приватный ключ.

func GetTransportKey(publicKey, privateKey string) (string, error) < // Так как ключи в Ethereum имеют прфик 0x, обрезаем его privateKeyAHex := privateKey[2:] // Приводим приватный ключ к BigInt privateKeyABigInt, success := new(big.Int).SetString(privateKeyAHex, 16) if !success < return «», errors.New(«invalid private key format») >// Тут тоже обрезаем префикс publicKeyBHex := publicKey[2:] // Приводим в байтовый формат publicKeyBBytes, err := hex.DecodeString(publicKeyBHex) if err != nil < return «», errors.New(«invalid public key format») >// Далее нам нужно конвертировать байтовый формат в secp256k1 publicKeyB, err := crypto.UnmarshalPubkey(publicKeyBBytes) if err != nil < return «», errors.New(«unmarshalling public key failed») >// магическая функция, которая возвращает нам X и Y координаты элиптической кривой согласно спецификации secp256k1 sharedSecretX, _ := secp256k1.S256().ScalarMult(publicKeyB.X, publicKeyB.Y, privateKeyABigInt.Bytes()) if sharedSecretX == nil < return «», errors.New(«scalar multiplication failed») >// Ну и заветная функция возвращающая нам транспортный ключ transportKey := crypto.Keccak256(sharedSecretX.Bytes()) return hex.EncodeToString(transportKey), nil >
Hidden text

Я дико извиняюсь, что приходится очень поверхностно описывать процедуры работы с элиптическими кривыми и как устроены алгоритмы криптографии в блокчейне, посколько иначе эта статья превратиться в длиннопост. Однако в будущем я попробую написать статью про спецификацию secp256k1.

Для того чтобы зашифровать сообщение я написал простые функции с использованием стандартной библиотеки «crypto» в Go. https://pkg.go.dev/crypto/aes

func Encrypt(message, key []byte) ([]byte, error) < // Create a new AES block cipher block, err := aes.NewCipher(key[:32]) if err != nil < return nil, err >// Create a new GCM encryption mode aead, err := cipher.NewGCM(block) if err != nil < return nil, err >// Create a random nonce nonce := make([]byte, aead.NonceSize()) if _, err := rand.Read(nonce); err != nil < return nil, err >// Encrypt the message using a nonce and propagate the tag ciphertext := aead.Seal(nil, nonce, message, nil) ciphertext = append(nonce, ciphertext. ) return ciphertext, nil > func Decrypt(cipherText, key []byte) (string, error) < // Create a new AES block cipher block, err := aes.NewCipher(key[:32]) if err != nil < return «», err >// Create a new GCM encryption mode aead, err := cipher.NewGCM(block) if err != nil < return «», err >// Extract the nonce from the encrypted message nonceSize := aead.NonceSize() nonce, ciphertext := cipherText[:nonceSize], cipherText[nonceSize:] // Decode the message and check the tag plaintext, err := aead.Open(nil, nonce, ciphertext, nil) if err != nil < return «», nil >return string(plaintext), nil >

Итого имеем, что у Алисы и Боба есть пары ключей и мы теперь можем получить транспортный ключ для Алисы, используя ее приватный ключ и публичный ключ Боба, воспользовавшись нашей функцией GetTransportKey(publicBob, privateAlisa) :

// Get transportKey for Alisa, // Alisa has publicKey(Bob) and privateKey(Alisa) transportKeyOne, err := transport_key.GetTransportKey(publicBob, privateAlisa) if err != nil < log.Fatal(err) >log.Println(«transportKeyOne», transportKeyOne)

А далее зашифруем наше сообщение полученным транспортным ключом:

// Alisa’s encryption message for Bob message := []byte(«Hello Bob, I’m Alisa») encryptionMessage, err := encryption.Encrypt(message, []byte(transportKeyOne)) if err != nil

Чтобы Бобу расшифровать данное сообщение, ему требуется получить транспортный ключ используя свой приватный ключ и публичный ключ Алисы, используя нашу функцию GetTransportKey(publicAlisa, privateBob)

// Get transportKey for Bob, // Bob has publicKey(Alisa) and privateKey(Bob) transportKeyTwo, err := transport_key.GetTransportKey(publicAlisa, privateBob) if err != nil < log.Fatal(err) >log.Println(«transportKeyTwo», transportKeyTwo)

А далее расшифровать сообщение используя наш транспортный ключ Боба:

// Bob decrypt message from Alisa messageResult, err := encryption.Decrypt(encryptionMessage, []byte(transportKeyTwo)) if err != nil

В итоге выведем эти сообщения в лог, убедимся, что все работает.

Всем спасибо за внимание.

Источник: habr.com

Алгоритм Диффи-Хеллмана: обзор и реализация на C

Алгоритм Диффи-Хеллмана используется для установления общего секрета между двумя сторонами, который можно использовать для секретной связи для обмена данными в общедоступной сети.

Графическое объяснение:

Процесс начинается с того, что две стороны, Алиса и Боб, договариваются о произвольном начальном цвете, который не нужно держать в секрете (но он должен каждый раз быть другим); в этом примере цвет желтый. Каждый из них выбирает секретный цвет — красный и голубой соответственно, — который они держат при себе. Важнейшая часть процесса заключается в том, что Алиса и Боб теперь смешивают свой секретный цвет с их общим цветом, в результате чего получается смесь оранжевого и синего соответственно, а затем публично обмениваются двумя смешанными цветами. Наконец, каждый из двоих смешивает цвет, полученный от партнера, со своим собственным цветом. В результате получается окончательная цветовая смесь (коричневый), идентичная цветовой смеси партнера.

Ева-подслушиватель не сможет определить общий секретный цвет.

Криптографическое объяснение:

Алгоритм сам по себе очень прост. Предположим, что Алиса хочет установить общий секрет с Бобом. Вот пример протокола с секретными значениями в red .

1. Алиса и Боб соглашаются использовать простое число п = 23 и основание грамм = 5. (Эти два значения выбраны таким образом, чтобы гарантировать, что результирующий общий секрет может принимать любое значение от 1 до п–1).
2. Алиса выбирает секретное число а = 6 , затем отправляет Бобу А = грамм а мод п (А = 5 6 мод 23 = 8)
3. Боб выбирает секретное целое число б = 15 , затем отправляет Алисе Б = грамм б мод п (Б = 5 15 мод 23 = 19)
4. Алиса вычисляет с = Б а мод п ( с = 19 6 мод 23 = 2 )
5. Боб вычисляет с = А б мод п ( с = 8 15 мод 23 = 2 )
6. Алиса и Боб теперь имеют общий секрет (число 2 ).

Число, которое Алиса получила на шаге 4, совпадает с числом, полученным Бобом на шаге 5.

A b mod p = (g a mod p) b mod p = g ab mod p
B a mod p = (g b mod p) a mod p = g ba mod p

Алгоритм Диффи-Хеллмана в основном используется для обмена криптографическими ключами для использования в алгоритмах симметричного шифрования, таких как AES. Обратите внимание, что информация не передается во время обмена ключами. Здесь две стороны вместе создают ключ.

Реализация:

Источник: www.techiedelight.com

Как работает обмен ключами в протоколе Диффи-Хеллмана

Обмен ключами с помощью протокола Диффи-Хеллмана (DH) — это метод безопасного обмена криптографическими ключами по общедоступному каналу. Это один из первых протоколов с открытым ключом, который изначально был концептуализирован Ральфом Мерклем и назван в честь Уитфилда Диффи и Мартина Хеллмана. DH является одним из первых практических примеров обмена открытыми ключами. Сегодня DH используется для многих приложений, таких как, например, Proton Mail, SSH, GPG и так далее. В статье мы рассмотрим принципы работы этого протокола и проблемы, которые он решает.

Проблема в сквозном шифровании

Давайте возьмём простейшую ситуацию. Представьте, Майкл и я решили обменяться информацией. А хакер по имени Мистер Робот пытается перехватить наше сообщение.

Логичный способ помешать Мистеру Роботу прочитать наше сообщение — шифрование. Предполагается, что даже если способ шифрования известен, сообщение не может быть расшифровано без ключа. Поэтому, пока мы с Майклом используем один и тот же метод шифрования и одинаковый ключ, мы можем общаться конфиденциально! Однако есть одна проблема…

Чтобы расшифровать сообщение Майкла, мне нужно, чтобы он отправил мне ключ по сети. Проблема в том, что Мистер Робот следит за перепиской и обязательно увидит ключ. Получив ключ, он легко сможет расшифровать все наши сообщения! Эта проблема обмена ключами решается с помощью алгоритма Диффи-Хеллмана.

Основы криптографии: от математики до физики

Как Диффи-Хеллман решает проблему?

Диффи-Хеллман работает по принципу неполного обмена ключом шифрования по сети. У каждой стороны есть открытый ключ (который может видеть каждый, включая Мистера Робота) и закрытый ключ (его может видеть только пользователь компьютера). У меня нет доступа к личному ключу Майкла. У Майкла — к моему.

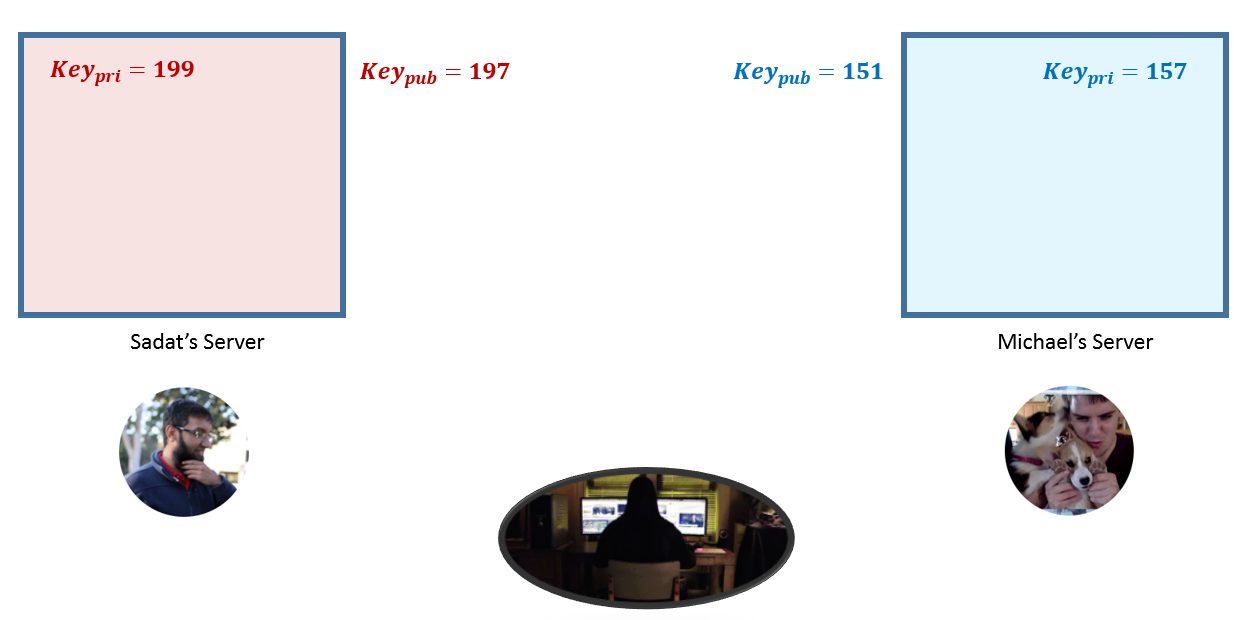
Теперь давайте предположим, что мы оба используем общий алгоритм шифрования, и нам нужно каким-то образом восстановить общий ключ шифрования, не передавая слишком много информации через сеть.

Создание базового класса

Ниже приведён предварительный базовый класс одной стороны, использующей шифрование DH. Пока не беспокойтесь о деталях, так как мы подробно рассмотрим каждую функцию!

class DH_Endpoint(): def __init__(self, public_key1, public_key2, private_key): self.public_key1 = public_key1 self.public_key2 = public_key2 self.private_key = private_key self.full_key = None def generate_partial_key(self): partial_key = self.public_key1 ** self.private_key partial_key = partial_key % self.public_key2 return partial_key def generate_full_key(self, partial_key_r): full_key = partial_key_r ** self.private_key full_key = full_key % self.public_key2 self.full_key = full_key return full_key def encrypt_message(self, message): encrypted_message = «» key = self.full_key for c in message: encrypted_message += chr(ord(c) + key) return encrypted_message def decrypt_message(self, encrypted_message): decrypted_message = «» key = self.full_key for c in encrypted_message: decrypted_message += chr(ord(c) — key) return decrypted_message

Давайте определим секретное сообщение, которое Майкл планирует отправить мне, а также наши закрытые и открытые ключи, установленные на компьютерах. В реальной жизни обычно используются большие простые числа, здесь мы будем использовать небольшие значения для простого отображения математической части.

message = «This is a very secret message. » s_public = 197 s_private = 199 m_public = 151 m_private = 157 Sadat = DH_Endpoint(s_public, m_public, s_private) Michael = DH_Endpoint(s_public, m_public, m_private)

Частичный обмен ключами

Давайте предположим, что мы ничего не видим внутри сервера Майкла (включая его личный ключ).

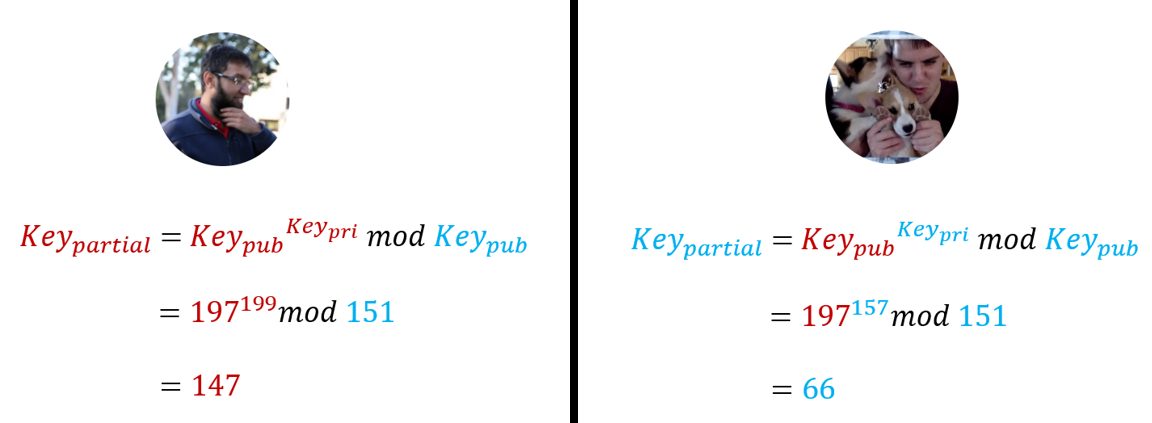
Теперь мне нужно создать частичный ключ шифрования, используя 3 доступные единицы информации: мой закрытый и открытый ключи и открытый ключ Майкла. Алгоритмически мы согласились использовать мой открытый ключ в качестве базы и его открытый ключ в качестве модуля.

Если мы посмотрим на нашу функцию для генерации частичного ключа, то она именно эти вычисления и делает:

def generate_partial_key(self): partial_key = self.public_key1 ** self.private_key partial_key = partial_key % self.public_key2 return partial_key

Теперь давайте сгенерируем этот частичный ключ и отправим его Майклу по сети.

s_partial = Sadat.generate_partial_key() print(s_partial) # 147

Таким же образом Майкл посылает мне свой частичный ключ по сети.

m_partial = Michael.generate_partial_key() print(m_partial) # 66

Сравнение обоих вычислений частичного ключа:

Мистер Робот, естественно, увидел обмен частичными ключами. Он также знает оба открытых ключа. Теперь ему нужно взломать наши соответствующие закрытые ключи.

Всё, что знает Мистер Робот, — это частичные ключи и соответствующие открытые ключи, а также формула, используемая для получения частичных ключей. Особенность вычисления по модулю в том, что функция заставляет значение циклически изменяться. Если у вас есть модуль 151 , значение будет между 0 и 151-1 .

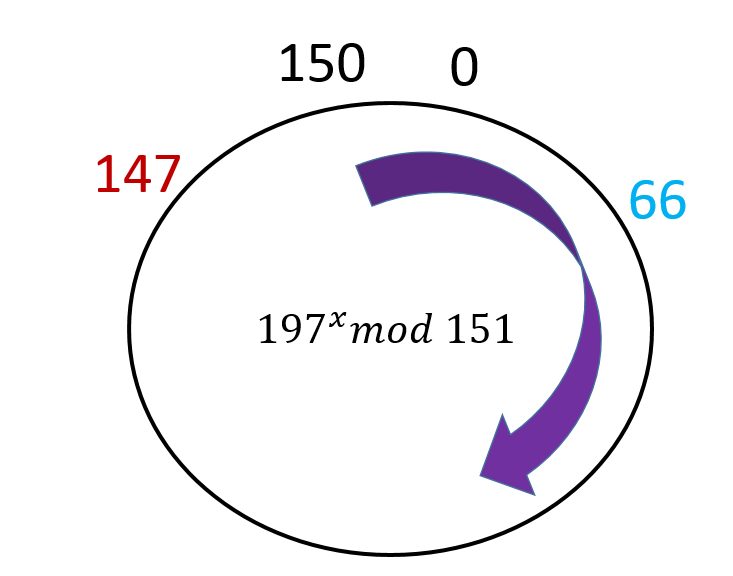
Существует бесконечное число возможных значений, которые по модулю 151 будут равны либо 66 , либо 147 . В результате информации для получения закрытых ключей пользователей недостаточно (если не считать грубый перебор безумно большого числа всевозможных вариантов). Кроме того, в примере используются небольшие числа для закрытых и открытых ключей, что делает подбор реальным. В реальной жизни это было бы почти невозможно!

Генерация полного ключа

Теперь, когда мы успешно обменялись частичными ключами, давайте снова применим операторы степени и деления с остатком к частичному ключу другого человека, используя наши собственные закрытые ключи следующим образом:

Реализация этого в Python:

def generate_full_key(self, partial_key_r): full_key = partial_key_r ** self.private_key full_key = full_key % self.public_key2 self.full_key = full_key return full_key

Код с моей стороны:

s_full = Sadat.generate_full_key(m_partial) print(s_full) # 75

И то же самое для Майкла, использующего мой частичный ключ:

m_full=Michael.generate_full_key(s_partial) print(m_full) # 75

Заметили что-нибудь интересное? Мы оба получили одинаковые полные ключи, равные 75 ! Причина заключается в следующем математическом соотношении:

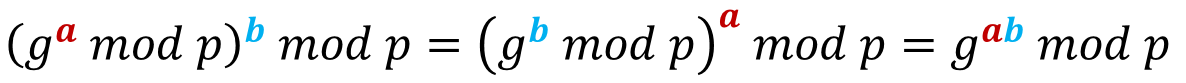
Здесь a и b — закрытые ключи, а g и p — открытые. Нам удалось обменяться друг с другом по сети достаточным количеством информации, чтобы сгенерировать общий ключ шифрования, не ставя под угрозу наши закрытые ключи.

Время шифрования!

Теперь, когда у нас есть общий ключ шифрования, пришло время начать обмен сообщениями! Как объяснялось в начале этого раздела, Майкл хочет отправить мне зашифрованное сообщение. Вот простой алгоритм, который я написал для шифрования сообщения Майкла:

def encrypt_message(self, message): encrypted_message = «» key = self.full_key for c in message: encrypted_message += chr(ord(c) + key) return encrypted_message

Ничего особенного. Каждый символ кодируется в целое число, значение ключа добавляется, а затем целое число преобразуется обратно в символ. Этот процесс повторяется для каждого символа в сообщении.

Первоначальное сообщение, которым хотел поделиться Майкл: «This is a very secret message. ». Давайте добавим его в алгоритм с нашим новым ключом шифрования.

Прим. пер.: это шифр простой замены, которым в реальной жизни пользоваться не стоит. Взламывается чуть сложнее классического, но всё равно достаточно быстро.

m_encrypted = Michael.encrypt_message(message) print(m_encrypted) # ‘x9f³´¾k´¾k¬kÁ°½Äk¾°®½°¿k¸°¾¾¬²°lll’

Зашифрованное сообщение — « x9f³´¾k´¾k¬kÁ°½Äk¾°®½°¿k¸°¾¾¬²°lll », что при чтении выглядит как бессвязный набор символов. Мистер Робот понятия не имеет, чем Майкл делится со мной по сети.

Теперь пришло время расшифровать сообщение с моей стороны.

def decrypt_message(self, encrypted_message): decrypted_message = «» key = self.full_key for c in encrypted_message: decrypted_message += chr(ord(c) — key) return decrypted_message

Эта функция делает обратное преобразование. На этапе шифрования было добавлено значение ключа, на этапе расшифровки будет вычтено то же самое значение.

message = Sadat.decrypt_message(m_encrypted) print(message) # ‘This is a very secret message. ‘

Получил сообщение! Хорошая попытка, Мистер Робот. Нам удалось обмениваться зашифрованными сообщениями, не поставив под угрозу наши ключи шифрования.

Заместитель руководителя службы мониторинга и реагирования на инциденты (киберб безопасность) Открытие , , можно удалённо , По итогам собеседования