6 в чем заключается оценка надежности программ

Надежность программного обеспечения гораздо важнее других его характеристик, например, времени исполнения, и хотя абсолютная надежность современного программного обеспечения, по-видимому, недостижима, до сих пор не существует общепринятой меры надежности компьютерных программ. В статье анализируются причины создавшегося положения и предлагается подход к решению проблемы. Обоснование проблемы Причины сложившейся ситуации Вероятностный подход к проблеме надежности Компьютерная программа как объект исследования Надежность и правильность программы Модель последовательности испытаний Бернулли Некоторые следствия Заключение Литература Надежность программного обеспечения

Надежность программного обеспечения гораздо важнее других его характеристик, например, времени исполнения, и хотя абсолютная надежность современного программного обеспечения, по-видимому, недостижима, до сих пор не существует общепринятой меры надежности компьютерных программ. В статье анализируются причины создавшегося положения и предлагается подход к решению проблемы.

Тургенбаев Д.Н. — 44.НАДЕЖНОСТЬ ОПЕРАТОРА И ЭКСПЛУАТАЦИОННАЯ НАДЕЖНОСТЬ СИСТЕМ

Обоснование проблемы

Проблема надежности программного обеспечения относится, похоже, к категории «вечных». В посвященной ей монографии Г.Майерса [1], выпущенной в 1980 году (американское издание — в 1976), отмечается, что, хотя этот вопрос рассматривался еще на заре применения вычислительных машин, в 1952 году, он не потерял актуальности до настоящего времени.

Отношение к проблеме довольно выразительно сформулировано в книге Р.Гласса ([2]): «Надежность программного обеспечения — беспризорное дитя вычислительной техники». Следует далее отметить, что сама проблема надежности программного обеспечения имеет, по крайней мере, два аспекта: обеспечение и оценка (измерение) надежности. Практически вся имеющаяся литература на эту тему, включая упомянутые выше монографии, посвящена первому аспекту, а вопрос оценки надежности компьютерных программ оказывается еще более «беспризорным». Вместе с тем очевидно, что надежность программы гораздо важнее таких традиционных ее характеристик, как время исполнения или требуемый объем оперативной памяти, однако никакой общепринятой количественной меры надежности программ до сих пор не существует.

Для обеспечения надежности программ предложено множество подходов, включая организационные методы разработки, различные технологии и технологические программные средства, что требует, очевидно, привлечения значительных ресурсов. Однако отсутствие общепризнанных критериев надежности не позволяет ответить на вопрос, насколько надежнее становится программное обеспечение при соблюдении предлагаемых процедур и технологий и в какой степени оправданы затраты. Таким образом, приоритет задачи оценки надежности должен быть выше приоритета задачи ее обеспечения, чего на самом деле не наблюдается.

Причины сложившейся ситуации

Судя по имеющимся публикациям, вопрос обеспечения надежности программ считается более важным, чем вопрос ее оценки. Ситуация выглядит парадоксальной: совершенно очевидно, что прежде, чем улучшать какую-то характеритику, следует научиться ее измерять, и уж, по крайней мере, необходимо иметь единицу измерения.

Лекция 9: Принципы обеспечения качества программных средств

Основная причина такого положения коренится в том, что источником ненадежности программ служат содержащиеся в них ошибки, и если ошибки отсутствуют, то программа абсолютно надежна. По существу, все меры по обеспечению надежности программ направлены на то, чтобы свести к минимуму (если не искючить вообще) ошибки при разработке и как можно раньше их выявить и устранить после изготовления программы. Следует заметить, что безошибочные программы, конечно же, существуют, однако современные программые системы слишком велики и почти неизбежно содержат ошибки. Хотя это обстоятельство отмечается многими авторами и известно любому программисту-практику, существует, по-видимому, некий психологический барьер, не позволяющий признать факт наличия ошибок в программном обеспечении неизбежной реальностью: поскольку не существует точного критерия, позволяющего определить максимальный размер свободной от ошибок программы, всегда остается надежда, что в данной конкретной программной системе их не осталось.

Имеется еще одно обстоятельство психологического характера. Как известно, вопрос надежности для аппаратуры хорошо разработан. Источником ненадежности аппаратуры служат объективные факторы, неподвластные человеку (скачки напряжения питания, альфа-частицы и т.д.), поэтому человечество давно смирилось с мыслью о том, что абсолютно надежной аппаратуры не бывает и можно говорить лишь о степени надежности, выражаемой в каких-то единицах (например, среднее время между двумя последовательными отказами). Источник же ненадежности программ ошибки, которые делают люди, их создающие и использующие, поэтому кажется, что проблема лишь в том, чтобы заставить (или научить) их работать «правильно».

Третья причина состоит в том, что проблему выбора единицы измерения надежности компьютерной программы невозможно решить в рамках промышленного подхода, который в настоящее время занимает в программированиии все более доминирующее положение. Наиболее характерный пример — использование, по аналогий с аппаратурой, в качестве меры надежности программы среднего времени между двумя последовательными ошибочными срабатываниями. Рассуждения в обоснование аналогий такого рода В.Турский ([3]) довольно резко охарактеризовал как наукообразные; сама же характеристика плохо отражает суть дела и не получила широкого признания.

Метод аналогий, конечно, универсален, однако не следует забывать, что любая аналогия имеет границы применимости. В данном случае, поскольку речь идет о фундаментальном понятии (единице измерения), следует не просто переносить характеристики надежности аппаратуры на программы, а воспользоваться более фундаментальными аналогиями.

Вероятностный подход к проблеме надежности

Прежде всего полезно напомнить, откуда берутся характеристики надежности аппаратуры. Надежность, в конечном счете, — понятие статистическое, т.е. предполагается наличие некоторого (достаточно большого) количества одинаковых образцов, испытаний и т.д. Существенно также, что имеется элемент случайности.

Изучению случайных явлений посвящен специальный раздел математики: теория вероятностей. Основное понятие этой теории — пространство элементарных событий (выборочное пространство, пространство исходов), на котором задается некоторая (вероятностная) мера. Случайная величина, согласно теории, есть функция, заданная на пространстве элементарных событий. Наконец, в качестве меры надежности используются некоторые характеристики случайной величины (как правило, математическое ожидание).

Таким образом, последовательный вероятностный подход при изучении надежности состоит в анализе исследуемого объекта (самолета, системы охраны, компьютерной программы и т.д.), построении, исходя из «физических» соображений о его природе, пространств элементарных событий, введении на них вероятностной меры и рассмотрении случайных величин.

К сожалению, первый этап исследований — анализ объекта и построение пространств элементарных событий — обычно опускают и сразу переходят к рассмотрению случайных величин, упуская из вида, что случайная величина есть на самом деле функция, заданная на пространстве элементарных событий.

Компьютерная программа как объект исследования

Прежде чем говорить о надежности объекта, следует уточнить, что подразумевается под объектом. Как известно, компьютерная программа имеет несколько разных форм (или представлений): внешние спецификации, исходный текст, исполняемый код и т.д. Общепринятая точка зрения состоит в том, что программа представляет собой объект, инвариантный относительно форм его представления. Согласно этой точке зрения, внешние спецификации, исходные тексты на языках разных уровней, а также исполняемые коды для разных процессоров есть разные формы представления одной и той же программы. Указанная точка зрения полезна при разработке программного обеспечения, поскольку позволяет выявить наиболее существенные для приложения свойства программы, общие для всех ее представлений, однако она малопродуктивна, если речь идет, например, о такой количественной характеристике, как время исполнения: ясно, что указанная характеристика относится лишь к одной из форм представления — исполняемомому коду и, кроме того, зависит не только от программы, но и от типа процессора.

На интуитивном уровне понятие надежности программы отражает тот факт, что она не всегда может давать правильный результат. Это означает, что надежность программы является характеристикой ее исполняемого кода. Исполняемый код соотносится с исходным текстом так же, как, например, электродвигатель и его чертежи: можно говорить о надежности изготовленного изделия, но бессмысленно говорить о надежности описания, чертежа, текста. Две функционально идентичные программы, написанные на разных языках, или подготовленные для разных типов машин, или для одной и той же машины, но с использованием разных компиляторов, с точки зрения надежности следует считать разными.

Надежность и правильность программы

Программа считается правильной, если она не содержит ошибок. Такая программа не дает неверных результатов, т.е. она абсолютно надежна. Этот факт породил ложное представление о том, что число ошибок в программе можно считать наиболее естественной мерой надежности ([1]). Было выполнено довольно много работ, в которых предлагались различные методы оценки числа оставшихся в программе ошибок по результатам ее тестирования, в том числе метод «засорения» известными ошибками, однако, как показывают приводимые ниже соображения, количество ошибок в программе не имеет никакого отношения к ее надежности:

1. Число ошибок в программе — величина «ненаблюдаемая», наблюдаются не сами ошибки, а результат их проявления.

2. Неверное срабатывание программы может быть следствием не одной, а сразу нескольких ошибок.

3. Ошибки могут компенсировать друг друга, так что после исправления какой-то одной ошибки программа может начать «работать хуже».

4. Надежность характеризует частоту проявления ошибок, но не их количество; в то же время хорошо известно, что ошибки проявляются с разной частотой: некоторые ошибки остаются невыявленными после многих месяцев и даже лет эксплуатации, но, с другой стороны, нетрудно привести примеры, когда одна единственная ошибка приводит к неверному срабатыванию программы при любых исходных данных, т.е. к нулевой надежности.

Следует также отметить, что если число ошибок рассматривать как меру надежности, то в терминологии теории вероятностей это число есть случайная величина, однако самый главный вопрос — на каком пространстве элементарных событий она задана — нигде не затрагивался.

Наконец, важно подчеркнуть, что, с точки зрения надежности, в результате исправления ошибки или любой другой коррекции получается новая программа с другим, чем до коррекции, показателем надежности.

Таким образом, число ошибок в программе характеризует скорее не программу, а ее изготовителей и используемый инструментарий.

Модель последовательности испытаний Бернулли

Рассмотрим для простоты класс программ, имеющих единственный вход и выход, т.е. не содержащих бесконечных циклов. Фазу выполнения программы от начала до завершения будем называть запуском. Все возможные результаты запуска разобьем на два класса: правильные и неправильные (ошибочные).

Будем считать, что любой результат всегда можно отнести к одному из этих классов. (Ясно, что по этому вопросу возможны разногласия между изготовителями программы и пользователями, однако будем предполагать, что имеется какой-то общий критерий, например, «клиент всегда прав».) Рассмотрим классическую вероятностную модель последовательности испытаний Бернулли. Пространство элементарных событий в этой модели содержит 2 n точек, где n — число испытаний (в данном случае под испытанием подразумевается запуск программы). Каждый запуск программы имеет два исхода: правильный и неправильный. Обозначим вероятность неправильного исхода р, а вероятность правильного — (1-p). Вероятность того, что из n запусков К приведут к неправильному результату, выражается хорошо известной формулой биномиального распределения ([4]).

B(р,n,k) = C(n,k) * pk * (1-р)(n-k), (1)

где С(n,k) — число сочетаний. Вероятность р априори неизвестна, но по результатам запусков известны n и k. Величина В как функция р имеет максимум при

р = k/n. (2)

В качестве меры надежности программы можно принять величину

R = 1 — k/n = (n-k)/n, (3)

значения которой (от 0 до 1) согласуются с общепринятым смыслом термина надежность: например, если все запуски окончились с ошибочным результатом (k = n), то надежность — нулевая.

Наиболее существенное предположение в данной модели состоит в том, что запуски программы считаются независимыми. Это означает, что результаты предыдущих запусков не дают никакой информации о результатах следующего. Ясно, что это предположение на практике выполняется не всегда: например, повторный запуск с теми же входными данными даст, очевидно, тот же самый результат. *

Следует отметить, что изготовитель программы и ее пользователь располагают разной информацией о ней. Например, изготовителю заведомо известна логика программы, так что по результатам запуска с некоторыми исходными данными он иногда может точно предсказать результаты запусков с другими исходными данными (на этом, в конечном счете, основана любая методика тестирования), и в этом смысле предположение о независимости испытаний не выполняется. Однако пользователя редко интересует устройство программы, для него важно лишь одно: выполняет ли она требуемые функции, поэтому у пользователя нет оснований считать запуски зависимыми. Если же имеется желание использовать информацию об устройстве программы при оценке ее надежности, то следует придумать какую-то более сложную вероятностную модель, которая бы ее учитывала.

Некоторые следствия

Формула (3) позволяет оценить надежность программы по результатам ее запусков. Следует особо остановиться на двух предельных случаях: k = n (нулевая надежность) и k = 0 (абсолютная надежность). В обоих случаях результаты не следует интерпретировать буквально: нет никаких гарантий того, что очередной запуск приведет к тому же реультату, что и предыдущие.

Однако с точки зрения пользователя эти случаи совершенно разные. Если нулевая надежность свидетельствует о том, что программа явно непригодна для эксплуатации, то показатель абсолютной надежности не должен вводить в заблуждение: такой вывод нельзя делать по результатам даже очень большого числа запусков. Следует подчеркнуть, что для оценки надежности в этом случае необходимо рассмотреть другие вероятностные модели.

Из формулы (3) следует, что оценка надежности программы растет с увеличением числа ее запусков по гиперболическому закону. Это подтверждает интуитивно ясное соображение о том, что программа тем надежнее, чем больше опыт ее эксплуатации, который зависит как от интенсивности использования программы, так и от тиража компьютера, на котором она запускается. Таким образом, надежность программ для персональных компьютеров типа IBM РС, общий тираж которых составляет в настоящее время около 100 миллионов, на несколько порядков выше аналогичных программ для специализированных процессоров (если, конечно, такие программы действительно существуют и эксплуатируются).

Стало классическим утверждение, что ошибка в программе обходится тем дороже, чем позже она обнаружена. На самом же деле дорого обходится не ошибка, а опыт эксплуатации программы (т.е. общее количество ее запусков), независимо от того, проявились ошибки или нет. Перед пользователем программы, в которо проявились ошибки, возникает дилемма: продолжать ее эксплуатировать или установить модифицированную версию (разумеется, речь не идет о тех случаях, когда последствия ошибок могут быть катастрофическими). Следует еще раз подчеркнуть, что если программа подвергалась модификациям (в частности, в ней исправлялись ошибки), то при оценке надежности следует учитывать только запуски, выполненные с момента последней модификации: в результате модификации получается новая программа, с другим (возможно, худшим) показателем надежности, и вся прежняя статистика должна быть аннулирована. Этим частично объясняется тот факт, что пользователи порой предпочитают обновленным версиям программ старые, проверенные, эксплуатировавшиеся длительное время, даже если в них обнаружены погрешности: опыт эксплуатации стоит очень дорого, и даже если в программе выявлены ошибки, гораздо дешевле внести исправления и дополнения в инструкции к программе (если это, конечно, возможно), чем пожертвовать накопленным опытом.

Стремление разработчиков создавать бинарно совместимые семейства микропроцессоров находит дополнительное объяснение с позиций надежности программного обеспечения: если бы это удалось в полной мере, то опыт эксплуатации программ не приходилось бы аннулировать при переходе на новый тип процессора, что способствовало бы существенному повышению надежности использующихся программ.

Интересно сравнить характеристики надежности аппаратуры и компьютерной программы. Как известно, надежность физического устройства меняется со временем: в начале эксплуатации она растет (присходит «приработка» изделия), затем некоторое время остается постоянной и, наконец, начинает уменьшаться (эффект износа или «старения»). Говоря о надежности аппаратуры, имеют в виду именно среднюю фазу, на которой надежность постоянна. Всеми отмечается тот факт, что компьютерная программа не изнашивается, так что последней фазы для нее не существует, однако важно подчеркнуть, что первая фаза («приработки» программы) тоже отсутствует: коррекция программы (независимо от причин, по которым она выполнялась) аналогична внесению изменений в конструкцию физического устройства, в результате чего получается новое устройство, с другим показателем надежности.

Несмотря на очевидную актуальность, вопрос оценки надежности программного обеспечения не привлекает должного внимания. Вместе с тем, даже поверхностный анализ проблемы с теоретико-вероятностной точки зрения позволяет выявить некоторые закономерности.

В заключение автор выражает глубокую признательность сотруднику математического отдела НИИСИ РАН А.В. Коганову за весьма полезные дискуссии, а также надежду, что затронутый вопрос заинтересует читателей журнала.

Литература

1. Г. Майерс. Надежность программного обеспечения. Москва, Мир, 1980.

2. Р. Гласс. Руководоство по надежному программированию. Москва, Финансы и статистика, 1982.

3. В. Турский. Методология программирования. Москва, Мир, 1981.

4. В. Феллер. Введение в теорию вероятностей и ее приложения. Т.1. Москва, Мир, 1967

* Отметим, что последовательность испытаний Бернулли — не единственная возможная формализация описываемого процесса. Кроме того, при более пристальном анализе нельзя не обнаружить, что k является функцией n. Тем не менее, даже эта модель дает хорошие качественные результаты. Более тонкие модели заинтересовавшийся читатель сможет найти в статье А. Коганова и С. Романюка «Экономический подход к понятию надежности», которая будет помещена в следующем номере журнала (прим. ред.)

Источник: www.osp.ru

Оценка надежности программ на ранних стадиях проектирования

Оценка надежности ПО по наработке (модель Шумана). Для прогнозирования надежности ПО в этой модели используются данные о числе ошибок, устраненных в процессе компоновки программ в систему ПО и отладки программ. По этим данным вычисляются параметры модели надежности, которая может быть использована для прогнозирования показателя надежности в процессе использования ПО.

Модель основана на следующих допущениях:

— при последовательных прогонах программы наборы входных данных являются случайными и выбираются в соответствии с законом распределения, соответствующим реальным условиям функционирования;

— в начальный момент компоновки программ в систему ПО в них имеется Е0 ошибок; в ходе корректировок новые ошибки не вносятся;

— общее число I машинных команд в программах постоянно, т.е. I=const;

— интенсивность отказов программы пропорциональна числу ошибок, оставшихся в ней после отладки в течение времени , т.е.

где отношение числа ошибок, устраненных в течение времени отладки , к общему числу команд на машинном языке.

Таким образом, в модели различаются два значения времени: время отладки (обычно измеряется месяцами) и время работы программы — суммарная наработка программы (часы и доли часа). Время отладки включает затраты времени на выявление ошибок с помощью тестов, контрольные проверки и т. п. Время исправного функционирования при этом не учитывается.

Таким образом, значение интенсивности отказов считается постоянным в течение всего времени функционирования (0, t). Значение изменяется лишь при обнаружении и исправлении ошибок (при этом время вновь отсчитывается от нуля).

В силу принятых допущений для фиксированного вероятность отсутствия ошибок программ в течение наработки времени (0,t):

Средняя наработка программы до отказа

Для практического использования формулы (2.26) и (2.25) необходимо оценить и по экспериментальным данным. Для этого можно использовать метод моментов или метод максимального правдоподобия.

Применяя метод моментов и рассматривая два периода отладки программ и при

где — продолжительность работы системы, соответствующие и ; и — число ошибок в ПО, обнаруженных соответственно в периодах и .

Оценка надежности программ по числу прогонов (модель Нельсона). В такой модели за показатель надежности программы принимается вероятность безотказного выполнения n прогонов программы.

Вероятность того, что j – й прогон закончится отказом,

где — вероятность выбора i -ого набора входных данных при j – м прогоне некоторой последовательности прогонов; — «динамическая переменная», принимающая значение 0, если прогон программы при i – м наборе входных данных оказывается успешным, и значение 1, если этот прогон заканчивается отказом; N – число возможных наборов входных данных.

На практике надежность программы может быть оценена путем прогона программы на n наборах входных данных и вычисления значения оценки

где — число наборов входных данных, при которых произошли отказы.

Для получения вначале находят «функциональный разрез» программы, т. е. множество вероятностей того, что будет сделан выбор i –ого варианта входных данных. Для этого разбивают все пространство входных переменных на подпространства и находят вероятности того, что выбранный набор входных данных будет принадлежать конкретному подпространству. Это можно сделать, оценивая вероятности появления различных входов в реальных условиях функционирования, для которых оценивается надежность программы.

Далее формируют случайную выборку из n наборов входных данных, распределенных в соответствии с (например, с помощью датчика случайных чисел), и проводят n прогонов программы, находят и вычисляют .

Чтобы установить связь между моделями по наработке и по прогонам, запишем

Описанные выше модели надежности программ требуют оценки ряда параметров по статистическим данным, получаемым при тестировании, отладке программ или на этапе передачи программ в эксплуатацию [12]. На ранних этапах проектирования программ отсутствует возможность проведения экспериментов, могут быть использованы статистические данные об отказах аналогичных программ, созданных ранее той же группой программистов. Рядом исследователей выявлена стабильность относительной частоты ошибок в различных типовых конструкциях алгоритмических языков высокого уровня. Рассмотрим модель надежности программы, основанную на этом явлении и учитывающую структуру программы и распределение исходных данных.

В этой модели предполагается, что:

а) исходные данные выбираются случайно в соответствии имеющимся распределением их вероятностей;

б) ошибки в элементах программы независимы;

в) программа образована из элементов немногих s классов с одинаковыми вероятностями pl правильного однократного исполнения элементов класса l.

При этих допущениях условная вероятность pi правильного однократного пути исполнения программы при условии исполнения пути i:

где mli – количество элементов l – ого класса в i — ом пути. (Путь – последовательность элементов программы, не содержащая ответвлений и используемая при выполнении программы с определенными исходными данными.)

Вероятность правильного однократного исполнения всей программы

где — вероятность выбора i -ого пути (зависит от сочетания значений исходных данных).

Если программа в процессе эксплуатации не корректируется, т. е. проявившиеся ошибки не устраняются, вероятности pi неизменны. При корректировании программ вероятность правильного однократного исполнения элемента l — го класса в период между (j-1) – й и j — й ошибками

где — вероятность правильного однократного исполнения элемента l — го класса до начала эксплуатации или отладки программы; ql – параметр эффективности корректировки (показывает, во сколько раз изменяется вероятность появления ошибки в элементе l – ого класса после ее устранения).

При одинаковых ql=q вероятность правильного однократного исполнения всей программы между (j-1) и j – м отказами

где pсо — вероятность правильного однократного исполнения программы до начала ее эксплуатации или отладки.

Если программа не корректируется после обнаружения в ней ошибок, q=1. Если корректировки неудачны, например, из-за плохого знания программы, q>1. При 0 корректировки повышают надежность программы.

Источник: studopedia.su

Проверка надежности

НАДЕЖНОСТЬ ИСПЫТАНИЯ — это тип тестирования программного обеспечения, который проверяет, может ли программное обеспечение выполнять безотказную работу в течение определенного периода времени в конкретной среде.

Надежность означает «приносить то же самое», другими словами, слово «надежный» означает, что что-то является надежным и что оно каждый раз будет давать один и тот же результат. То же самое верно для тестирования надежности. Проверка надежности программного обеспечения гарантирует, что продукт не имеет ошибок и является надежным по своему назначению.

В этом уроке вы узнаете

• Что такое проверка надежности?
• Пример тестирования надежности
• Факторы, влияющие на надежность программного обеспечения
• Зачем проводить тестирование надежности
• Типы тестирования надежности
• Как сделать тестирование надежности
• Примеры методов проверки надежности
• Инструменты тестирования надежности

Пример тестирования надежности

Вероятность того, что ПК в магазине работает и работает в течение восьми часов без сбоев, составляет 99%; это называется надежностью.

Тестирование надежности можно разделить на три сегмента,

• моделирование
• измерение
• улучшение

Следующая формула предназначена для расчета вероятности отказа.

Probability = Number of failing cases/ Total number of cases under consideration

Факторы, влияющие на надежность программного обеспечения

1. Количество неисправностей, представленных в программном обеспечении
2. Как пользователи работают с системой

• Проверка надежности является одним из ключей к повышению качества программного обеспечения. Это тестирование помогает обнаружить много проблем в дизайне и функциональности программного обеспечения.
• Основная цель проверки надежности состоит в том, чтобы проверить, соответствует ли программное обеспечение требованию надежности клиента.
• Проверка надежности будет проводиться на нескольких уровнях. Сложные системы будут тестироваться на уровне блоков, сборок, подсистем и систем.

Зачем проводить тестирование надежности

Проверка надежности проводится для проверки работоспособности программного обеспечения в данных условиях.

Целью проведения проверки надежности являются:

1. Найти структуру повторяющихся неудач.
2. Для нахождения количества возникающих сбоев указывается указанное количество времени.
3. Раскрыть основную причину отказа
4. Провести тестирование производительности различных модулей программного приложения после устранения дефекта

После выпуска продукта мы также можем минимизировать вероятность появления дефектов и тем самым повысить надежность программного обеспечения. Вот некоторые из инструментов, полезных для этого: анализ тенденций, классификация ортогональных дефектов, формальные методы и т. Д.

Типы тестирования надежности

Тестирование надежности программного обеспечения включает тестирование функций, нагрузочное тестирование и регрессионное тестирование.

Тестирование функций: —

Рекомендуемое тестирование проверяет функцию, предоставляемую программным обеспечением и проводится в следующие шаги:

• Каждая операция в программном обеспечении выполняется как минимум один раз.
• Взаимодействие между двумя операциями уменьшается.
• Каждая операция должна быть проверена на правильность выполнения.

Нагрузочное тестирование: —

Обычно программное обеспечение будет работать лучше в начале процесса, а после этого оно начнет деградировать. Нагрузочное тестирование проводится для проверки производительности программного обеспечения при максимальной рабочей нагрузке.

Регрессионный тест:-

Регрессионное тестирование в основном используется для проверки наличия новых ошибок из-за исправления предыдущих ошибок. Регрессионное тестирование проводится после каждого изменения или обновления функций программного обеспечения и их функций.

Как сделать тестирование надежности

Проверка надежности обходится дороже по сравнению с другими видами тестирования. Поэтому при тестировании надежности необходимо правильное планирование и управление. Это включает в себя процесс тестирования, который будет реализован, данные для среды тестирования, расписание испытаний, точки тестирования и т. Д.

Чтобы начать тестирование на надежность, тестер должен придерживаться следующих вещей,

• Установить цели надежности
• Разработать операционный профиль
• Планируйте и выполняйте тесты
• Используйте результаты тестов для принятия решений

Как мы уже говорили ранее, есть три категории, в которых мы можем проводить тестирование надежности: моделирование, измерение и улучшение .

Ключевые параметры, вовлеченные в тестирование надежности:

• Вероятность безотказной работы
• Продолжительность безотказной работы
• Среда, в которой он выполняется

Шаг 1) Моделирование

Метод моделирования программного обеспечения можно разделить на две подкатегории:

1. Моделирование прогноза

2. Оценочное моделирование

• Значимые результаты могут быть получены путем применения подходящих моделей.
• Допущения и абстракции могут быть сделаны для упрощения проблем, и ни одна модель не подходит для всех ситуаций. Основные отличия двух моделей:

Шаг 2) Измерение

Надежность программного обеспечения не может быть измерена напрямую, и, следовательно, другие связанные факторы учитываются для оценки надежности программного обеспечения. Текущая практика измерения надежности программного обеспечения разделена на четыре категории:

1. Метрики продукта: —

Метрики продукта представляют собой комбинацию 4 типов метрик:

• Размер программного обеспечения : — Линия кода (LOC) — это интуитивно понятный начальный подход к измерению размера программного обеспечения. В этом метрике учитывается только исходный код, а комментарии и другие неисполняемые операторы не учитываются.
• Метрика точки функции : — Метрика функции Pont — это метод измерения функциональности разработки программного обеспечения. Он будет учитывать количество входов, выходов, основных файлов и т. Д. Он измеряет функциональность, предоставляемую пользователю, и не зависит от языка программирования.
• Сложность : — Это напрямую связано с надежностью программного обеспечения, поэтому важно представлять сложность. Метрика, ориентированная на сложность, представляет собой метод определения сложности структуры управления программой путем упрощения кода в графическом представлении.
• Метрики покрытия тестирования : — Это способ оценки неисправности и надежности путем выполнения полного тестирования программных продуктов. Надежность программного обеспечения означает, что это функция определения того, что система была полностью проверена и протестирована.

2. Метрики управления проектом

• Исследователи поняли, что хорошее управление может привести к получению более качественных продуктов.
• Хорошее управление может обеспечить более высокую надежность благодаря использованию лучшего процесса разработки, процесса управления рисками, процесса управления конфигурацией и т. Д.

3. Метрики процесса

Качество продукта напрямую связано с процессом. Метрики процесса могут использоваться для оценки, мониторинга и повышения надежности и качества программного обеспечения.

4. Показатели неисправностей и отказов

Метрики неисправностей и отказов в основном используются для проверки того, является ли система полностью безошибочной. Для достижения этой цели собираются, обобщаются и анализируются как типы ошибок, обнаруженных в процессе тестирования (т. Е. Перед доставкой), так и ошибки, о которых пользователи сообщают после доставки.

Надежность программного обеспечения измеряется в терминах среднего времени наработки на отказ (MTBF) . MTBF состоит из

• Среднее до отказа (MTTF): это разница во времени между двумя последовательными сбоями
• Среднее время ремонта (MTTR): это время, необходимое для устранения неисправности.

MTBF = MTTF + MTTR

Надежность для хорошего программного обеспечения — это число от 0 до 1.

Надежность возрастает при удалении ошибок или ошибок из программы.

Шаг 3) Улучшение

Улучшение полностью зависит от проблем, возникших в приложении или системе, или от характеристик программного обеспечения. В зависимости от сложности программного модуля, путь улучшения также будет отличаться. Два основных ограничения времени и бюджета, которые ограничат усилия, вкладываются в повышение надежности программного обеспечения.

Примеры методов проверки надежности

Тестирование на надежность подразумевает выполнение приложения таким образом, чтобы сбои обнаруживались и устранялись до развертывания системы.

В основном, для тестирования надежности используются три подхода

• Тест-ретест Надежность
• Надежность параллельных форм
• Согласованность решений

Ниже мы попытались объяснить все это на примере.

Тест-ретест Надежность

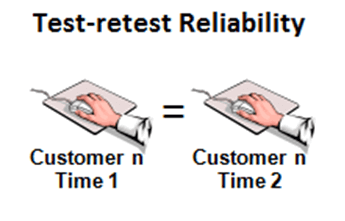
Чтобы оценить надежность тест-повторного тестирования, одна группа испытуемых выполнит процесс тестирования с интервалом в несколько дней или недель. Время должно быть достаточно коротким, чтобы можно было оценить навыки испытуемых в этой области. Соотношение между баллами испытуемого от двух разных администраций оценивается посредством статистической корреляции. Этот тип надежности демонстрирует степень, в которой тест способен производить стабильные, согласованные оценки во времени.

Надежность параллельных форм

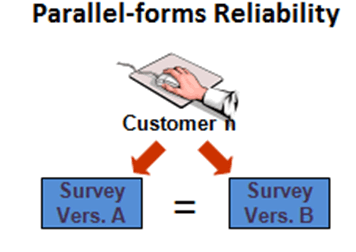
Многие экзамены имеют несколько форматов вопросов, эти параллельные формы экзамена обеспечивают безопасность. Надежность параллельных форм оценивается путем предоставления обеих форм экзамена одной и той же группе испытуемых. Баллы испытуемых по двум тестовым формам коррелируют, чтобы определить, как одинаково функционируют две тестовые формы. Эта оценка достоверности является мерой того, насколько единообразные оценки испытуемых можно ожидать в разных формах теста.

Согласованность решений

После выполнения тест-повторной проверки надежности и надежности параллельной формы, мы получим результат экзаменующихся, как пройденных, так и неуспешных. Именно надежность этого классификационного решения оценивается в надежности согласованности решений.

Важность тестирования надежности

Тщательная оценка надежности необходима для повышения производительности программного продукта и процесса. Тестирование надежности программного обеспечения поможет руководителям и практикам программного обеспечения в значительной степени.

Чтобы проверить надежность программного обеспечения с помощью тестирования: —

1. Большое количество тестовых случаев должно быть выполнено в течение длительного периода времени, чтобы выяснить, как долго программа будет работать без сбоев.
2. Распределение тестовых случаев должно соответствовать фактическому или запланированному рабочему профилю программного обеспечения. Чем чаще выполняется функция программного обеспечения, тем больше процент тестовых случаев, которые должны быть выделены для этой функции или подмножества.

Инструменты тестирования надежности

Некоторые из инструментов, используемых для надежности программного обеспечения, являются

1. WEIBULL ++: — Анализ данных о сроке службы

2. RGA: — Анализ роста надежности

3. RCM: -обслуживание, ориентированное на надежность

Summary:

Reliability Testing is the important part of a reliability engineering program. More correctly, it is the soul of reliability engineering program.

Furthermore, reliability tests are mainly designed to uncover particular failure modes and other problems during software testing.

In Software Engineering, Reliability Testing can be categorized into three segments,

• Modeling
• Measurement
• Improvement

Factors Influencing Software Reliability

• The number of faults presents in the software
• The way users operate the system

Источник: coderlessons.com