Мезоцикл — это средний тренировочный цикл продолжительностью от 2 до 6 недель, включающий относительно законченный ряд микроциклов.
Построение тренировочного процесса на основе мезоциклов позволяет систематизировать его в соответствии с главной задачей периода или этапа подготовки, обеспечить оптимальную динамику тренировочных и соревновательных нагрузок, целесообразное сочетание различных средств и методов подготовки, соответствие между факторами педагогического воздействия и восстановительными мероприятиями, достичь преемственности в вос-Шитании различных качеств и способностей.
Внешними признаками мезоцикла являются: 1) повторное воспроизведение ряда микроциклов (обычно однородных) в единой последовательности либо чередование различных микроциклов в определенной последовательности. При этом в подготовительном периоде они чаще повторяются, а в соревновательном, чаще чередуются; 2) смена одной направленности микроциклов другими характеризует и смену мезоцикла; 3) заканчивается мезоцикл восстановительным (разгрузочным) микроциклом, соревнованиями или контрольными испытаниями.
«Организация лечебного питания в ЛПУ»
Анализ тренировочного процесса в различных видах спорта позволяет выделить определенное число типовых мезоциклов: втягивающих, базовых, контрольно-подготовительных, предсорев-новательных, соревновательных, восстановительных.
Втягивающие мезоциклы. Их основная задача — постепенное подведение спортсменов к эффективному выполнению специфической тренировочной работы. Это обеспечивается применением упражнений, направленных на повышение или восстановление работоспособности систем и механизмов, определяющих уровень разных компонентов выносливости; скоростно-силовых качеств и гибкости; становление двигательных навыков и умений. Эти мезоциклы применяются в начале сезона, после болезни или травм, а также после других вынужденных или запланированных перерывов в тренировочном процессе.
Базовые мезоциклы. В них планируется основная работу по повышению функциональных возможностей основных систем организма, совершенствованию физической, технической, тактической и психической подготовленности. Тренировочная программа характеризуется использованием всей совокупности средств, большой по объему и интенсивности тренировочной работой, широким использованием занятий с большими нагрузками. Базовые мезоциклы составляют основу подготовительного периода, а в соревновательный включаются с целью восстановления физических качеств и навыков, утраченных в ходе стартов.
Контрольно-подготовительные мезоциклы. Характерной особенностью тренировочного процесса в этих мезоциклах является широкое применение соревновательных и специально подготовительных упражнений, максимально приближенных к соревновательным. Эти мезоциклы характеризуются, как правило, высокой интенсивностью тренировочной нагрузки, соответствующей соревновательной или приближенной к ней. Они используются во второй половине подготовительного периода и в соревновательном периоде как промежуточные мезоциклы между напряженными стартами, если для этого имеется соответствующее время.
Идеальные Отношения: 3 Принципа. Признаки здоровых и больных отношений
Предсоревновательные (подводящие) мезоциклы предназначены для окончательного становления спортивной формы за счет устранения отдельных недостатков, выявленных в ходе подготовки
спортсмена, совершенствования его технических возможностей. |
Особое место в этих мезоциклах занимает целенаправленная психическая и тактическая подготовка. Важное место отводится моделированию режима предстоящего соревнования.
Общая тенденция динамики нагрузок в этих мезоциклах характеризуется, как правило, постепенным снижением суммарного объема и объема интенсивных средств тренировки перед главными соревнованиями. Это связано с существованием в организме механизма «запаздывающей трансформации» кумулятивного эффекта тренировки, который состоит в том, что пик спортивных достижений как бы отстает по времени от пиков общего и частных наиболее интенсивных объемов нагрузки. Эти мезоциклы характерны для этапа непосредственной подготовки к главному старту и имеют важное значение при переезде спортсменов в новые контрастные климато-географические условия.
Соревновательные мезоциклы. Их структура определяется спецификой вида спорта, особенностями спортивного календаря, квалификацией и уровнем подготовленности спортсмена. В большинстве видов спорта соревнования проводятся в течение всего года на протяжении 5—10 месяцев. В течение этого времени может проводиться несколько соревновательных мезоциклов.
В простейших случаях мезоциклы данного типа состоят из одного подводящего и одного соревновательного микроциклов. В этих мезоциклах увеличен объем соревновательных упражнений.
Восстановительный мезоцикл составляет основу переходного периода и организуется специально после напряженной серии соревнований. В отдельных случаях в процессе этого мезоцикла возможно использование упражнений, направленных на устранение проявившихся недостатков или подтягивание физических способностей, не являющихся главными для данного вида спорта. Объем соревновательных и специально подготовительных упражнений значительно снижается.
Источник: fkis.ru
Метрики сложности программ
При оценке сложности программ, как правило, выделяют три основные группы метрик: метрики размера программ, метрики сложности потока управления программ и метрики сложности потока данных программ.
Оценки первой группы наиболее просты и поэтому получили широкое распространение. Традиционной характеристикой размера программ является количество строк исходного текста. Под строкой понимается любой оператор программы.
Непосредственное измерение размера программы, несмотря на свою простоту, дает хорошие результаты. Оценка размера программы недостаточна для принятия решения о ее сложности. Но вполне применима для классификации программ, существенно различающихся объемами. При уменьшении различий в объеме программ на первый план выдвигаются оценки других факторов, оказывающих влияние на сложность. Таким образом, оценка размера программы есть оценка по номинальной шкале, на основе которой определяются только категории программ без уточнения оценки для каждой категории.
К группе оценок размера программ можно отнести также метрику Холстеда. За базу принят подсчет количества операторов и операндов используемых в программе, т.е. определение размера программы.
Основу метрики Холстеда составляют четыре измеряемые характеристики программы: h1 — число уникальных операторов программы, включая символы-разделители, имена процедур и знаки операций (словарь операторов); h2 – число уникальных операндов программы (словарь операндов); N1 – общее число операторов в программе N2 – общее число операндов в программе.
Опираясь на эти характеристики, получаемые непосредственно при анализе исходных текстов программ, Холстед вводит следующие оценки
Словарь программы h=h1 + h2
Длину программы N=N1+N2
Объем программы V=N log2 h
Смысл оценок h и N достаточно очевиден, поэтому подробно рассмотрим только характеристику V.
Количество символов, используемых при реализации некоторого алгоритма, определяется в числе прочих параметров и словарей программы h, представляющим собой минимально необходимое число символов, обеспечивающих реализацию алгоритма.
Далее Холстед вводит h* — теоретический словарь программы, т.е. словарный запас, необходимый для написания программы с учетом того, что необходимая функция уже реализована в данном языке и, следовательно, программа сводится к вызову этой функции. Например, согласно Холстеду возможное осуществление процедуры выделения простого числа могло бы выглядеть так:
CALL SIMPLE (X, Y),
где Y- массив численных значений, содержащих искомое число X.
Теоретический словарь в этом случае будет состоять из
а его длина, определяемая как
h* = h1* + h2* будет равна 4.
Используя h*, Холстед вводит оценку V*: V* = h*log2h*,
с помощью которой описывается потенциальный объем программы, соответствующий максимально компактно реализующей данный алгоритм.
Вторая наиболее представительная группа оценок сложности программ – метрики сложности потока управления программ. Как правило, с помощью этих оценок оперируют либо плотностью управляющих переходов внутри программ, либо взаимосвязями этих переходов.
И в том и в другом случае стало традиционным представление программ в виде управляющего ориентированного графа G(V,E), где V – вершины, соответствующие операторам, а E – дуги, соответствующие переходам. В дуге (U,V) – вершина V является исходной, а U – конечной. При этом U непосредственно следует V, а V непосредственно предшествует U. Если путь от V до U состоит более чем из одной дуги, тогда U следует за V, а V предшествует U.
Впервые графическое представление программ было предложено Маккейбом. Основной метрикой сложности он предлагает считать цикломатическую сложность графа программы, или, как еще называют, цикломатическое число Маккейба, характеризующее трудоемкость тестирования программы.
Для вычисления цикломатического числа Маккейба Z(G) применяется формула
где l – число дуг ориентированного графа G; v – число вершин; p- число компонентов связности графа.
Число компонентов связности графа можно рассматривать как количество дуг, которые необходимо добавить для преобразования графа сильносвязный. Сильносвязным называется граф, любые две вершины которого взаимно достижимы. Для графов корректных программ, т.е. графов, не имеющих недостижимых от точек входа участков и “висячих” входа и выхода, сильносвязный граф, как правило, получается путем замыкания одной вершины, обозначающей конец программы на вершину, обозначающую точку входа в эту программу.
По сути Z(G) определяет число линейно независимых контуров в сильносвязном графе. Иначе говоря, цикломатическое число Маккейба показывает требуемое число проходов для покрытия всех контуров сильносвязанного графа или количество тестовых прогонов программы, необходимых для исчерпывающего тестирования по критерию “работает каждая ветвь”.






Для программы цикломатическое число при l=10, v=8, n=1 определится как Z(G) = 10-8+2=4.
Таким образом, имеется сильносвязанный граф с четырьмя линейно независимыми контурами:
Рассмотрим метрику сложности программы, получившую название “подсчет точек пересечения”, авторами которой являются М Вудвард, М Хенел и Д Хидлей. Метрика ориентирована на анализ программ, при создании которых использовалось неструктурное кодирование на таких языках, как язык ассемблера и фортран. Вводя эту метрику, ее авторы стремились оценить взаимосвязи между физическими местоположениями управляющих переходов.
Структурное кодирование предполагает использование ограниченного множества управляющих структур в качестве первичных элементов любой программы. В классическом структурном кодировании, базирующемся на работах профессора Эйндховенского технологического университета(Нидерланды) Э. Дейкстры, оперируют только тремя такими структурами: следованием операторов, развилкой из операторов, циклом над оператором. все эти разновидности изображаются простейшими планарными графами программ. По правилам структурного кодирования любая программа составляется путем выстраивания цепочек из 3х упомянутых структур или помещения одной структуры в другую. Эти операции не нарушают планарности графа всей программы.
В графе программы, где каждому оператору соответствует вершина, т.е. не исключены линейные участки , при передаче управления от вершины a к b номер оператора a равен min (a,b), а номер оператора b — max(a,b). Тогда пересечение дуг появятся, если
Иными словами, точка пересечения дуг возникает в случае выхода управления за пределы пары вершин (a,b).
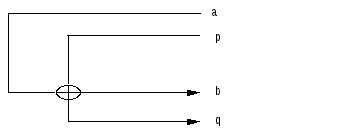
Количество точек пересечения дуг графа программы дает характеристику
Одной из наиболее простых, но достаточно эффективных оценок сложности программ является метрика Т. Джилба, в которой логическая сложность программы определяется как насыщенность программы выражениями IF_THEN_ELSE. При этом вводятся две характеристики:
- СL — абсолютная сложность программы, характеризующаяся количеством операторов условия;
- cl — относительная сложность программы, характеризующаяся насыщенностью программы операторами условия, т.е. cl определяется как отношение CL к общему числу операторов.
Используя метрику Джилба, ее дополнили еще одной составляющей, а именно характеристикой максимального уровня вложенности оператора CLI, что позволило применить метрику Джилба к анализу циклических конструкций. Большой интерес представляет оценка сложности программ по методу граничных значений. Введем несколько дополнительных понятий, связанных с графом программы. Пусть G=(V,E) — ориентированный граф программы с единственной начальной и единственной конечной вершинами. В этом графе число входящих в вершину дуг называется отрицательной степенью вершины, а число исходящих из вершины дуг — положительной степенью вершины. Тогда набор вершин графа можно разбить на две группы:
- вершины у которых положительная степень
- вершины у которых положительная степень >=2.
Вершины первой группы назовем принимающими вершинами, а вершины второй группы — вершинами отбора. Для получения оценки по методу граничных значений необходимо разбить граф G на максимальное число подграфов G’, удовлетворяющих следующим условиям:
- вход в подграф осуществляется только через вершину отбора;
- каждый подграф включает вершину (называемую нижней границей подграфа), в которую можно попасть из любой другой вершины подграфа. Например, вершина отбора соединенная сама с собой дугой петлей, образует подграф.









 Число вершин, образующих такой подграф, равно скорректированной сложности вершины отбора:
Число вершин, образующих такой подграф, равно скорректированной сложности вершины отбора:
| Характеристикиподграфов программ | Вершины отбора | |||
| a | b | c | d | |
| Вершины перехода | b,c | b,d | e,f | g,h |
| Скорректированная сложность вершины графа | 10 | 2 | 3 | 3 |
| Вершины подграфа | b,c,d, e,f,g, h,i,j | b | l,j | g,h |
| Нижняя граница подграфа | k | d | i | j |
Каждая принимающая вершина имеет скорректированную сложность, равную 1, кроме конечной вершины, скорректированная сложность которой равна 0. Скорректированные сложности всех вершин графа G суммируются, образуя абсолютную граничную сложность программы. После этого определяется относительная граничная сложность программы: S0=1-(v-1)/Sa, где S0 – относительная граничная сложность программы; Sa – абсолютная граничная сложность программы, v – общее число вершин графа программы. Таким образом, относительная сложность программы равна S0=1-(11/25)=0,56. Другая группа метрик сложности программ – метрика сложности потока данных, то есть использования, конфигурации и размещения данных в программах. Пара “модуль – глобальная переменная” обозначается как (p,r), где p – модуль, имеющий доступ к глобальной переменной r. В зависимости от наличия в программе реального обращения к переменной r формируются два типа пар “модуль – глобальная переменная” : фактические и возможные. Возможное обращение к r с помощью p показывает, что область существования r включает в себя p. Характеристика Aup говорит о том, сколько раз модули Up действительно получили доступ к глобальным переменным, а число Pup – сколько раз они могли бы получить доступ. Отношение числа фактических обращений к возможным определяется Rup=Aup/Pup Эта формула показывает приближенную вероятность ссылки произвольного модуля на произвольную глобальную переменную. Очевидно, чем выше эта вероятность, тем выше вероятность “несанкционированного” изменения какой-либо переменной, что может существенно осложнить работы, связанные с модификацией программы. Покажем расчет метрики “модуль – глобальная переменная”. Пусть в программе имеются три глобальные переменные и три подпрограммы. Если предположить, что каждая подпрограмма имеет доступ к каждой из переменных, то мы получим девять возможных пар, то есть Pup=9. Далее пусть первая подпрограмма обращается к одной переменной, вторая – двум, а третья не обращается ни к одной переменной. Тогда Aup=3, Rup=3/9. Еще одна метрика сложности потока данных – спен. Определение спена основывается на локализации обращения к данным внутри каждой программной секции. Спен – это число утверждений, содержащих данный идентификатор, между его первым и последним появлением в тексте программы. Идентификатор, появившийся n раз, имеет спен, равный n-1. Спен определяет количество контролирующих утверждений, вводимых в тело программы при построении трассы программы по этому идентификатору в процессе тестирования и отладки. Следующей метрикой сложности потока данных программ является метрика Чепина. Существует несколько ее модификаций. Рассмотрим более простой, а с точки зрения практического использования – достаточно эффективный вариант этой метрики. Суть метода состоит в оценке информационной прочности отдельно взятого программного модуля с помощью анализа характера использования переменных из списка ввода-вывода. Все множество переменных, составляющих список ввода-вывода разбивается на четыре функциональные группы
- Р – вводимые переменные для расчетов и для обеспечения вывода. Примером может служить используемая в программах лексического анализатора переменная, содержащая строку исходного текста программы, то есть сама переменная не модифицируется, а только содержит исходную информацию.
- М – модифицируемые или создаваемые внутри программы переменные.
- C – переменные, участвующие в управлении работой программного модуля (управляющие переменные).
- Не используемые в программе (“паразитные”) переменные. Поскольку каждая переменная может выполнять одновременно несколько функций, необходимо учитывать ее в каждой соответствующей функциональной группе.
Далее вводится значение метрики Чепина: Q = a1P + a2M + a3C + a4T ,где a1, a2, a3, a4 – весовые коэффициенты. Весовые коэффициенты использованы для отражения различного влияния на сложность программы каждой функциональной группы. По мнению автора метрики, наибольший вес, равный трем, имеет функциональная группа С, так как она влияет на поток управления программы. Весовые коэффициенты остальных групп распределяются следующим образом: a1=1; a2=2; a4=0.5. Весовой коэффициент группы T не равен нулю, поскольку “паразитные” переменные не увеличивают сложности потока данных программы, но иногда затрудняют ее понимание. С учетом весовых коэффициентов выражение примет вил: Q = P + 2M + 3C + 0.5T . Следует отметить, что рассмотренные метрики сложности программы основаны на анализе исходных текстов программ, что обеспечивает единый подход к автоматизации их расчета.
Источник: studfile.net
Рабочая программа ВДУ Математическая грамотность 5 класс


Программа внеурочной деятельности для обучающихся 5 класса составлена на основе:
1. Закона «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012г
2. Федерального государственного образовательного стандарта основного общего образования, утв. приказом Минобрнауки России от 17.12.2010 №1897.
3. Основной образовательной программы ООО МБОУ«Кожинская СОШ» на 2018 – 2023 гг
4. Программы «Развитие функциональной грамотности обучающихся основной школы: методическое пособие для педагогов». Под общей редакцией Л.Ю. Панариной, И.В. Сорокиной, О.А. Смагиной, Е.А. Зайцевой. – Самара: СИПКРО, 2019
5. Учебного пособия для общеобразовательных организаций «Математическая грамотность. Сборник эталонных заданий» в 2-х частях. Выпуск 1. Под редакцией Г.С. Ковалевой, Л.О. Рословой, -М., СПб.: Просвещение, 2020
6. PISA: математическая грамотность. – Минск: РИКЗ, 2020. – 252 с.
Понятие функциональной грамотности сравнительно молодо: появилось в конце 60-х годов прошлого века в документах ЮНЕСКО и позднее вошло в обиход исследователей. Примерно до середины 70-х годов концепция и стратегия исследования связывалась с профессиональной деятельностью людей: компенсацией недостающих знаний и умений в этой сфере.
В дальнейшем этот подход был признан односторонним. Функциональная грамотность стала рассматриваться в более широком смысле: включать компьютерную грамотность, политическую, экономическую грамотность и т.д.
В таком контексте функциональная грамотность выступает как способ социальной ориентации личности, интегрирующей связь образования (в первую очередь общего) с многоплановой человеческой деятельностью.
Мониторинговым исследованием качества общего образования, призванным ответить на вопрос: «Обладают ли учащиеся 15-летнего возраста, получившие обязательное общее образование, знаниями и умениями, необходимыми им для полноценного функционирования в современном обществе, т.е. для решения широкого диапазона задач в различных сферах человеческой деятельности, общения и социальных отношений?»11, — является PISA( Programme for International Student Assessment ).
И функциональная грамотность понимается PISA как знания и умения, необходимые для полноценного функционирования человека в современном обществе. PISA в своих мониторингах оценивает 4 вида грамотности: читательскую, математическую, есте-ственнонаучную и финансовую.
Проблема развития функциональной грамотности обучающихся в России актуализировалась в 2018 году благодаря Указу Президента РФ от 7 мая 2018 г. № 204 «О национальных целях и стратегических задачах развития Российской Федерации на период до 2024 года». Согласно Указу, «в 2024 году необходимо обеспечить глобальную конкурентоспособность российского образования, вхождение Российской Федерации в число 10 ведущих стран мира по качеству общего образования».
Поскольку функциональная грамотность понимается как совокупность знаний и умений, обеспечивающих полноценное функционирование человека в современном обществе, ее развитие у школьников необходимо не только для повышения результатов мониторинга PISA, как факта доказательства выполнения Правительством РФ поставленных перед ним Президентом задач, но и для развития российского общества в целом.
Низкий уровень функциональной грамотности подрастающего поколения затрудняет их адаптацию и социализацию в социуме. Современному российскому обществу нужны эффективные граждане, способные максимально реализовать свои потенциальные возможности в трудовой и профессиональной деятельности, и тем самым принести пользу обществу, способствовать развитию страны. Этим объясняется актуальность проблемы развития функциональной грамотности у школьников на уровне общества.
Результаты лонгитюдных исследований, проведенных на выборках 2000 и 2003 гг. странами-участницами мониторингов PISA показали, что результаты оценки функциональной грамотности 15-летних учащихся являются надежным индикатором дальнейшей образовательной траектории молодых людей и их благосостояния. Любой школьник хочет быть социально успешным, его родители также надеются на высокий уровень благополучия своего ребенка во взрослой жизни. Поэтому актуальность развития функциональной грамотности обоснована еще и тем, что субъекты образовательного процесса заинтересованы в высоких академических и социальных достижениях обучающихся, чему способствует их функциональная грамотность.
Программа рассчитана на проведение практических занятий в объёме 35 часов в год, 1 час в неделю.
Результаты освоения учебного курса
Основной целью программы является развитие функциональной грамотности учащихся 8 класса как индикатора качества и эффективности образования, равенства доступа к образованию.
Программа нацелена на развитие:
способности человека формулировать, применять и интерпретировать математику в разнообразных контекстах. Эта способность включает математические рассуждения, использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые необходимы конструктивному, активному и размышляющему гражданину
Метапредметные и предметные
— находить и извлекать математическую информацию в различном контексте
— применять математические знания для решения разного рода проблем
— формулировать математическую проблему на основе анализа ситуации
— интерпретировать и оценивать математические данные в контексте лично значимой ситуации
Личностные результаты
— объяснять гражданскую позицию в конкретных ситуациях общественной жизни на основе математических знаний с позиции норм морали и общечеловеческих ценностей.
Основные виды деятельности обучающихся: самостоятельное чтение и
обсуждение полученной информации с помощью вопросов (беседа, дискуссия, диспут); выполнение практических заданий; поиск и обсуждение материалов в сети Интернет; решение ситуационных и практико-ориентированных задач.
В целях развития познавательной активности обучающихся на занятиях используются деловые и дидактические игры, разрабатываются и реализовываются мини-проекты, организовываются турниры и конкурсы.
Содержание учебного курса
Применение чисел и действий над ними. Счет и десятичная система счисления. Сюжетные задачи, решаемые с конца. Задачи на переливание (задача Пуассона) и взвешивание. Логические задачи: задачи о «мудрецах», о лжецах и тех, кто всегда говорит правду. Первые шаги в геометрии.
Простейшие геометрические фигуры. Наглядная геометрия. Задачи на разрезание и перекраивание. Разбиение объекта на части и составление модели. Размеры объектов окружающего мира (от элементарных частиц до Вселенной) длительность процессов окружающего мира. Числа и единицы измерения: время, деньги, масса, температура, расстояние. Логические задачи, решаемые с помощью таблиц.
Комбинаторные задачи. Представление данных в виде таблиц, диаграмм, графиков.
Формы проведения занятий подбираются с учетом цели и задач, познавательных интересов, индивидуальных возможностей воспитанников:
— тематические задания по подгруппам;
Источник: znanio.ru